Question: Advanced Linear Algebra / Advanced Math / Matlab question need help! Some of the needed codes are attached. In the question, it talks about the
Advanced Linear Algebra / Advanced Math / Matlab question need help!
Some of the needed codes are attached.
In the question, it talks about the HW 6.1 but it can be neglected because every thing needed is in the question.
Maybe it is too hard problem to ask on chegg but I believe that there are some of you who are way smarter than I can ever be.
Hope this can work out...
I am sorry for posting a question like this.



GaussSeidel.m code is below
function [Yhistory,ErrorP,ErrorR,Iter]= GaussSeidel(L,YL,YR,M,tolX,tolR)
% GaussSeidel uses the iterative method to solve for the height Y(x) % for M equally-spaced points of a sagging cable supported at each end. % % INPUTS % L Distance between cable supports (m) % YL, YR Height at left & right ends of cable (m) % M Number of equally-spaced points picked to solve Y(x) % tolX Convergence tolerance for "proxy error" in Y vector (L2 norm) % tolR Convergence tolerance for residual error (L2 norm) % % OUTPUTS % Yhistory Each column of Yhistory will be the height distribution % Y(x) for each Gauss-S iteration. Size: (M) x (# Iterations) % ErrorP Vector (length: Iter) with L2-norm of "Proxy error in X" for % each iteration. For the initial guess, just set ErrorP= NaN. % ErrorR Vector (length: Iter) with L2-norm of "Residual error" for % each iteration. % Iter Total number of iterations it took to converge.
% ** YOU ** need to write and document this entire routine to provide the % required outputs. Key things to remember: % % 1. For your initial guess, pick Y= (YR+YL)/2 for all the elements. % 2. Use a "while loop" to keep iterating until you meet BOTH convergence % criteria. % 3. Make sure the first (left-most) column of Yhistory is your initial % guess. Then each subsequent column (to the right) stores the next % iteration of the Y vector. The very last column in Yhistory would % then be your "final" answer.
%% Create A and b matrices (i.e. Write problem in Ax=b form) A= zeros(M,M); b= zeros(M,1);
A(1,1) = 1; b(1)= YL; % 1st equation (set Y1 to YL = 6 meters)
for i = 2:(M-1) % 2nd through (M-1) equations for all A(i,i-1)= 628.125; % "internal" y points A(i,i)= -1250.1; A(i,i+1)= 621.875; b(i) = 0; end
A(M,M) = 1; b(M)= YR; % Last equation (set YM to YR = 10 meters)
%% First guess and Initialize Yhistory, ErrorP and ErrorR matrices % Initial guess: Assume all heights are just 8 m (avg of 6 and 10) % so create a 251x1 vector of the number "8" as the first guess. Y= ones(M,1) * mean([YL YR]);
% Initialize matrices that will hold Y and Errors for each iteration. k=1; % Iteration number (k --> start at 1) Yhistory= [Y]; ErrorP= [NaN]; ErrorR= [norm(A*Y-b,2)];
%% Gauss-Seidel Iteration % Iterate until L2 norm of BOTH error in x AND residual are below tols. % Save new Y vector, "proxy" error and residual error for each iteration % as a new column in the Yhistory, ErrorP and ErrorR variables. % Don't forget to also set Iter to the final iteration number.
while ... % You do all the rest! Hint: my code only requires a dozen more lines.
HW6_6.m code is below
%%%%%%%%%%%%%%%%% Numerical Methods Homework Problem 6.6 %%%%%%%%%%%%%%%%% % DO NOT change this main script!! Use it exactly as it is!! % % YOU need to make the function GaussSeidel.m to interface with this script % to create the needed outputs which allow the plots at the end to be made.
%% Specify Characteristics of Hanging Cable clear M= 251; % Number of points along cable to calculate Y(x)
L= 10; % Distance between supports (m) YL= 6; % Height of cable at Left suport, (m) YR= 10; % Height of cable at Right support, (m) tolX= 1e-3 * sqrt(M); % Convergence tolerance for "proxy error in X" tolR= 1e-3 * sqrt(M); % Convergence tolerance for residual error
%% Run YOUR Gauss-Seidel Iterative Method [Yhistory, ErrorP, ErrorR, Iter]= GaussSeidel_done(L, YL,YR, M, tolX,tolR);
%% Plot Y(x) from Gauss-Seidel Solution on top of the shape of the hill % Plot lines for k=1, 100, 1000, 5000 and final ("end") iterations. % Shape of Hill will overlay as a dashed black line
x= linspace(0,L,M)'; % M points (x) along cable, from x=0 to x=L
subplot(121); plot(x,Yhistory(:,[1 100 1000 5000 end]), [0 L],[0 4],'--k', 'linewidth',2) grid on; axis([0 L 0 12]) xlabel('x (meters)'); ylabel('Height (meters)') title('Height Profiles During Convergence') legend('1st','100th','1000th','5000th','Final','Hillside', ... 'Location','northwest')
%% Plot convergence history: "proxy" error and residual error vs k % "Proxy" for error in Y is solid BLUE, residual error is dashed RED. subplot(122) plot([1:Iter],log10(ErrorP),'-b', [1:Iter],log10(ErrorR),'--r', ... 'linewidth',2) grid on xlabel('Iteration (k)'); ylabel('log_1_0(Error) (L_2 norm)') title(['Convergence History, Final k = ' num2str(Iter)]) legend('Proxy Error in Y', 'Residual Error')
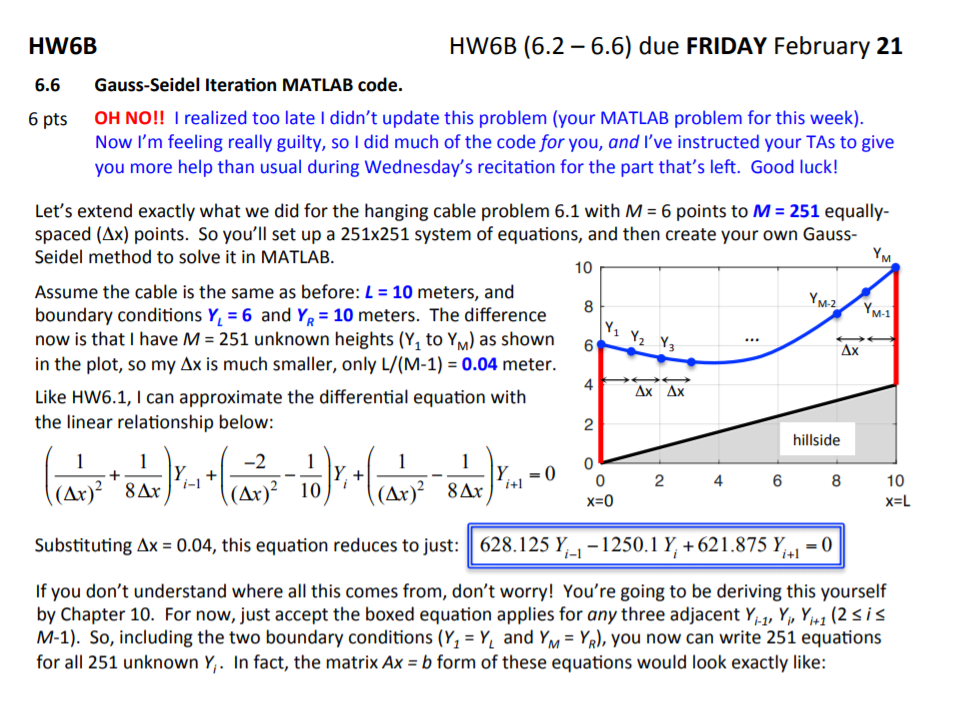
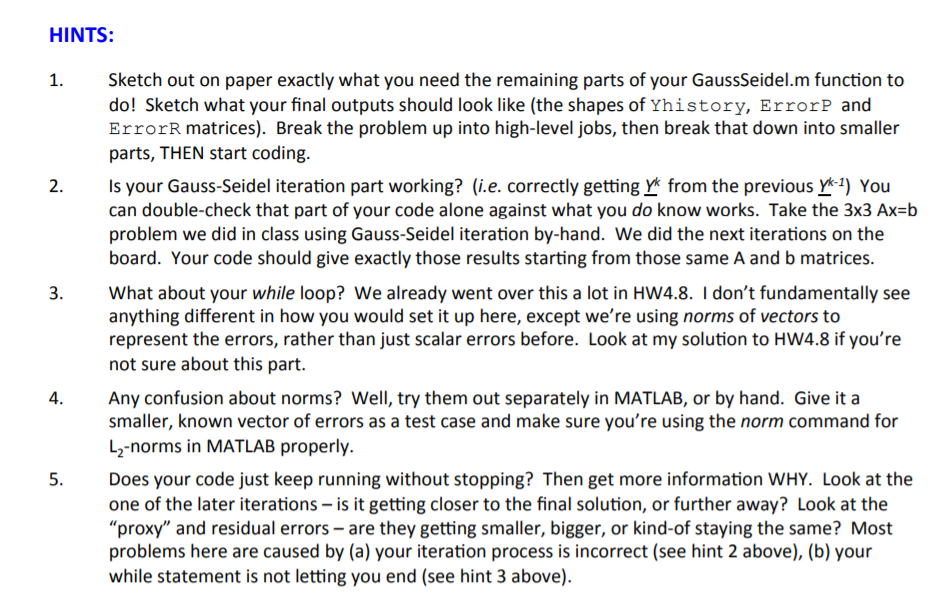
HW6B HW6B (6.2 - 6.6) due FRIDAY February 21 6.6 6 pts Gauss-Seidel Iteration MATLAB code. OH NO!! I realized too late I didn't update this problem (your MATLAB problem for this week). Now I'm feeling really guilty, so I did much of the code for you, and I've instructed your TAs to give you more help than usual during Wednesday's recitation for the part that's left. Good luck! Let's extend exactly what we did for the hanging cable problem 6.1 with M = 6 points to M = 251 equally- spaced (Ax) points. So you'll set up a 251x251 system of equations, and then create your own Gauss- Seidel method to solve it in MATLAB. 10 Y Y2Y3 6 Assume the cable is the same as before: L = 10 meters, and boundary conditions Y = 6 and Y. = 10 meters. The difference now is that I have M = 251 unknown heights (Y, to Ym) as shown in the plot, so my Ax is much smaller, only L/(M-1) = 0.04 meter. Like HW6.1, I can approximate the differential equation with the linear relationship below: >AX AX hillside 1 y +1 = 0 0 2 2 10 4 6 (Ar) 2 8 (A Ar 10 x=L x=0 Substituting Ax = 0.04, this equation reduces to just: 628.125 Y_, -1250.1 Y, +621.875 Y = 0 If you don't understand where all this comes from, don't worry! You're going to be deriving this yourself by Chapter 10. For now, just accept the boxed equation applies for any three adjacent Y:-1, Y, Yi+1 (2 sis M-1). So, including the two boundary conditions (Y = Y, and YM = YR), you now can write 251 equations for all 251 unknown Y. In fact, the matrix Ax = b form of these equations would look exactly like: 628.125 -1250.1 621.875 628.125 -1250.1 621.875 628.125 -1250.1 621.875 628.125 -1250.1 621.875 To solve this I have posted a script HW6_6.m that already does all the following for you: Initializes variables for the cable (L, YU, YR), and M = 251, sets values for convergence tolerances for the L, norm of "proxy" error between iterations and the residual error (tolx = tolr = sqrt(M) x 10-3, using M = 251), calls a (incomplete!) function GaussSeidel.m to iteratively solve for all 251 Y, until convergence, Uses the results from GaussSeidel.m to make two plots: (i) the Y/(x) distribution for the 1st, 100th, 1000th, 5000th and final (converged) iterations compared to the exact solution, and (ii) the logo(error) convergence history. Your job is just to complete the function GaussSeidel.m that's called by the above code. HW6B HW6B (6.2 6.6) due FRIDAY February 21 6.6 Continued ... To help, I've actually already started your function for you. Upload the "code fragment" GaussSeidel.m in this same Carmen assignment. You'll see that I have: Given the 1st line of the function, to ensure compatibility with HW6_6.m. DON'T CHANGE IT!! function (Yhistory, ErrorP, ErrorR, Iter]= Gauss Seidel (L, YL, YR, M, tolx, tolR) Created the the A and b matrices from the last page, to make sure everyone's starting with the correct set of equations. Created the initial guess, Y, as the average value between the poles (Y +YR) = 8 m for all y. (I realize we called the first guess k=0 in class, but it's just a lot easier in this code to call it k=1.) Initialized the Yhistory, ErrorP and ErrorR matrices given that first k=1 guess: I just put the initial guess Y1 as the first column vector in Yhistory. Since we can't calculate a "proxy" error for the first guess (there is no previous iteration to compare it to), I just set the first value of "proxy" error vector Error P to be NaN (not a number"). That way it won't appear on the error plot later. We can calculate a residual error for the first guess, using the Lz-norm of AY -b, so I used that to start the residual error vector ErrorR. Your job is to now complete the function GaussSeidel.m to do the following: a) EXACTLY interfaces with my main script, using all the same inputs and outputs from the 1st line above. b) Calculate the column vector yk for each iteration k> 1 using the Gauss Seidel iterative method. c) Use a "while loop to keep iterating until the Lz-norms of both the "proxy" error between iterations and the residual error are within their tolerances. d) Store each iteration yk as a column vector in the variable Yhistory. So, for example, if you're done after k = 1000 iterations, then Yhistory would be a 251 x 1000 matrix, with each column vector yk representing one iteration. This will allow HW6_6.m to make plots of what the iterations look like later. e) Calculate (and store in vectors Error and ErrorR) the L2-norms of both the proxy" error and the residual error for yk respectively. This will allow HW6_6.m to make a convergence history plot later. f) Create the variable Iter to be the final iteration number (k) once the solution yk finally converged (met both convergence criteria). When your GaussSeidel.m is complete, running HW6_6.m will automatically run your function and make two plots in one window. Save a.pdf of the plot window called Cable.pdf. Then study the plots and your calculated variables and answer the following questions: How many iterations did it take to converge? Hint: It took me around 20,000 iterations to converge, taking my code 5.5 seconds. Does the cable touch the hillside? Zoom in on the plot. If so, tell me at the lowest x value it first touches the hill. If not, tell me the minimum distance between the cable and the hill. (to the nearest 0.1 meters). iii. Which convergence criteria (proxy or residual) is achieved first? HINTS: 1. Sketch out on paper exactly what you need the remaining parts of your GaussSeidel.m function to do! Sketch what your final outputs should look like (the shapes of Yhistory, ErrorP and ErrorR matrices). Break the problem up into high-level jobs, then break that down into smaller parts, THEN start coding. Is your Gauss-Seidel iteration part working? (i.e. correctly getting Yk from the previous yk-1) You can double-check that part of your code alone against what you do know works. Take the 3x3 Ax=b problem we did in class using Gauss-Seidel iteration by-hand. We did the next iterations on the board. Your code should give exactly those results starting from those same A and b matrices. What about your while loop? We already went over this a lot in HW4.8. I don't fundamentally see anything different in how you would set it up here, except we're using norms of vectors to represent the errors, rather than just scalar errors before. Look at my solution to HW4.8 if you're not sure about this part. Any confusion about norms? Well, try them out separately in MATLAB, or by hand. Give it a smaller, known vector of errors as a test case and make sure you're using the norm command for L2-norms in MATLAB properly. Does your code just keep running without stopping? Then get more information WHY. Look at the one of the later iterations - is it getting closer to the final solution, or further away? Look at the "proxy" and residual errors - are they getting smaller, bigger, or kind-of staying the same? Most problems here are caused by (a) your iteration process is incorrect (see hint 2 above), (b) your while statement is not letting you end (see hint 3 above). HW6B HW6B (6.2 - 6.6) due FRIDAY February 21 6.6 6 pts Gauss-Seidel Iteration MATLAB code. OH NO!! I realized too late I didn't update this problem (your MATLAB problem for this week). Now I'm feeling really guilty, so I did much of the code for you, and I've instructed your TAs to give you more help than usual during Wednesday's recitation for the part that's left. Good luck! Let's extend exactly what we did for the hanging cable problem 6.1 with M = 6 points to M = 251 equally- spaced (Ax) points. So you'll set up a 251x251 system of equations, and then create your own Gauss- Seidel method to solve it in MATLAB. 10 Y Y2Y3 6 Assume the cable is the same as before: L = 10 meters, and boundary conditions Y = 6 and Y. = 10 meters. The difference now is that I have M = 251 unknown heights (Y, to Ym) as shown in the plot, so my Ax is much smaller, only L/(M-1) = 0.04 meter. Like HW6.1, I can approximate the differential equation with the linear relationship below: >AX AX hillside 1 y +1 = 0 0 2 2 10 4 6 (Ar) 2 8 (A Ar 10 x=L x=0 Substituting Ax = 0.04, this equation reduces to just: 628.125 Y_, -1250.1 Y, +621.875 Y = 0 If you don't understand where all this comes from, don't worry! You're going to be deriving this yourself by Chapter 10. For now, just accept the boxed equation applies for any three adjacent Y:-1, Y, Yi+1 (2 sis M-1). So, including the two boundary conditions (Y = Y, and YM = YR), you now can write 251 equations for all 251 unknown Y. In fact, the matrix Ax = b form of these equations would look exactly like: 628.125 -1250.1 621.875 628.125 -1250.1 621.875 628.125 -1250.1 621.875 628.125 -1250.1 621.875 To solve this I have posted a script HW6_6.m that already does all the following for you: Initializes variables for the cable (L, YU, YR), and M = 251, sets values for convergence tolerances for the L, norm of "proxy" error between iterations and the residual error (tolx = tolr = sqrt(M) x 10-3, using M = 251), calls a (incomplete!) function GaussSeidel.m to iteratively solve for all 251 Y, until convergence, Uses the results from GaussSeidel.m to make two plots: (i) the Y/(x) distribution for the 1st, 100th, 1000th, 5000th and final (converged) iterations compared to the exact solution, and (ii) the logo(error) convergence history. Your job is just to complete the function GaussSeidel.m that's called by the above code. HW6B HW6B (6.2 6.6) due FRIDAY February 21 6.6 Continued ... To help, I've actually already started your function for you. Upload the "code fragment" GaussSeidel.m in this same Carmen assignment. You'll see that I have: Given the 1st line of the function, to ensure compatibility with HW6_6.m. DON'T CHANGE IT!! function (Yhistory, ErrorP, ErrorR, Iter]= Gauss Seidel (L, YL, YR, M, tolx, tolR) Created the the A and b matrices from the last page, to make sure everyone's starting with the correct set of equations. Created the initial guess, Y, as the average value between the poles (Y +YR) = 8 m for all y. (I realize we called the first guess k=0 in class, but it's just a lot easier in this code to call it k=1.) Initialized the Yhistory, ErrorP and ErrorR matrices given that first k=1 guess: I just put the initial guess Y1 as the first column vector in Yhistory. Since we can't calculate a "proxy" error for the first guess (there is no previous iteration to compare it to), I just set the first value of "proxy" error vector Error P to be NaN (not a number"). That way it won't appear on the error plot later. We can calculate a residual error for the first guess, using the Lz-norm of AY -b, so I used that to start the residual error vector ErrorR. Your job is to now complete the function GaussSeidel.m to do the following: a) EXACTLY interfaces with my main script, using all the same inputs and outputs from the 1st line above. b) Calculate the column vector yk for each iteration k> 1 using the Gauss Seidel iterative method. c) Use a "while loop to keep iterating until the Lz-norms of both the "proxy" error between iterations and the residual error are within their tolerances. d) Store each iteration yk as a column vector in the variable Yhistory. So, for example, if you're done after k = 1000 iterations, then Yhistory would be a 251 x 1000 matrix, with each column vector yk representing one iteration. This will allow HW6_6.m to make plots of what the iterations look like later. e) Calculate (and store in vectors Error and ErrorR) the L2-norms of both the proxy" error and the residual error for yk respectively. This will allow HW6_6.m to make a convergence history plot later. f) Create the variable Iter to be the final iteration number (k) once the solution yk finally converged (met both convergence criteria). When your GaussSeidel.m is complete, running HW6_6.m will automatically run your function and make two plots in one window. Save a.pdf of the plot window called Cable.pdf. Then study the plots and your calculated variables and answer the following questions: How many iterations did it take to converge? Hint: It took me around 20,000 iterations to converge, taking my code 5.5 seconds. Does the cable touch the hillside? Zoom in on the plot. If so, tell me at the lowest x value it first touches the hill. If not, tell me the minimum distance between the cable and the hill. (to the nearest 0.1 meters). iii. Which convergence criteria (proxy or residual) is achieved first? HINTS: 1. Sketch out on paper exactly what you need the remaining parts of your GaussSeidel.m function to do! Sketch what your final outputs should look like (the shapes of Yhistory, ErrorP and ErrorR matrices). Break the problem up into high-level jobs, then break that down into smaller parts, THEN start coding. Is your Gauss-Seidel iteration part working? (i.e. correctly getting Yk from the previous yk-1) You can double-check that part of your code alone against what you do know works. Take the 3x3 Ax=b problem we did in class using Gauss-Seidel iteration by-hand. We did the next iterations on the board. Your code should give exactly those results starting from those same A and b matrices. What about your while loop? We already went over this a lot in HW4.8. I don't fundamentally see anything different in how you would set it up here, except we're using norms of vectors to represent the errors, rather than just scalar errors before. Look at my solution to HW4.8 if you're not sure about this part. Any confusion about norms? Well, try them out separately in MATLAB, or by hand. Give it a smaller, known vector of errors as a test case and make sure you're using the norm command for L2-norms in MATLAB properly. Does your code just keep running without stopping? Then get more information WHY. Look at the one of the later iterations - is it getting closer to the final solution, or further away? Look at the "proxy" and residual errors - are they getting smaller, bigger, or kind-of staying the same? Most problems here are caused by (a) your iteration process is incorrect (see hint 2 above), (b) your while statement is not letting you end (see hint 3 above)
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


