
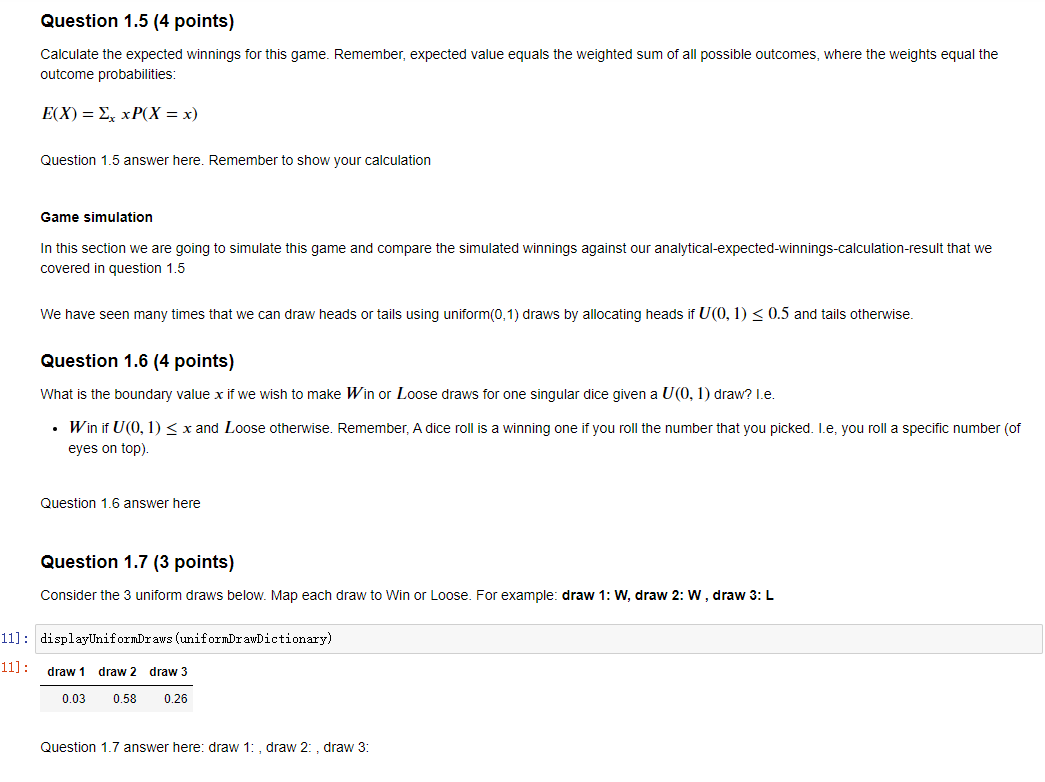
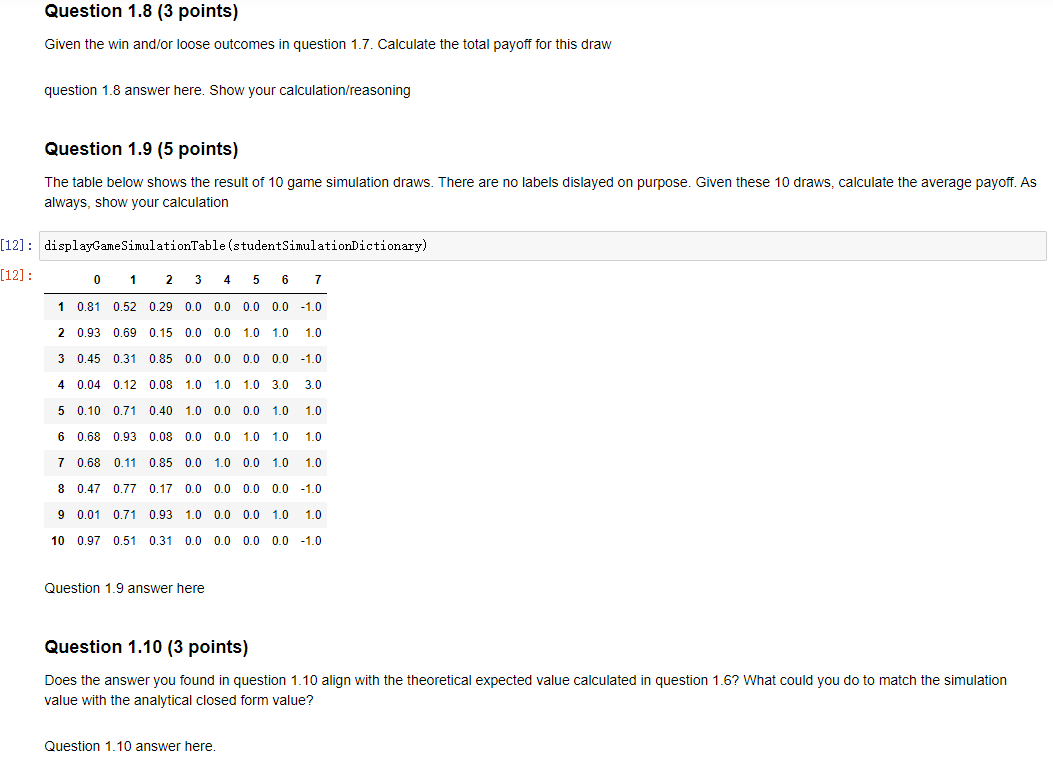
All, I need someone who is very good with statistics and probability to help on this...
In Lucky Deyes, players pick a number (1-6) and throw three dice. Money can be made or lost depending on the following outcomes (events): . If the number picked by the player does not appear at all: loose one dollar If the number picked by the player appears once: win one dollar . If the number picked by the player appears twice: win two dollars If the number picked by the player appears three times: win three dollars The game's payoff is summarized below 0] : generatePayoff Summary () 0] : Event Payoff Number does not appear Number appears once Number appears twice N Number appears three times Example Player chooses 4 and throws 2,4,6: Player wins 1 dollar, since the number 4 appears once Closed form analytical calculations ### Question 1.1 (2 points) You pick 4 and throw 3, 5, 3. What is your payoff? question 1.1 answer here This game can be modeled with a binomial model (just like heads and tails) with the probability of throwing a winning dice equal to 1/6 (throwing a specific number of eyes, the number that you poicked) and the probability to throw a loosing dice equal to 5/6 (not throwing a specific number of eyes). So in essence it is very similar to heads and tails: . H,T : P(H) = P(T) = 1/2 . W. L : P(W) = 1/6, P(L) = 5/6 W- >Win, L- >Loose, P(W): probability to throw one winning dice P(L): probability to throw one loosing diceQuestion 1.2 (2 points) Complete the sample space below with possible game outcomes S = {WWW, WLL, LWL, ... .., LLL} Question 1.2 answer here Question 1.3 (4 points) . a) How many permutations in the sample space represent 3 loosing dice (3 dice not equal to the number you picked)? . b) How many permutations in the sample space represent 2 loosing dice and 1 winning dice (2 dice not equal to the number you picked, 1 dice equal to the number you picked)? . c) How many permutations in the sample space represent 1 loosing dice and 2 winning dice (1 dice not equal to the number you picked, 2 dice equal to the number you picked)? . d) How many permutations in the sample space represent 3 winning dice (3 dice equal to the number you picked)? Question 1.3 answer here a) Question 1.4 (5 points) Given your answer to question 1.3 and the binomial probability formula: (") p(W)* p(L)"- . a) What is the probability to throw 3 loosing dice (3 dice not equal to the number you picked)? b) What is the probability to throw 2 loosing dice and 1 winning dice (2 dice not equal to the number you picked, 1 dice equal to the number you picked)? c) What is the probability to throw 1 loosing dice and 2 winning dice (1 dice not equal to the number you picked, 2 dice equal to the number you picked)? d) What is the probability to throw 3 winning dice (3 dice equal to the number you picked)? e) Verify that all these probabilities sum to 100%Question 1.5 (4 points) Calculate the expected winnings for this game. Remember, expected value equals the weighted sum of all possible outcomes, where the weights equal the outcome probabilities: E(X) = Ex xP(X = x) Question 1.5 answer here. Remember to show your calculation Game simulation In this section we are going to simulate this game and compare the simulated winnings against our analytical-expected-winnings-calculation-result that we covered in question 1.5 We have seen many times that we can draw heads or tails using uniform(0, 1) draws by allocating heads if U(0, 1)













