All of the figures below are related mathematically because the equations used to describe each figure are similar. The general form of the equation for each is Ax2 + Bxy + Cy2 + Dx + Ey + F = 0. They differ because of the restrictions placed on the coefficients in the table above. For the circle A and C must be equal and B must equal 0. For the ellipse, A and C cannot be equal but must have the same sign. B must equal 0. An example of an equation of a circle is: x2 + y2 + 4x - 6y 3 = 0. An example of an equation of an ellipse is: x2 + 4y2 - 6x - 16y 11 = 0. Write a Java program given the general form of the equation and determine if it is a circle, an ellipse, a hyperbola or a parabola and give other information about the figure.

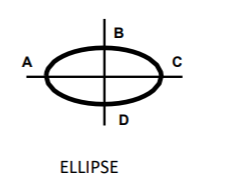
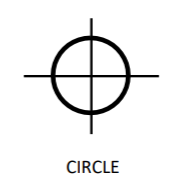
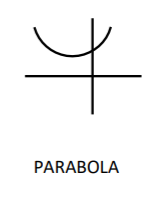
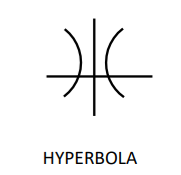
The general equation above is not very useful for determining information about the position of the figure on the coordinate axis system. The equation must be modified. The method commonly used is called "completing the square ". Using the equation of the circle above, the result is as follows:

x2 + 4x + 4 + y2 - 6y + 9 = 3 + 4 + 9

x2 + 4x + 4 + y2 - 6y + 9 = 16

(x + 2)2 + (y - 3)2 = 16 In this form, it is easy to find the center of the circle and its radius. The center is at (-2, 3) and the radius is 4 (the principal square root of 16).

Finding information about the ellipse is done in a similar manner. However, since the "completing the square" method only works when the coefficient of the squared term is a positive one, the second trinomial must be modified.

x2 + 4y2 - 6x - 16y 11 = 0

x2 - 6x + 9 + 4 (y2 - 4y + 4) = 11+ 9 + 16

(x 3)2 + 4(y - 2)2 = 36

In this form, the center of the ellipse can be found to be at (3, 2). If both sides of the equation are divided by the value on the right side, the equation is now said to be in standard form:

(x 3)2 / 36 + (y - 2)2 / 9 = 1

In the figure of the ellipse, above, line segments AC and BD are axes. Since segment AC is longer it is called the major axis and since BD is shorter it is called the minor axis. The bigger denominator above determines the major axis. Its length is found by taking two times the principal square root of the denominator. Here the major axis will have a length of 12 and in a similar manner, the minor axis will have a length of 6.

Using the procedures above, examples of equations of a hyperbola in standard form are as follows:

(x 3)2 / 1 - (y - 2)2 / 3 = 1

(y - 2)2 / 1 - (x 3)2 / 3 = 1

The center of both hyperbolas is (3, 2). Since the general equation that produced the standard form on the left had a positive A and a negative C, the principal axis, the line that connects the foci and passes through the center, is the line y = 2. The standard form on the right had a negative A and a positive C and has a principal axis of x = 3.

Again, using the procedures above, examples of equations of a parabola in standard form are as follows:

(x - 3)2 = 12(y 1)

(y 1)2 = 12(x 3)

The vertex of both parabolas is (3, 1). Since the general form of the equation for the standard form on the left had C = 0, the axis of symmetry, is x = 3. The general form of the equation for the standard form on the right had A = 0 and its axis of symmetry is y = 1.

Input will be from a data file. The first value is the number of data sets in the file. Each set will contain six integers A, B, C, D, E and F that represent the coefficients of the general equation. For each set of data, print the type of figure the equation produces to the screen. If it is a circle, print the location of its center in ordered pair format (x,y) and its radius. If it is an ellipse, print the location of its center and the length of its major axis. If it is a hyperbola, print its center and the equation of the principal axis. If it is a parabola, print its vertex and the equation of the axis of symmetry. Let the user enter the file name from the keyboard.

Refer to the sample output below.

Sample Input File:

3

x^2+y^2+4x-6y-3=0

x^2+4y^2-6x-16y-11=0

2x^2+2y^2+8x+12y-6=0

Sample Run:

Enter the file name: conic.txt

Circle, (-2,3), 4

Ellipse, (3,2), 12

Circle, (-2,-3), 4

Name the program: ConicsXX.java, where XX are your initials

ELLIPSE