

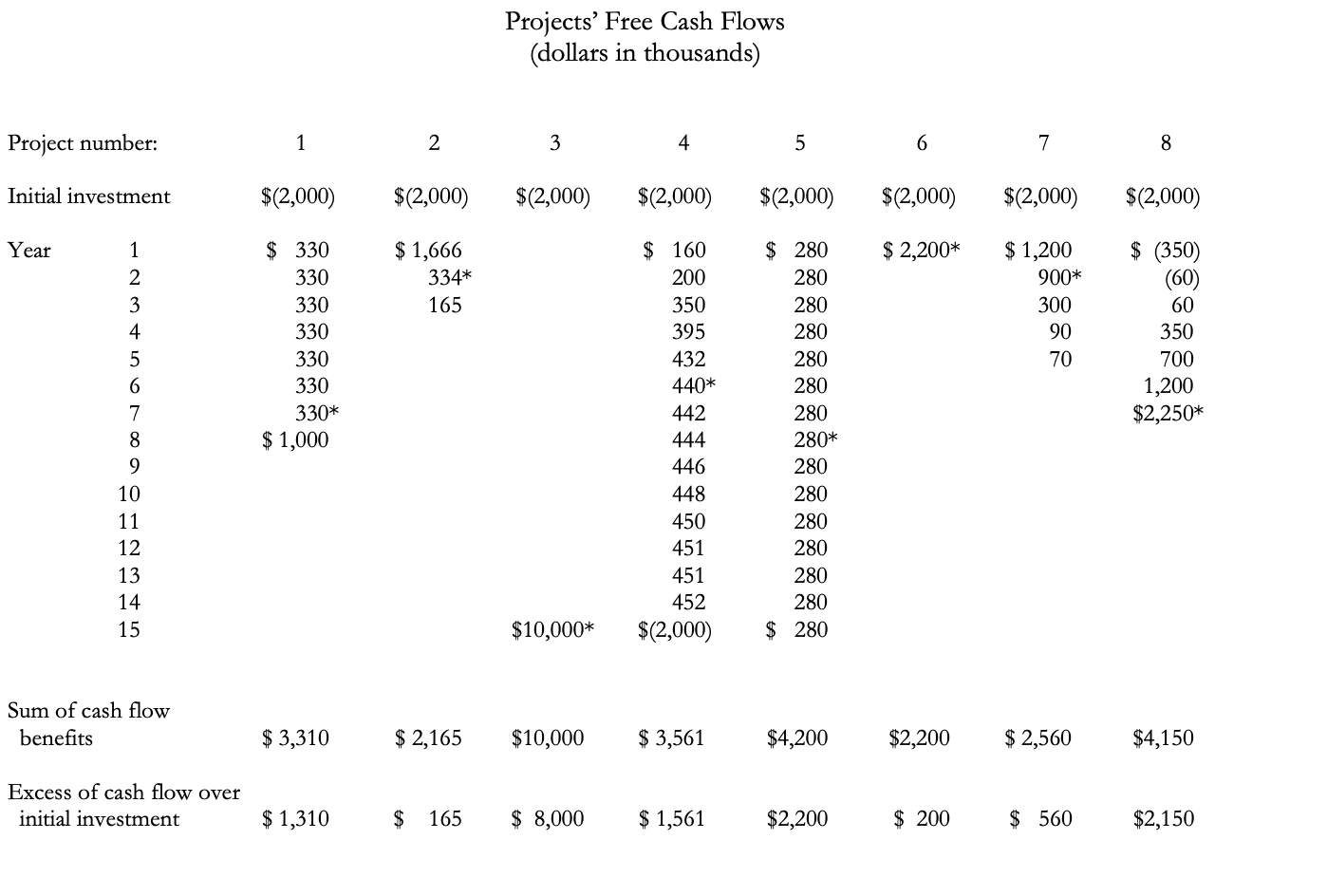

All the projects require the same initial investment, $2 million. Moreover, all are believed to be of the same risk class. The firm's weighted average cost of capital has never been estimated. In the past, analysts have simply assumed that 10% was an appropriate discount rate (although certain officers of the company have recently asserted that the discount rate should be much higher). To stimulate your analysis, consider the following questions: 1. Can you rank the projects simply by inspecting the cash flows? 2. What criteria might you use to rank the projects? Which quantitative ranking methods are better? Why? 3. What is the ranking you found by using quantitative methods? Does this ranking differ from the ranking obtained by simple inspection of the cash flows? 4. What kinds of real investment projects have cash flows similar to those in Exhibit 1? Do NOT answer the questions in the case. Instead, calculate the IRR and NPV of all 8 potential projects. Initial Investment is made in "Year O". Use a WACC of 10%. In capital budgeting, sometimes there is a terminal value and sometimes there is not. In the Investment Detective case, there is no terminal value, so you do not need to add a terminal value into the calculation. NOTE: In Excel, if you have $0 return in a given year, you should put a $0 in the cell; otherwise, Excel assumes if the cell is blank (i.e., no data is in the cell) and does not count it as a period of time. Therefore, if you do not earn any returns until a later year, you should put a 0 in the cells leading up to that later year. Projects' Free Cash Flows (dollars in thousands) Project number: 1 2 3 4 5 6 7 8 Initial investment $(2,000) $(2,000) $(2,000) $(2,000) $(2,000) $(2,000) $(2,000) $(2,000) Year 1 $ 2,200* $ 1,666 334* 165 $ 1,200 900* 300 $ 330 330 330 330 330 330 330* $ 1,000 90 70 $ (350) (60) 60 350 700 1,200 $2,250* 2 3 4 5 6 7 8 9 10 11 12 13 14 15 $ 160 200 350 395 432 440* 442 444 446 448 450 451 451 452 $(2,000) $ 280 280 280 280 280 280 280 280* 280 280 280 280 280 280 $ 280 $10,000* Sum of cash flow benefits $ 3,310 $ 2,165 $10,000 $ 3,561 $4,200 $2,200 $ 2,560 $4,150 Excess of cash flow over initial investment $ 1,310 $ 165 $ 8,000 $ 1,561 $2,200 $ 200 $ 560 $2,150 NPV for Project 2 (Input in Whole $ without the $ sign - for example $1,243.58 would be input as 1244; if negative be sure to enter "-" before the number) All the projects require the same initial investment, $2 million. Moreover, all are believed to be of the same risk class. The firm's weighted average cost of capital has never been estimated. In the past, analysts have simply assumed that 10% was an appropriate discount rate (although certain officers of the company have recently asserted that the discount rate should be much higher). To stimulate your analysis, consider the following questions: 1. Can you rank the projects simply by inspecting the cash flows? 2. What criteria might you use to rank the projects? Which quantitative ranking methods are better? Why? 3. What is the ranking you found by using quantitative methods? Does this ranking differ from the ranking obtained by simple inspection of the cash flows? 4. What kinds of real investment projects have cash flows similar to those in Exhibit 1? Do NOT answer the questions in the case. Instead, calculate the IRR and NPV of all 8 potential projects. Initial Investment is made in "Year O". Use a WACC of 10%. In capital budgeting, sometimes there is a terminal value and sometimes there is not. In the Investment Detective case, there is no terminal value, so you do not need to add a terminal value into the calculation. NOTE: In Excel, if you have $0 return in a given year, you should put a $0 in the cell; otherwise, Excel assumes if the cell is blank (i.e., no data is in the cell) and does not count it as a period of time. Therefore, if you do not earn any returns until a later year, you should put a 0 in the cells leading up to that later year. Projects' Free Cash Flows (dollars in thousands) Project number: 1 2 3 4 5 6 7 8 Initial investment $(2,000) $(2,000) $(2,000) $(2,000) $(2,000) $(2,000) $(2,000) $(2,000) Year 1 $ 2,200* $ 1,666 334* 165 $ 1,200 900* 300 $ 330 330 330 330 330 330 330* $ 1,000 90 70 $ (350) (60) 60 350 700 1,200 $2,250* 2 3 4 5 6 7 8 9 10 11 12 13 14 15 $ 160 200 350 395 432 440* 442 444 446 448 450 451 451 452 $(2,000) $ 280 280 280 280 280 280 280 280* 280 280 280 280 280 280 $ 280 $10,000* Sum of cash flow benefits $ 3,310 $ 2,165 $10,000 $ 3,561 $4,200 $2,200 $ 2,560 $4,150 Excess of cash flow over initial investment $ 1,310 $ 165 $ 8,000 $ 1,561 $2,200 $ 200 $ 560 $2,150 NPV for Project 2 (Input in Whole $ without the $ sign - for example $1,243.58 would be input as 1244; if negative be sure to enter "-" before the number)










