Although the constraint

x1 − x2 ≤ −1

and the constraint

 −x1 + 2x2 ≤ −1

 to a zero–one integer program both have feasible solutions, the system composed of both constraints is infeasible. One way to exhibit the inconsistency in the system is to add the two constraints, producing the constraint

x2 ≤ −1,

 which has no feasible solution with x2 = 0 or 1.

 More generally, suppose that we multiply the i_th constraint of a system

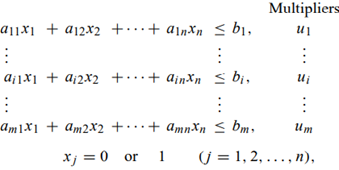
by nonnegative constraints ui and add to give the composite, or surrogate, constraint:

a) Show that any feasible solution xj = 0 or 1 (j = 1, 2, . . . , n) for the system of constraints must also be feasible to the surrogate constraint.

b) How might the fathoming tests discussed in the previous exercise be used in conjunction with surrogate constraints in an implicit enumeration scheme?

 c) A ‘‘best’’ surrogate constraint might be defined as one that eliminates as many nonoptimal solutions xj = 0 or 1 as possible. Consider the objective value of the integer program when the system constraints are replaced by the surrogate constraint; that is the problem:

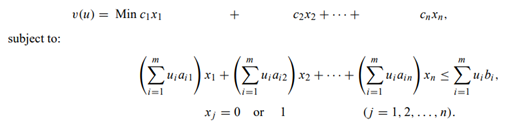
Let us say that a surrogate constraint with multipliers u1, u2 . . . , um is stronger than another surrogate constraint with multipliers u1, u2, . . . , um, if the value v(u) of the surrogate constraint problem with multipliers u1, u2, . . . , um is larger than the value of v(u) with multipliers u1, u2, . . . , um. (The larger we make v(u), the more nonoptimal solutions we might expect to eliminate.) Suppose that we estimate the value of v(u) defined above by replacing x j = 0 or 1 by 0 ≤ xj ≤ 1 for j = 1, 2, . . . , n. Then, to estimate the strongest surrogate constraint, we would need to find those values of the multipliers u1, u2, . . . , um to maximize v(u), where

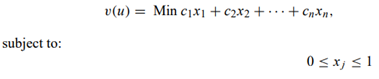
and the surrogate constraint. Show that the optimal shadow prices to the linear program

solve the problem of maximizing v(u) in (1).

a11x +a12x2 +...+anxn b, a1x + a2x2 + + ainxn bi, amix1 + am2x2 + ... + amnxn bm, xj = 0 or 1 Multipliers UI : Ui : Um (j= 1, 2, ...,n),