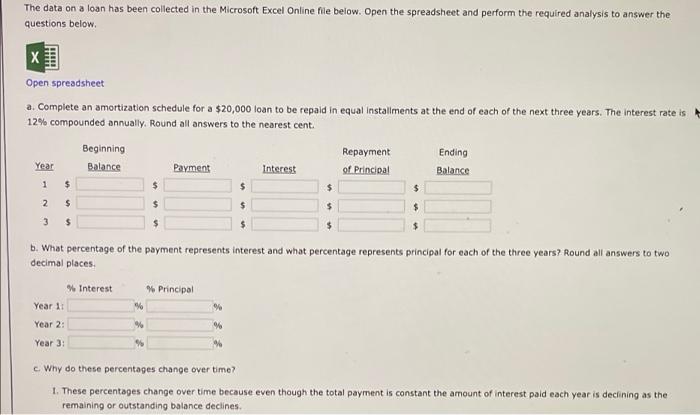
amount to be repaid (PV) ist rate (r) h of loan (in years) tting up amortization table lation of loan payment Year Beginning Balance 1 2 3 alculating % of Payment Representing Interest and Payment % Payment % Representing Interest Year Representing Principal 1 ulas Year Beginning Balance Payment #N/A 1 #N/A 2 #N/A #N/A 3 #N/A #N/A alculating % of Payment Representing Interest and Principal for Each Year Payment % Payment % Representing Interest. Year Representing Principal #N/A 1 #N/A 2 #N/A #N/A 3 #N/A #N/A 23 $20,000.00 12.00% 3 Formula #N/A Payment for Each Year Y 2 Interest Check: Total = 100% Interest #N/A #N/A #N/A Check: Total= 100% #N/A #N/A #N/A Y E Repayment of Principal Repayment of Principal #N/A #N/A #N/A F Remaining Balance Remaining Balance #N/A #N/A #N/A The data on a loan has been collected in the Microsoft Excel Online file below. Open the spreadsheet and perform the required analysis to answer the questions below. X Open spreadsheet a. Complete an amortization schedule for a $20,000 loan to be repaid in equal installments at the end of each of the next three years. The interest rate is 12% compounded annually. Round all answers to the nearest cent. Beginning Repayment of Principal Ending Balance Year Balance Payment Interest 1 $ $ $ 2 $ $ $ $ $ 3 $ $ $ $ $ b. What percentage of the payment represents interest and what percentage represents principal for each of the three years? Round all answers to two decimal places. % Interest % Principal Year 1: % Year 2: % Year 3: % c. Why do these percentages change over time? 1. These percentages change over time because even though the total payment is constant the amount of interest paid each year is declining as the remaining or outstanding balance declines. $ $ c. Why do these percentages change over time? 1. These percentages change over time because even though the total payment is constant the amount of interest paid each year is declining as the remaining or outstanding balance declines. II. These percentages change over time because even though the total payment is constant the amount of interest paid each year is increasing as the remaining or outstanding balance declines. III. These percentages change over time because even though the total payment is constant the amount of interest paid each year is declining as the remaining or outstanding balance increases. IV. These percentages change over time because even though the total payment is constant the amount of interest paid each year is increasing as the remaining or outstanding balance increases. V. These percentages do not change over time; interest and principal are each a constant percentage of the total payment