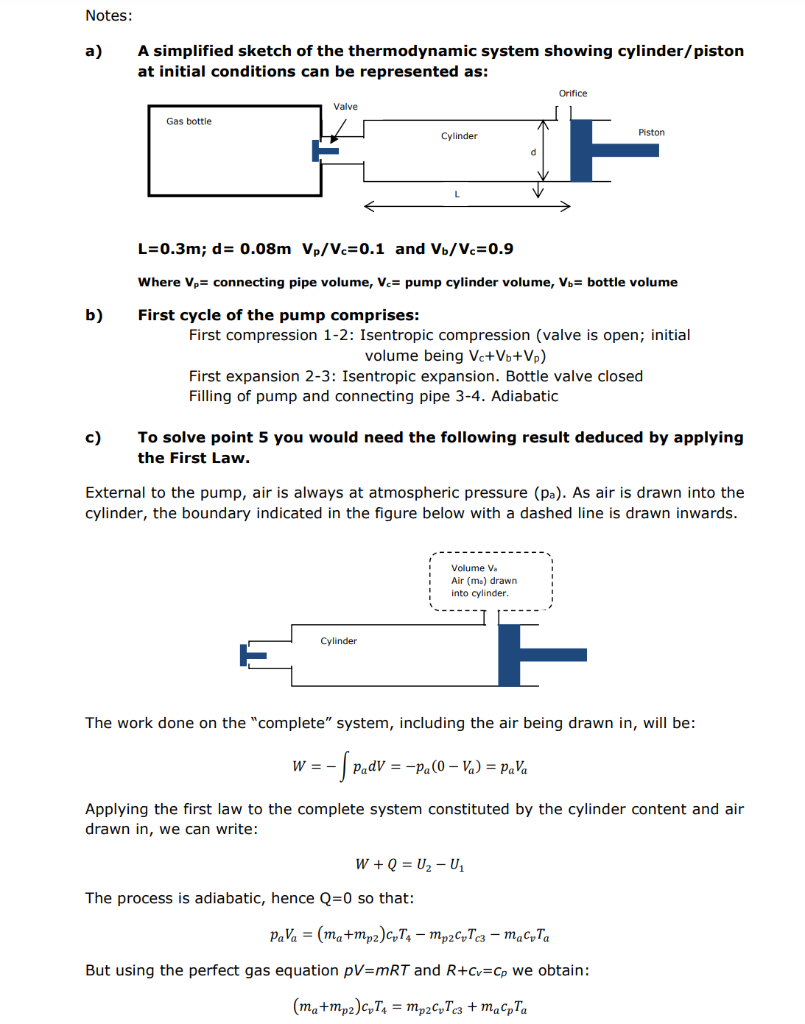
An air pump is used to fill a rigid gas bottle with air. The pump is connected to the gas bottle via a rigid pipe. The pump consists of a piston of internal diameter d=0.08m and a cylinder with a stroke L=0.3m. Air enters the pump through an orifice located at the bottom of the cylinder to raise the pressure in the pump to atmospheric pressure. Air, drawn into the pump through the orifice, mixes completely and adiabatically with the cylinder contents. A valve allows the bottle's refill. The valve opens when the pump pressure is equal to the gas bottle. The valve is always closed when the pump pressure is below the gas bottle pressure. Pressure drop across the valve can be neglected. The bottle, the connecting pipe and the pump are thermally insulated. Air in the pump and connecting pipe undergoes isentropic compression and expansion processes. The working fluid (air) can be considered a perfect gas with R=287J/KgK,cp=1005J/KgK and =1.4. Initially the piston is located at the bottom of the cylinder, the valve is open and pressure and temperature are 1 bar and 298K in the pump, the bottle and the surrounding ambient air. Air transferring to the gas bottle mixes completely and adiabatically on entering. See notes on page two for more information and power point presentation on Moodle. Determine: 1) The initial masses of air in the bottle (mb), cylinder (mc) and connecting pipe (mp). 2) The mass in the bottle (mb2), in the connecting pipe (mp2) and the mass that has been transferred to the bottle after the first compression stroke. 3) Calculate the pressure and temperature of the air in the bottle after the first compression stroke. a) A simplified sketch of the thermodynamic system showing cylinder/piston at initial conditions can be represented as: L=0.3m;d=0.08mVp/Vc=0.1 and Vb/Vc=0.9 Where vp= connecting pipe volume, vc= pump cylinder volume, vb= bottle volume b) First cycle of the pump comprises: First compression 1-2: Isentropic compression (valve is open; initial volume being Vc+Vb+Vp ) First expansion 2-3: Isentropic expansion. Bottle valve closed Filling of pump and connecting pipe 3-4. Adiabatic c) To solve point 5 you would need the following result deduced by applying the First Law. External to the pump, air is always at atmospheric pressure (pa). As air is drawn into the cylinder, the boundary indicated in the figure below with a dashed line is drawn inwards. The work done on the "complete" system, including the air being drawn in, will be: W=padV=pa(0Va)=paVa Applying the first law to the complete system constituted by the cylinder content and air drawn in, we can write: W+Q=U2U1 The process is adiabatic, hence Q=0 so that: paVa=(ma+mp2)cvT4mp2cvTc3macvTa But using the perfect gas equation pV=mRT and R+cv=cp we obtain: (ma+mp2)cvT4=mp2cvTc3+macpTa