Question
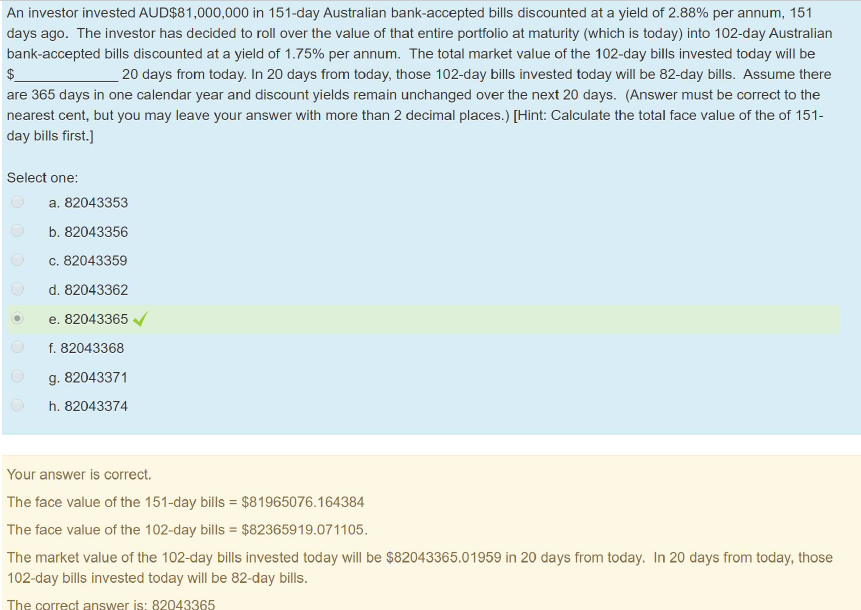
An investor invested AUD$89,000,000 in 163-day Australian bank-accepted bills discounted at a yield of 2.17% per annum, 163 days ago. The investor has decided to
An investor invested AUD$89,000,000 in 163-day Australian bank-accepted bills discounted at a yield of 2.17% per annum, 163 days ago. The investor has decided to roll over the value of that entire portfolio at maturity (which is today) into 109-day Australian bank-accepted bills discounted at a yield of 1.94% per annum. The total market value of the 109-day bills invested today will be $_____________ 20 days from today. In 20 days from today, those 109-day bills invested today will be 89-day bills. Assume there are 365 days in one calendar year and discount yields remain unchanged over the next 20 days. (Answer must be correct to the nearest cent, but you may leave your answer with more than 2 decimal places.) [Hint: Calculate the total face value of the of 163-day bills first.]
Select one: a. 89957537 b. 89957540 c. 89957543 d. 89957546 e. 89957549 f. 89957552 g. 89957555 h. 89957558
I got a same question with answer, but the number is different. But I really don't know the process of the calculation. plz provide the answer of the above question n the process. Thx
Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


