An irregular example of n1 = 10 districts in New England gave the accompanying savage crime percentages (per million populace).

x1: New England Crime Rate

3.5 3.9 4.0 4.1 3.3 4.1 1.8 4.8 2.9 3.1

Another irregular example of n2 = 12 districts in the Rocky Mountain states gave the accompanying brutal crime percentages (per million populace).

x2: Rocky Mountain Crime Rate

3.7 4.1 4.7 5.1 3.3 4.8 3.5 2.4 3.1 3.5 5.2 2.8

(a) Assume that the crime percentage appropriation is around typical in the two locales. Utilize a mini-computer to ascertain x1, s1, x2, and s2. (Round your responses to two decimal spots.)

x1 =

s1 =

x2 =

s2 =

(b) What is the estimation of the example test measurement? Process the comparing z or t esteem as proper. (Test the distinction ?1 ? ?2. Try not to utilize adjusted qualities. Round your response to three decimal spots.)

(c) Find a 98% certainty span for ?1 ? ?2. (Round your responses to two decimal spots.)

lower limit

furthest breaking point

PC console disappointments can be ascribed to electrical imperfections or mechanical deformities. A maintenance office at present has 25 bombed consoles, 11 of which have electrical deformities and 14 of which have mechanical imperfections.

On the off chance that an example of 6 consoles is haphazardly chosen, what is the likelihood that in any event 5 of these will have a mechanical deformity?

Assume we notice 84 drunkards with cirrhosis of the liver, of whom 29 have hepatomas?that is, liver-cell carcinoma.

@30@

Assume we know, in view of a huge example, that the danger of hepatoma among drunkards without cirrhosis of the liver is 24%.

1-What is the likelihood that we notice precisely 29 drunkards with cirrhosis of the liver who have hepatomas if the genuine pace of hepatoma among heavy drinkers (with or without cirrhosis of the liver) is .24?

2-What is the likelihood of seeing at any rate 29 hepatomas among the 84 heavy drinkers with cirrhosis of the liver under the suppositions in Problem 5.50?

3-What is the most modest number of hepatomas that would need to be seen among the drunkards with cirrhosis of the liver for the hepatoma experience in this gathering to contrast from the hepatoma experience among heavy drinkers without cirrhosis of the liver? (Clue: Use a 5% likelihood of getting an outcome in any event as outrageous to indicate contrasts between the hepatoma encounters of the two gatherings.)

l need the arrangement as a Rstudio program

Hypertension

A public report found that treating individuals properly for

hypertension decreased their general mortality by 20%.

Treating individuals sufficiently for hypertension has been troublesome in light of the fact that it is assessed that half of hypertensives do

not realize they have hypertension, half of the individuals who

do know are insufficiently treated by their doctors, and

half who are suitably treated neglect to follow this treatment by taking the correct number of pills.

4.32 If the first half rates were each decreased to

40% by monstrous schooling program, at that point what impact

would this change have on the general death rate among

genuine hypertensives; that is, would the death rate decline

furthermore, assuming this is the case, which level of passings among hypertensives

could be forestalled by the training program?

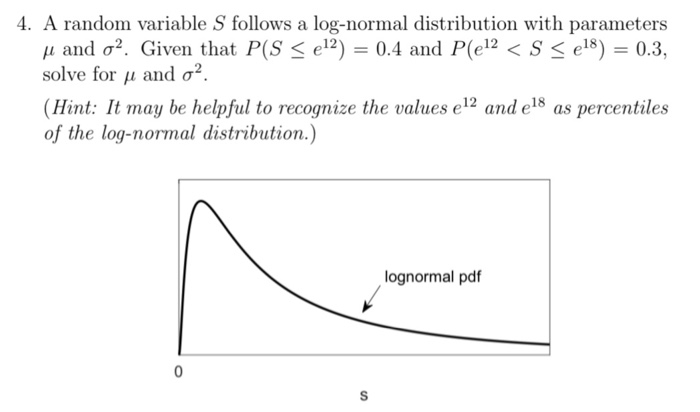
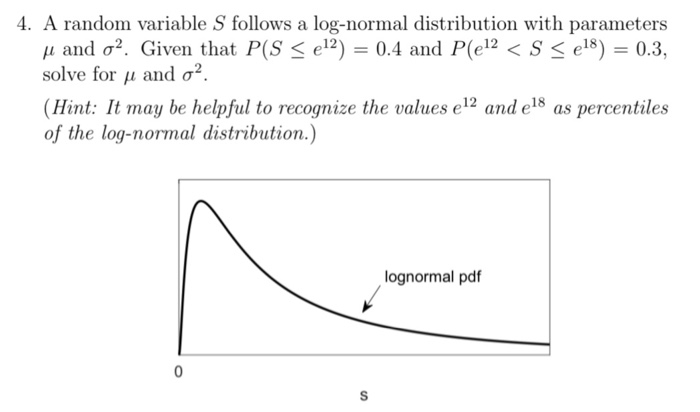
4. An inequality developed by Russian mathematician Chebyshev gives the minimum percentage of values in ANY sample that can be found within some number ( 1) standard deviations from the mean. Let P be the percentage of values within k standard deviations of the mean value. Chebyshevs inequality states that for ANY distribution, P 100 * (1 -1/k)2. (a) For any distribution, what does Chebyshevs inequality say about the percentage of values that are within 2, 3, 5, 10 standard deviations of the mean? (b) For each of the distributions below, determine the percentage of observations within 2 and 3 standard deviations of the mean value. Comment on how these percentages compare to the percentage found using Chebyshevs inequality. i. A standard normal distribution (X ~ N(0,1)) ii. An exponential distribution with A = 2 (X ~ exp(2)) iii. A Poisson distribution with A = 2 X ~Pois(2) iv. A binomial distribution with n = 10 and p = 0.2. X ~ binom(10,0.45)2.4 Chebyshev inequality (20 points) Let X be a random variable such that E[X] = 0. It is estimated from experi- ments that P(|X | 2 1) 2 7. a) What can you say about its variance using Chebyshev inequality? b) Now assume that X is uniformly distributed on the interval [-a, a]. What can you say about its variance?4. A random variable S follows a log-normal distribution with parameters u and o'. Given that P(S