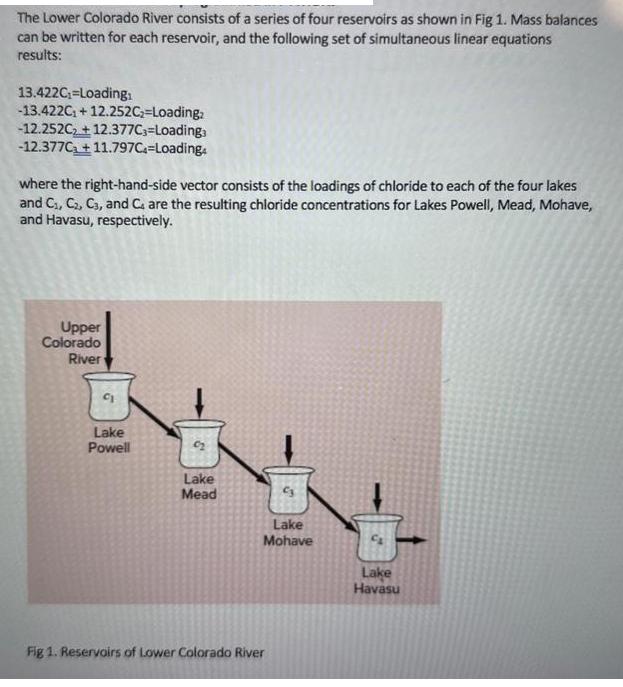
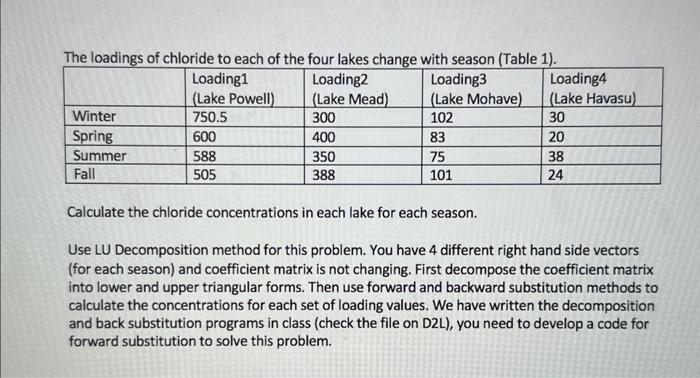
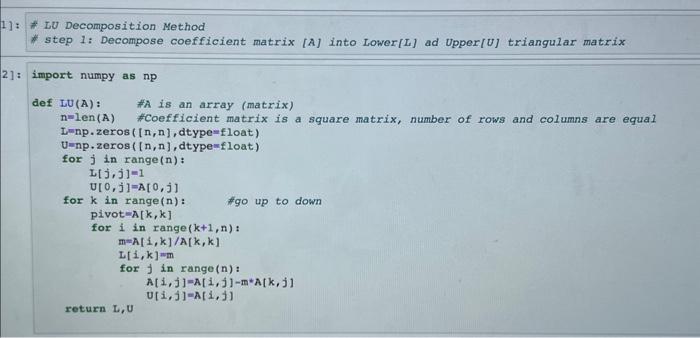
The Lower Colorado River consists of a series of four reservoirs as shown in Fig 1. Mass balances can be written for each reservoir, and the following set of simultaneous linear equations results: 13.422C-Loading: -13.422C+12.252C-Loading: -12.252C+12.377C3=Loading -12.377C+11.797C-Loading where the right-hand-side vector consists of the loadings of chloride to each of the four lakes and C, C2, C3, and C are the resulting chloride concentrations for Lakes Powell, Mead, Mohave, and Havasu, respectively. Upper Colorado River 9 Lake Powell Lake Mead Lake Mohave Lake Havasu Fig 1. Reservoirs of Lower Colorado River The loadings of chloride to each of the four lakes change with season (Table 1). Loading1 (Lake Powell) Loading2 (Lake Mead) Loading3 (Lake Mohave) Loading4 (Lake Havasu) Winter 750.5 300 102 30 Spring 600 400 83 20 Summer 588 350 75 38 Fall 505 388 101 24 Calculate the chloride concentrations in each lake for each season. Use LU Decomposition method for this problem. You have 4 different right hand side vectors (for each season) and coefficient matrix is not changing. First decompose the coefficient matrix into lower and upper triangular forms. Then use forward and backward substitution methods to calculate the concentrations for each set of loading values. We have written the decomposition and back substitution programs in class (check the file on D2L), you need to develop a code for forward substitution to solve this problem. 1]: def Back_sub (U,Y): n=len (Y) #U is upper triangular matrix and #Y is the result of foward substitution #number of unknowns X=np.zeros([n, 1]) x[n-1,0]=Y[n-1,0]/U[n-1, n-1] for i in range (n-2,-1,-1): sum=0 for j in range (i+1,n): return X sum sum+U[i, j]*X[j,0] X[1,0]=(Y[1,0]-sum)/U[i,i] 11: #LU Decomposition Method #step 1: Decompose coefficient matrix [A] into Lower [L] ad Upper[U] triangular matrix 21: import numpy as np def LU(A): # A is an array (matrix) n-len (A) #Coefficient matrix is a square matrix, number of rows and columns are equal L-np.zeros([n,n], dtype-float) U-np.zeros([n,n], dtype-float) for j in range(n): L[3,3]-1 U[0,1]-A[0,1] for k in range(n): pivot-A[k, k] #go up to down for i in range(k+1,n): m-Ali, k]/A[k, k] L[i,k]-m for in range(n): A[i, j] A[i, j]-m*A[k, j] U[i, j]-A[i, j] return L, U