Answered step by step
Verified Expert Solution
Question
1 Approved Answer
an overall score of 94.8 , the highest component of which is 100.0 for amenities. If required, round your answers to three decimal places. Click
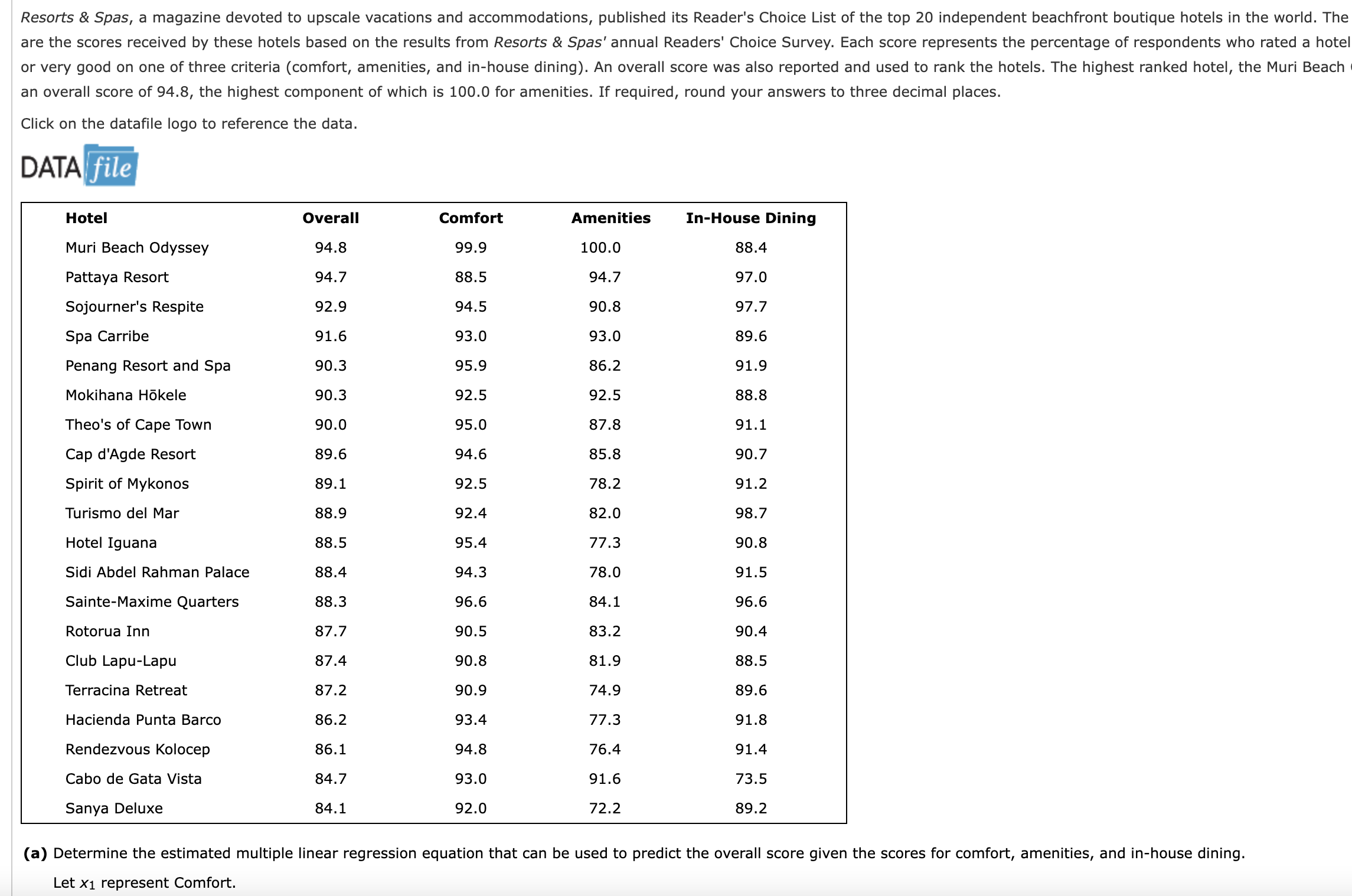

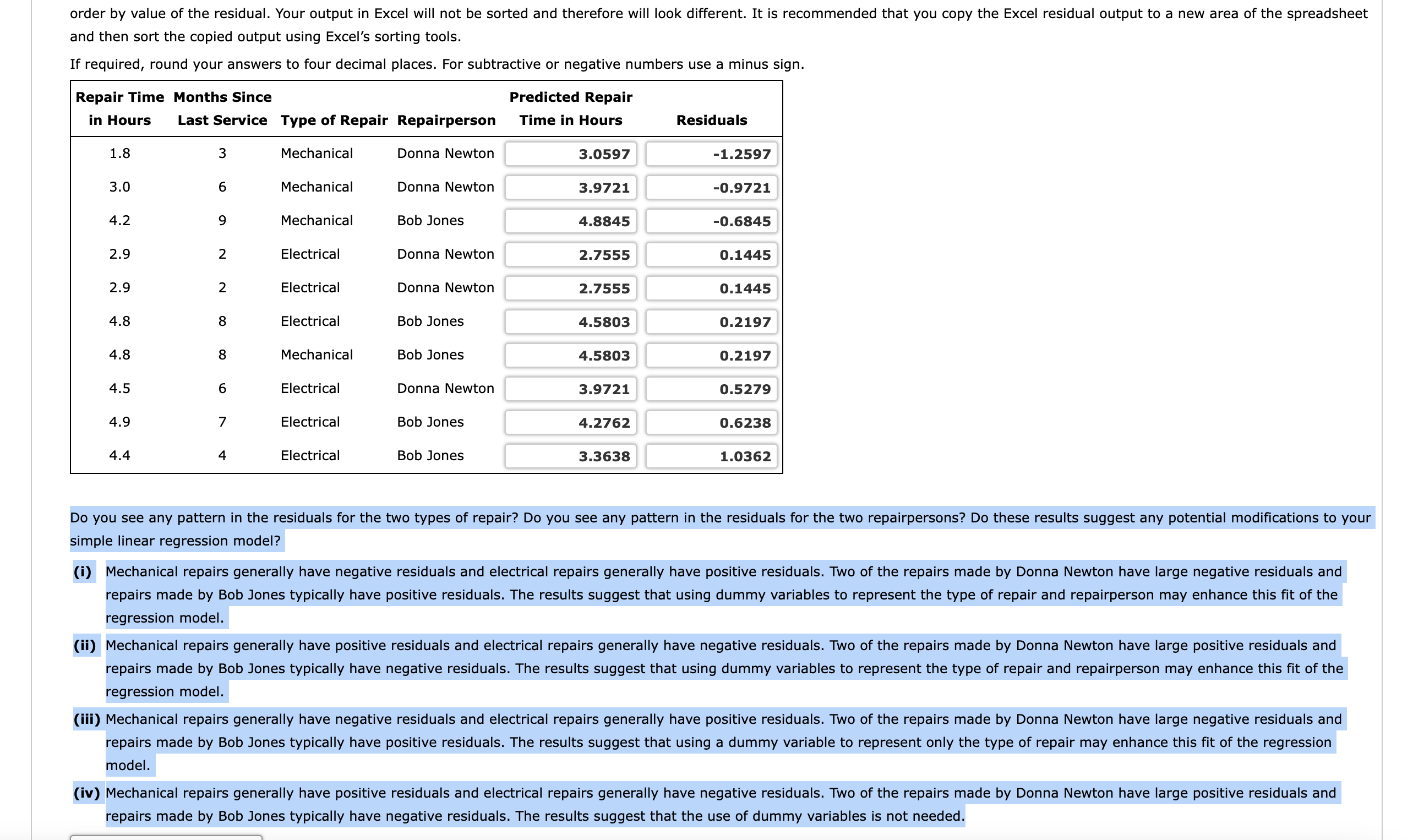
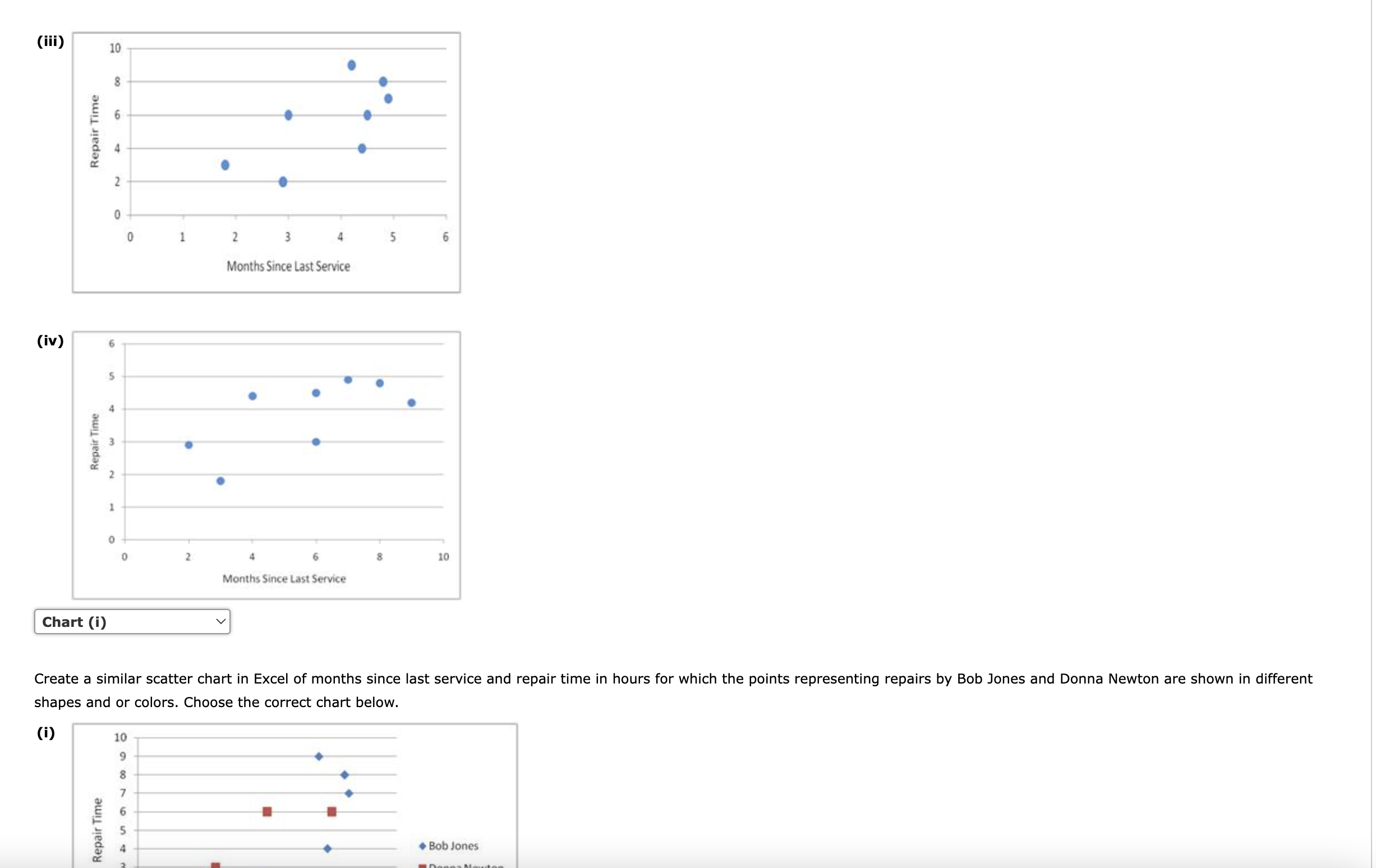

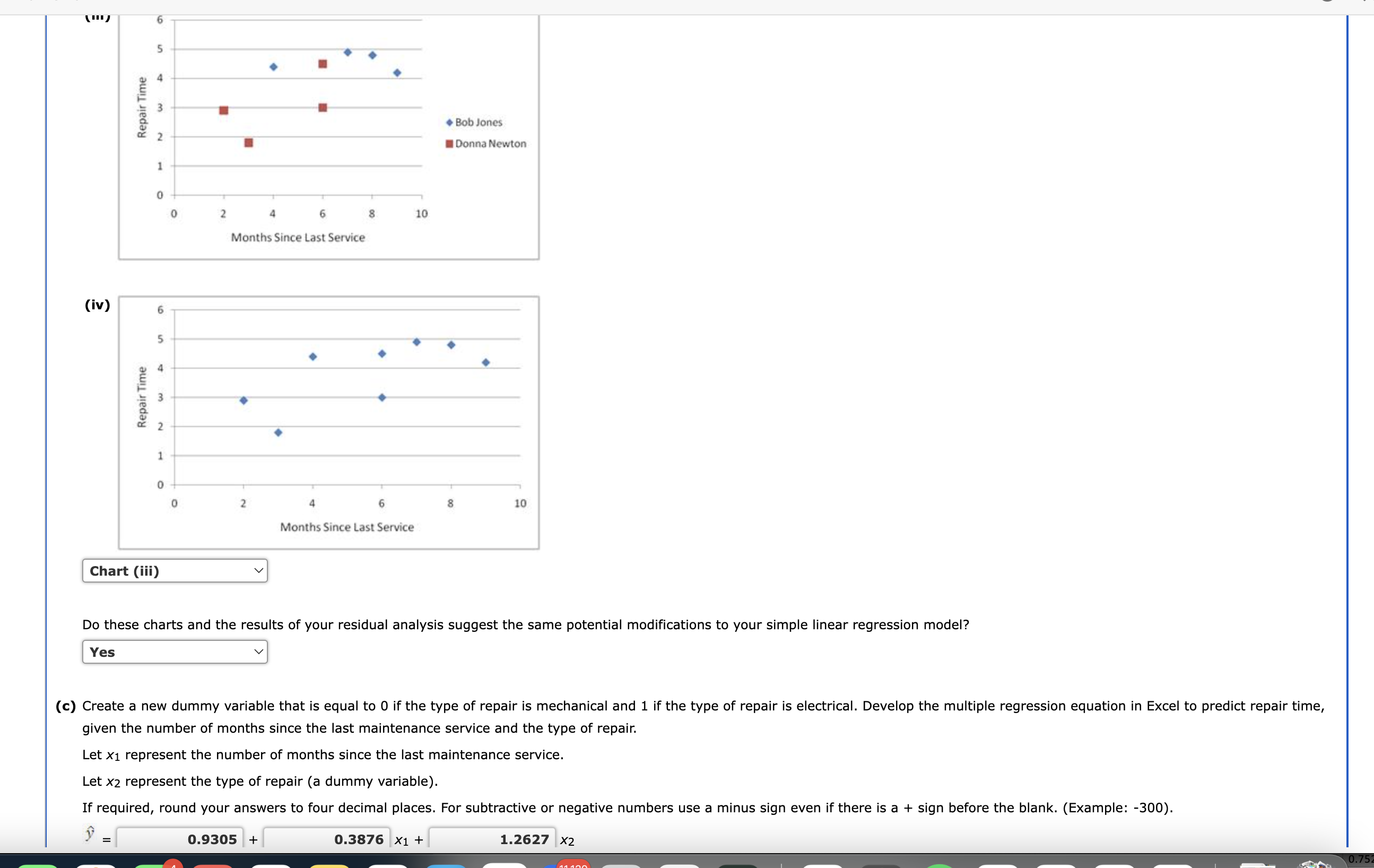



 an overall score of 94.8 , the highest component of which is 100.0 for amenities. If required, round your answers to three decimal places. Click on the datafile logo to reference the data. DATA Let x1 represent Comfort. and then sort the copied output using Excel's sorting tools. If required, round your answers to four decimal places. For subtractive or negative numbers use a minus sign. simple linear regression model? regression model. regression model. model. repairs made by Bob Jones typically have negative residuals. The results suggest that the use of dummy variables is not needed. of repair constant and the repairperson is Bob Jones. What is the coefficient of determination? If required, round your answers to four decimal places. Interpret the coefficient of determination. If required, round your answer to one decimal place. This regression model explains approximately % of the variation in the values of repair time in the sample. (f) Which of these models would you use? Why? (i) The preferred model is the one with the lowest coefficient of determination, so the best model to use is in part (c). (ii) The preferred model is the one with the lowest coefficient of determination, so the best model to use is in part (d). (iii) The preferred model is the simplest that works well, so the best model to use is in part (c). (iv) The preferred model is the one with the highest coefficient of determination, so the best model to use is in part (c). (v) The preferred model is the one with the highest coefficient of determination, so the best model to use is in part (d). time, given the number of months since the last maintenance service and the repairperson. Let x1 represent the number of months since the last maintenance service. Let x2 represent the repairperson (a dummy variable). y^=+x1+x2 What are the interpretations of the estimated regression parameters? What is the coefficient of determination? If required, round your answers to four decimal places. Interpret the coefficient of determination. If required, round your answer to one decimal place. This regression model explains approximately % of the variation in the values of repair time in the sample. Let x1 represent the number of months since the last maintenance service. Let x2 represent the type of repair (a dummy variable). Let x3 represent the repairperson (a dummy variable). Let x1 represent the number of months since the last maintenance service. Let x2 represent the type of repair (a dummy variable). Let x3 represent the repairperson (a dummy variable). y^=+x1+x2+x3 What are the interpretations of the estimated regression parameters? mechanical. is Donna Newton. of repair constant and the repairperson is Bob Jones. What is the coefficient of determination? If required, round your answers to four decimal places. Interpret the coefficient of determination. If required, round your answer to one decimal place. This regression model explains approximately % of the variation in the values of repair time in the sample. Which of these models would you use? Why? (i) The preferred model is the one with the lowest coefficient of determination, so the best model to use is in part (c). Create a similar scatter chart in Excel of months since last service and repair time in hours for which the points representing repairs by Bob Jones and Donna Newton are shown in different shapes and or colors. Choose the correct chart below. (a) Determine the estimated multiple linear regression equation that can be used to predict the overall score given the scores for comfort, amenities, and in-house dining. Let x1 represent Comfort. Let x2 represent Amenities. Let x3 represent In-House Dining. y^=+x1+x2+x3 The p-value associated with the estimated regression parameter b1 is the hypothesis that 1=0. We conclude that there of significance when controlling for The p-value associated with the estimated regression parameter b2 is the hypothesis that 2=0. We conclude that there of significance when controlling for The p-value associated with the estimated regression parameter b3 is the hypothesis that 3=0. We conclude that there Because this p-value is Because this p-value is . Because this p-value is Because this p-value is ( 0.01 level of significance when controlling for than the level of significance, we a relationship between the score on comfort and the overall score at the 0.01 level than the level of significance, we a relationship between the score on amenities and the overall score at the 0.01 level than the level of significance, we a relationship between the score on in-house dining and the overall score at the Enter a coefficient of zero for any independent variable you chose to remove. y^=+x1+x2+x3 Create a similar scatter chart in Excel of months since last service and repair time in hours for which the points representing repairs by Bob Jones and Donna Newton are shown in different shapes and or colors. Choose the correct chart below. given the number of months since the last maintenance service and the type of repair. Let x1 represent the number of months since the last maintenance service. Let x2 represent the type of repair (a dummy variable). y^=+x1+x2 What are the interpretations of the estimated regression parameters? if we hold the type of repair constant and have a 1 month increase in the number of months since the last maintenance service. What is the coefficient of determination? If required, round your answers to four decimal places. Interpret the coefficient of determination. If required, round your answer to one decimal place. This regression model explains approximately % of the variation in the values of repair time in the sample. time, given the number of months since the last maintenance service and the repairperson. Let x1 represent the number of months since the last maintenance service. Let x2 represent the repairperson (a dummy variable). y^ - Do these charts and the results of your residual analysis suggest the same potential modifications to your simple linear regression model? given the number of months since the last maintenance service and the type of repair. Let x1 represent the number of months since the last maintenance service. Let x2 represent the type of repair (a dummy variable). y^=+x1+x2 an overall score of 94.8 , the highest component of which is 100.0 for amenities. If required, round your answers to three decimal places. Click on the datafile logo to reference the data. DATA Let x1 represent Comfort. and then sort the copied output using Excel's sorting tools. If required, round your answers to four decimal places. For subtractive or negative numbers use a minus sign. simple linear regression model? regression model. regression model. model. repairs made by Bob Jones typically have negative residuals. The results suggest that the use of dummy variables is not needed. of repair constant and the repairperson is Bob Jones. What is the coefficient of determination? If required, round your answers to four decimal places. Interpret the coefficient of determination. If required, round your answer to one decimal place. This regression model explains approximately % of the variation in the values of repair time in the sample. (f) Which of these models would you use? Why? (i) The preferred model is the one with the lowest coefficient of determination, so the best model to use is in part (c). (ii) The preferred model is the one with the lowest coefficient of determination, so the best model to use is in part (d). (iii) The preferred model is the simplest that works well, so the best model to use is in part (c). (iv) The preferred model is the one with the highest coefficient of determination, so the best model to use is in part (c). (v) The preferred model is the one with the highest coefficient of determination, so the best model to use is in part (d). time, given the number of months since the last maintenance service and the repairperson. Let x1 represent the number of months since the last maintenance service. Let x2 represent the repairperson (a dummy variable). y^=+x1+x2 What are the interpretations of the estimated regression parameters? What is the coefficient of determination? If required, round your answers to four decimal places. Interpret the coefficient of determination. If required, round your answer to one decimal place. This regression model explains approximately % of the variation in the values of repair time in the sample. Let x1 represent the number of months since the last maintenance service. Let x2 represent the type of repair (a dummy variable). Let x3 represent the repairperson (a dummy variable). Let x1 represent the number of months since the last maintenance service. Let x2 represent the type of repair (a dummy variable). Let x3 represent the repairperson (a dummy variable). y^=+x1+x2+x3 What are the interpretations of the estimated regression parameters? mechanical. is Donna Newton. of repair constant and the repairperson is Bob Jones. What is the coefficient of determination? If required, round your answers to four decimal places. Interpret the coefficient of determination. If required, round your answer to one decimal place. This regression model explains approximately % of the variation in the values of repair time in the sample. Which of these models would you use? Why? (i) The preferred model is the one with the lowest coefficient of determination, so the best model to use is in part (c). Create a similar scatter chart in Excel of months since last service and repair time in hours for which the points representing repairs by Bob Jones and Donna Newton are shown in different shapes and or colors. Choose the correct chart below. (a) Determine the estimated multiple linear regression equation that can be used to predict the overall score given the scores for comfort, amenities, and in-house dining. Let x1 represent Comfort. Let x2 represent Amenities. Let x3 represent In-House Dining. y^=+x1+x2+x3 The p-value associated with the estimated regression parameter b1 is the hypothesis that 1=0. We conclude that there of significance when controlling for The p-value associated with the estimated regression parameter b2 is the hypothesis that 2=0. We conclude that there of significance when controlling for The p-value associated with the estimated regression parameter b3 is the hypothesis that 3=0. We conclude that there Because this p-value is Because this p-value is . Because this p-value is Because this p-value is ( 0.01 level of significance when controlling for than the level of significance, we a relationship between the score on comfort and the overall score at the 0.01 level than the level of significance, we a relationship between the score on amenities and the overall score at the 0.01 level than the level of significance, we a relationship between the score on in-house dining and the overall score at the Enter a coefficient of zero for any independent variable you chose to remove. y^=+x1+x2+x3 Create a similar scatter chart in Excel of months since last service and repair time in hours for which the points representing repairs by Bob Jones and Donna Newton are shown in different shapes and or colors. Choose the correct chart below. given the number of months since the last maintenance service and the type of repair. Let x1 represent the number of months since the last maintenance service. Let x2 represent the type of repair (a dummy variable). y^=+x1+x2 What are the interpretations of the estimated regression parameters? if we hold the type of repair constant and have a 1 month increase in the number of months since the last maintenance service. What is the coefficient of determination? If required, round your answers to four decimal places. Interpret the coefficient of determination. If required, round your answer to one decimal place. This regression model explains approximately % of the variation in the values of repair time in the sample. time, given the number of months since the last maintenance service and the repairperson. Let x1 represent the number of months since the last maintenance service. Let x2 represent the repairperson (a dummy variable). y^ - Do these charts and the results of your residual analysis suggest the same potential modifications to your simple linear regression model? given the number of months since the last maintenance service and the type of repair. Let x1 represent the number of months since the last maintenance service. Let x2 represent the type of repair (a dummy variable). y^=+x1+x2
an overall score of 94.8 , the highest component of which is 100.0 for amenities. If required, round your answers to three decimal places. Click on the datafile logo to reference the data. DATA Let x1 represent Comfort. and then sort the copied output using Excel's sorting tools. If required, round your answers to four decimal places. For subtractive or negative numbers use a minus sign. simple linear regression model? regression model. regression model. model. repairs made by Bob Jones typically have negative residuals. The results suggest that the use of dummy variables is not needed. of repair constant and the repairperson is Bob Jones. What is the coefficient of determination? If required, round your answers to four decimal places. Interpret the coefficient of determination. If required, round your answer to one decimal place. This regression model explains approximately % of the variation in the values of repair time in the sample. (f) Which of these models would you use? Why? (i) The preferred model is the one with the lowest coefficient of determination, so the best model to use is in part (c). (ii) The preferred model is the one with the lowest coefficient of determination, so the best model to use is in part (d). (iii) The preferred model is the simplest that works well, so the best model to use is in part (c). (iv) The preferred model is the one with the highest coefficient of determination, so the best model to use is in part (c). (v) The preferred model is the one with the highest coefficient of determination, so the best model to use is in part (d). time, given the number of months since the last maintenance service and the repairperson. Let x1 represent the number of months since the last maintenance service. Let x2 represent the repairperson (a dummy variable). y^=+x1+x2 What are the interpretations of the estimated regression parameters? What is the coefficient of determination? If required, round your answers to four decimal places. Interpret the coefficient of determination. If required, round your answer to one decimal place. This regression model explains approximately % of the variation in the values of repair time in the sample. Let x1 represent the number of months since the last maintenance service. Let x2 represent the type of repair (a dummy variable). Let x3 represent the repairperson (a dummy variable). Let x1 represent the number of months since the last maintenance service. Let x2 represent the type of repair (a dummy variable). Let x3 represent the repairperson (a dummy variable). y^=+x1+x2+x3 What are the interpretations of the estimated regression parameters? mechanical. is Donna Newton. of repair constant and the repairperson is Bob Jones. What is the coefficient of determination? If required, round your answers to four decimal places. Interpret the coefficient of determination. If required, round your answer to one decimal place. This regression model explains approximately % of the variation in the values of repair time in the sample. Which of these models would you use? Why? (i) The preferred model is the one with the lowest coefficient of determination, so the best model to use is in part (c). Create a similar scatter chart in Excel of months since last service and repair time in hours for which the points representing repairs by Bob Jones and Donna Newton are shown in different shapes and or colors. Choose the correct chart below. (a) Determine the estimated multiple linear regression equation that can be used to predict the overall score given the scores for comfort, amenities, and in-house dining. Let x1 represent Comfort. Let x2 represent Amenities. Let x3 represent In-House Dining. y^=+x1+x2+x3 The p-value associated with the estimated regression parameter b1 is the hypothesis that 1=0. We conclude that there of significance when controlling for The p-value associated with the estimated regression parameter b2 is the hypothesis that 2=0. We conclude that there of significance when controlling for The p-value associated with the estimated regression parameter b3 is the hypothesis that 3=0. We conclude that there Because this p-value is Because this p-value is . Because this p-value is Because this p-value is ( 0.01 level of significance when controlling for than the level of significance, we a relationship between the score on comfort and the overall score at the 0.01 level than the level of significance, we a relationship between the score on amenities and the overall score at the 0.01 level than the level of significance, we a relationship between the score on in-house dining and the overall score at the Enter a coefficient of zero for any independent variable you chose to remove. y^=+x1+x2+x3 Create a similar scatter chart in Excel of months since last service and repair time in hours for which the points representing repairs by Bob Jones and Donna Newton are shown in different shapes and or colors. Choose the correct chart below. given the number of months since the last maintenance service and the type of repair. Let x1 represent the number of months since the last maintenance service. Let x2 represent the type of repair (a dummy variable). y^=+x1+x2 What are the interpretations of the estimated regression parameters? if we hold the type of repair constant and have a 1 month increase in the number of months since the last maintenance service. What is the coefficient of determination? If required, round your answers to four decimal places. Interpret the coefficient of determination. If required, round your answer to one decimal place. This regression model explains approximately % of the variation in the values of repair time in the sample. time, given the number of months since the last maintenance service and the repairperson. Let x1 represent the number of months since the last maintenance service. Let x2 represent the repairperson (a dummy variable). y^ - Do these charts and the results of your residual analysis suggest the same potential modifications to your simple linear regression model? given the number of months since the last maintenance service and the type of repair. Let x1 represent the number of months since the last maintenance service. Let x2 represent the type of repair (a dummy variable). y^=+x1+x2 an overall score of 94.8 , the highest component of which is 100.0 for amenities. If required, round your answers to three decimal places. Click on the datafile logo to reference the data. DATA Let x1 represent Comfort. and then sort the copied output using Excel's sorting tools. If required, round your answers to four decimal places. For subtractive or negative numbers use a minus sign. simple linear regression model? regression model. regression model. model. repairs made by Bob Jones typically have negative residuals. The results suggest that the use of dummy variables is not needed. of repair constant and the repairperson is Bob Jones. What is the coefficient of determination? If required, round your answers to four decimal places. Interpret the coefficient of determination. If required, round your answer to one decimal place. This regression model explains approximately % of the variation in the values of repair time in the sample. (f) Which of these models would you use? Why? (i) The preferred model is the one with the lowest coefficient of determination, so the best model to use is in part (c). (ii) The preferred model is the one with the lowest coefficient of determination, so the best model to use is in part (d). (iii) The preferred model is the simplest that works well, so the best model to use is in part (c). (iv) The preferred model is the one with the highest coefficient of determination, so the best model to use is in part (c). (v) The preferred model is the one with the highest coefficient of determination, so the best model to use is in part (d). time, given the number of months since the last maintenance service and the repairperson. Let x1 represent the number of months since the last maintenance service. Let x2 represent the repairperson (a dummy variable). y^=+x1+x2 What are the interpretations of the estimated regression parameters? What is the coefficient of determination? If required, round your answers to four decimal places. Interpret the coefficient of determination. If required, round your answer to one decimal place. This regression model explains approximately % of the variation in the values of repair time in the sample. Let x1 represent the number of months since the last maintenance service. Let x2 represent the type of repair (a dummy variable). Let x3 represent the repairperson (a dummy variable). Let x1 represent the number of months since the last maintenance service. Let x2 represent the type of repair (a dummy variable). Let x3 represent the repairperson (a dummy variable). y^=+x1+x2+x3 What are the interpretations of the estimated regression parameters? mechanical. is Donna Newton. of repair constant and the repairperson is Bob Jones. What is the coefficient of determination? If required, round your answers to four decimal places. Interpret the coefficient of determination. If required, round your answer to one decimal place. This regression model explains approximately % of the variation in the values of repair time in the sample. Which of these models would you use? Why? (i) The preferred model is the one with the lowest coefficient of determination, so the best model to use is in part (c). Create a similar scatter chart in Excel of months since last service and repair time in hours for which the points representing repairs by Bob Jones and Donna Newton are shown in different shapes and or colors. Choose the correct chart below. (a) Determine the estimated multiple linear regression equation that can be used to predict the overall score given the scores for comfort, amenities, and in-house dining. Let x1 represent Comfort. Let x2 represent Amenities. Let x3 represent In-House Dining. y^=+x1+x2+x3 The p-value associated with the estimated regression parameter b1 is the hypothesis that 1=0. We conclude that there of significance when controlling for The p-value associated with the estimated regression parameter b2 is the hypothesis that 2=0. We conclude that there of significance when controlling for The p-value associated with the estimated regression parameter b3 is the hypothesis that 3=0. We conclude that there Because this p-value is Because this p-value is . Because this p-value is Because this p-value is ( 0.01 level of significance when controlling for than the level of significance, we a relationship between the score on comfort and the overall score at the 0.01 level than the level of significance, we a relationship between the score on amenities and the overall score at the 0.01 level than the level of significance, we a relationship between the score on in-house dining and the overall score at the Enter a coefficient of zero for any independent variable you chose to remove. y^=+x1+x2+x3 Create a similar scatter chart in Excel of months since last service and repair time in hours for which the points representing repairs by Bob Jones and Donna Newton are shown in different shapes and or colors. Choose the correct chart below. given the number of months since the last maintenance service and the type of repair. Let x1 represent the number of months since the last maintenance service. Let x2 represent the type of repair (a dummy variable). y^=+x1+x2 What are the interpretations of the estimated regression parameters? if we hold the type of repair constant and have a 1 month increase in the number of months since the last maintenance service. What is the coefficient of determination? If required, round your answers to four decimal places. Interpret the coefficient of determination. If required, round your answer to one decimal place. This regression model explains approximately % of the variation in the values of repair time in the sample. time, given the number of months since the last maintenance service and the repairperson. Let x1 represent the number of months since the last maintenance service. Let x2 represent the repairperson (a dummy variable). y^ - Do these charts and the results of your residual analysis suggest the same potential modifications to your simple linear regression model? given the number of months since the last maintenance service and the type of repair. Let x1 represent the number of months since the last maintenance service. Let x2 represent the type of repair (a dummy variable). y^=+x1+x2 Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


