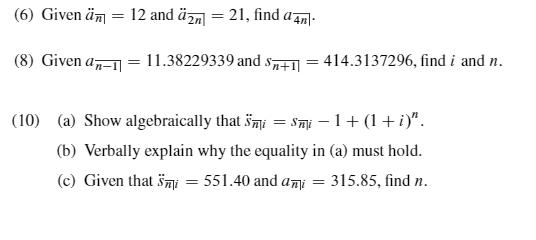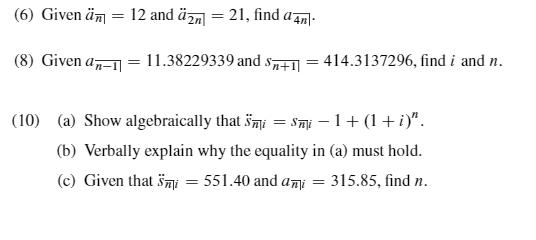



ANNUITIES -DUE questions
Questions from BookChapter 3 section 3 of Mathematical Interest Theory, 2nd Edition by J. Daniel and L. Vaaler, Pearson
(E) Given Jim :12 and fig 2 2L nd "El- (8) Given al = 113322933de am 2 4143131296, nd .r' and n. (ID) (a) Shaw algebraically [hat Sim; 2.5311- l -l (l + H". (b) 1lllea'ljally explain why the equality in (a) must hold. (c) Given that 55m,- = 551.40 and am;- 2 315.35, nd a. 3.3 ANNUI'I'IES-DUE An annuity lasting 11 interest peri nds with payments at the beginning et' eaeh interest perind is called an annuity-due. By a basis annuity-due, we mean an annuitydue 124 Chapter 3 Annuities {annuities certain} with level payments, each el' which is equal to I. The value at a given time nfa level ann uitydue with payments ef Q is just Q times the value at the basin annuitydue. Having xed a ehniee nf aeeumnlatien funetien 151(1). let m denete the value at the time ef the rst payment nf the basic annuitydue that lasts 11 perinds, and write Em fer the value at the end ef the nth payment peried ef this annuity. Hate that time 11 is one peried after the nal payment of an annuitydue with duratien 1r perieds. If the ehnsen aeeu mnlatien funetien is the enmpnund interest aeeumulatinn funetien n} = [l + if, the symhel fish- is enmmnnly used fer the value at the time 1:11" the rst payment. and the symhnl Em; indicates the value at time 11. The annuity symhnl ilr' is read "a dnuhledet, angle .11., at interest rate 1'" er "a due, angle a, at interest rate 1' ." Likewise. Ea"- is "s dnuhledet. angle 11, at interest rate 1'" er "5 due. angle a, at interest rate i." PAYMENT: I 1 1 1 1 TIME: 11 1 2 3 1'1 1 1r VALUE: as. sea FIGURE {3.3.1} Analegnusly tn (3.2.3) and {3.2.9}. we have [3.3.2] and mere generally. (3.3.31 a" = .21an and an = 1:111:13". IHPDFITAHT FACT {3.3.4} With an annuitydue. ycu start receiving payments immediately. The value cf a basic annuity-due lasting a perinds at the time cf the rst payment is dencted by ail. The last payment is made at the beginning cf the nth peri cd. and Em gives the annuity's value cne pericd after this last payment. that is tc say at the end cf the uth pericd. The annuity symbcl Eigh- is given by a geometric series. the sum cf which may be cnmputed using {3.2.2}. Recalling that l u = sf (Equatic-n LEW}, we nd (3.3.5) A t'c-rmula fer the annuity sy mbcl sin-=13 +.']"+.:1+.')"*'+(1+:}"'2 +---+.:1+:]p1 ean alse he eemputed using the fenuula fer summing a geemetrie series {3.2.2}, but it is semewhat simpler te use (3.3.2) and {3.3.5}. Due arrives at am.- =(1+t}"+{1+t}"1 +tl+c'}"""*+---+tl+-'i}l (3'15) _ t1+:'}"1 _ T' Nete that the fermula fer the present value iii"- given in {3.3.5} is the same as the fermula fer the present value "tr' presented in (3.14} exeept that in the fermula fer the annuitydue there is a If in the deneminater, while the equatien fer the annuity immediate has an i . There is a similar statement fer the aeeumulated values. Perhaps yeu will nd the fellewing memery aid helpful. The we "immediate" begins with the letter "i" and the annuity symhels fer a hasie annuityimmediate have an "t" in the deneminater. In eentrmt, "due" begins with "d" and the annuity symhels fer a hasie annuitydue have a "d" in the deneminater. The symhelsmf and 55in are elesely related te the symhelsnm; and Siu- Since fian- measures the value ef an npayment hasie annuity at the time ef the rst payment. and um,- measures the value ef an npayment hasie annuity ene peried hefere the rst payment. Similarly. There is a seeend type ef relatienship between the annuityimmediate symhels and the annuitydue symhels. The annuity symhel iii"- measures the value at time D ef payments ef 1 made at times t}, 1.1.... n l , while the annuity symhel emi- measures the value at time t} ef payments efl made at times 1.2, . . .,n 1. Se, these twe symhels give the time t] value ef the same series ef payments, exeept that aim;- ineludes the value ef an additienal payment ef I at time t]. Therefere {3.3.9} Em;- = an; + 1. Similarly. [3.3.1{1} Eat: + 1 = 3n+1i~ . -I I" . I"