answer all cc

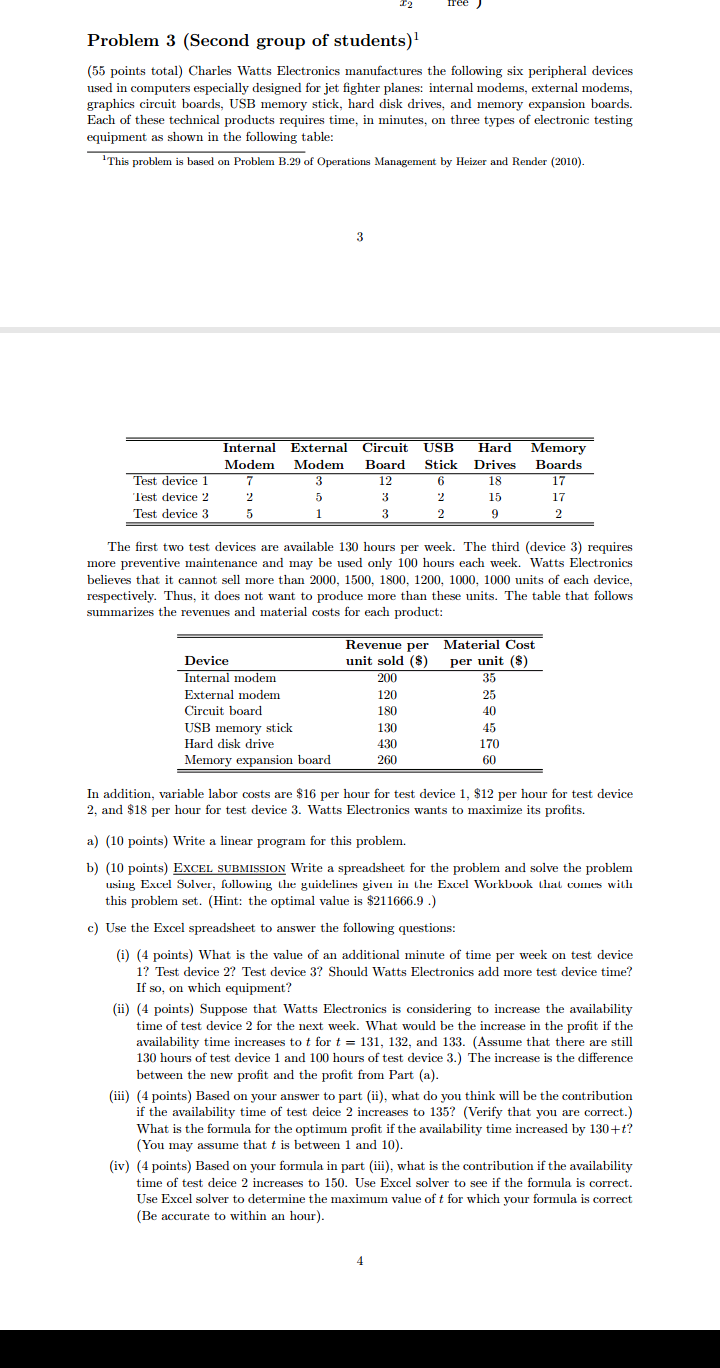
Question 1: Solow Model (40 points) i. ii. In 3-4 pages, in your own words, delve into a detailed discussion of the three variations of the Solow growth model (the basic Solow model, Solow model with population growth and the Solow model with technological progress). Be sure to explain the relevant equations that form the foundation of each model as well as the predictions for the three variations of the model. In your judgement, how useful (or not) is the Solow model as an analytic tool for understanding the differences in developing and developed countries? (1-2 pages) 3. Solow Growth Model with Technological Progress State the basic assumptions of the Solow model with technological change and derive expression for income per worker y(t) in the steady state of this model. Use the Solow diagram to explain why the economy converges to its steady state. Human Capital: Our textbook points out that human capital is not included in the simple model of production but that it could be an important factor in explaining why the marginal product of capital differs among countries. 1. Consider a Cobb-Douglas production function with three inputs: Y = KiLiHi, (1) where K is capital, L is labor, and H is human capital. What is the marginal product of capital (MPK) implied by this production function? 2. Is MPK increasing in human capital or decreasing? 3. Use this model to explain why capital may flow from poor to rich countries. 4. Is the return to education higher or lower in countries with scarce capital?Question 2: Capital formation in growth models 10 points each sub-part equally weighted 1.Derive the growth equation for Harrod Domar model. 2. Derive the capital formation equation for Solow model with and without labor augmenting technological progress. 3.Derive the human capital formation equation for the following production function Y = HOK'(TL)1-a-B where Y is output, H is human capital in the production function, K is physical capital used in the production function and L is labor. The saving rate in human capital is given by s.Problem 3 (Second group of students)' (55 points total) Charles Watts Electronics manufactures the following six peripheral devices used in computers especially designed for jet fighter planes: internal modems, external modems, graphics circuit boards, USB memory stick, hard disk drives, and memory expansion boards. Each of these technical products requires time, in minutes, on three types of electronic testing equipment as shown in the following table: `This problem is based on Problem B.29 of Operations Management by Heizer and Render (2010). Internal External Circuit USB Hard Memory Modem Modem Board Stick Drives Boards Test device 1 12 18 17 Test device 2 15 17 Test device 3 2 The first two test devices are available 130 hours per week. The third (device 3) requires more preventive maintenance and may be used only 100 hours each week. Watts Electronics believes that it cannot sell more than 2000, 1500, 1800, 1200, 1000, 1000 units of each device, respectively. Thus, it does not want to produce more than these units. The table that follows summarizes the revenues and material costs for each product: Revenue per Material Cost Device unit sold ($) per unit ($) Internal modem 200 35 External modem 120 25 Circuit board 180 40 USB memory stick 130 45 Hard disk drive 430 170 Memory expansion board 260 60 In addition, variable labor costs are $16 per hour for test device 1, $12 per hour for test device 2, and $18 per hour for test device 3. Watts Electronics wants to maximize its profits. a) (10 points) Write a linear program for this problem. b) (10 points) EXCEL SUBMISSION Write a spreadsheet for the problem and solve the problem using Excel Solver, following the guidelines given in the Excel Workbook that comes with this problem set. (Hint: the optimal value is $211666.9 .) c) Use the Excel spreadsheet to answer the following questions: (i) (4 points) What is the value of an additional minute of time per week on test device 1? Test device 2? Test device 3? Should Watts Electronics add more test device time? If so, on which equipment? (ii) (4 points) Suppose that Watts Electronics is considering to increase the availability time of test device 2 for the next week. What would be the increase in the profit if the availability time increases to t for t = 131, 132, and 133. (Assume that there are still 130 hours of test device 1 and 100 hours of test device 3.) The increase is the difference between the new profit and the profit from Part (a) (iii) (4 points) Based on your answer to part (ii), what do you think will be the contribution if the availability time of test deice 2 increases to 135? (Verify that you are correct.) What is the formula for the optimum profit if the availability time increased by 130+t? (You may assume that t is between 1 and 10). (iv) (4 points) Based on your formula in part (ii), what is the contribution if the availability time of test deice 2 increases to 150. Use Excel solver to see if the formula is correct. Use Excel solver to determine the maximum value of t for which your formula is correct (Be accurate to within an hour).(v) (4 points) How would the optimal solution in Part (b) change if the labor costs increased to $18 per hour for test device 1, $13 per hour for test device 2, and $20 per hour for test device 3? (vi) (5 points) Over what range of the labor cost for test device 3 will the optimal production- mix in Part (b) remain optimal? (Be accurate to within one dollar.) d) (10 points) Write an algebraic formulation for the problem using the following notation: . m is the number of peripheral devices, . n is the number of test devices, . a, is the maximum availability time of test device i ( in hour), . c' is the labor cost per hour of test device i (in $), . ca is the material cost per unit for device j (in $), . r; is the revenue cost per unit for device j (in $), . b; is the maximum availability of material j, . gij is the amount of time in minute on test service i that is required in device j,Homework 1 Due on 9/25/2012 1. Consider a homeowner with Von-Neumann and Morgenstern utility function u, where u(x) = 1 -e" for wealth level z, measured in million US dollars. His entire wealth is his house. The value of a house is 1 (million US dollars), but the house can be destroyed by a flood, reducing its value to 0, with probability # E (0, 1). (a) What is the largest premium P is the homeowner is willing to pay for a full insurance? (He pays the premium P and gets back 1 in case of a flood, making his wealth 1 - P regardless of the flood.) (b) Suppose there is a local insurance company who has insured n houses, all in his neighborhood, for premium P. Suppose also that with probability a there can be flood in the neighborhood destroying all houses (i.e., either all houses are destroyed or none of them is destroyed). Suppose finally that P is small enough that the homeowner has insured is house. Having insured his house, what is the largest Q that he is willing to pay to get the 1 share of the company? (The value of the company is the total premium it collects minus the payments to the insured homeowners in case of a flood.) (c) Answer part (b) assuming now that the insurance company is global. It insured n houses in different parts of the world (all outside of his neighborhood), so that the destruction of houses by flood are all independent (i.e., the probability of flood in one house is a independent of how many other houses has been flooded). (d) Assume that n is large enough so that Etz Chet/"* (1 - ,)"- 2 (*+#(1-=)/(2). discuss your answers to above questions (briefly). [Here, C, denotes the number of k combinations out of n, and the sum is one minus the expected payoff from the loss due to the payments to the flooded houses.] 2. Consider the game in which the following are commonly known. First, Ann chooses between actions a and 6. Then, with probability 1/3, Bob observes which action Ann has chosen and with probability 2/3 he does not observe the action she has chosen. In all cases (regardless of whether he has observed Ann chose a, or he has observed Ann chose b, or he has not observed any action), Bob chooses between actions a and B. The payoff of each player is 1 after (a, a) and (b. 8) and 0 otherwise. (a) Write the above game in extensive form. (b) Write the above game in normal form. 3. Consider the following variation of the above game. First, Ann chooses between actions a and b. Then, Bob decides whether to observe the chosen action of Ann or not, by choosing between the actions Open and Shut, respectively. In all cases, Bob then chooses between actions o and B. The payoff of Ann is 1 after (a, c) and (b. ) and 0 otherwise, regardless of whether Bob chooses Open or Shut. The payoff of Bob is equal to the payoff of Ann if he has chosen Shut, and his payoff is equal to the payoff of Ann minus 1/2 if he has chosen Open. (a) Write the above game in extensive form. (b) Write the above game in normal form. 4. Federal government is planning to build an interstate highway between two states, named A and B. The highway costs C > 0 to the government, and the value of the highway to the states A and B are va 2 0 and up 2 0, respectively. Simultaneously, each state i E { A, B } is to bid by E [0, co). If ba + ba 2 C the highway is constructed. For any distinct i, j E {A, B}, state i pays C - b, to the federal government if by