Answer all the questions accordingly
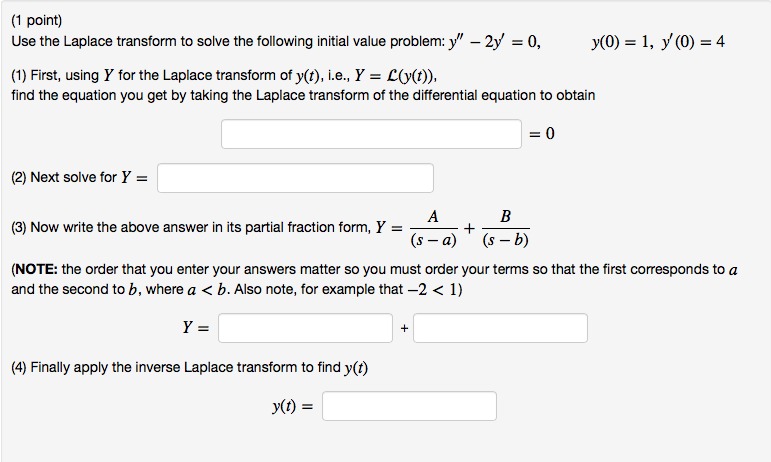
Problem 1 Suppose a sequence of random variables is generated as follows. Let X] ~ uniform(0, 1), and X2 X] ~ uniform(X1, 1). In general, let Xxtil(X1, ..., Xx) ~ uniform (Xk, 1). (a) Find the joint density of (- log(1 - X1), - log(1 - X2)) by using bivariate trans- formations. Be sure to specify the support of this density. (b) Find the marginal density of - log(1 - X2). (c) Find the conditional density of X2 given (X1, X3). What about X2 given (X1, X3, X4, ..., X20 (d) Find EXe, k = 1,2,... by using the law of iterated conditional expectations. (Hint: you may find it easier to work with E(1 - Xk).) (e) Prove that Xx - 1 in probability as k -> co.Nationally, patients who go to the emergency room wait an average of 6 hours to be admitted into the hospital. Do patients at rural hospitals have a higher waiting time? The 15 randomly selected patients who went to the emergency room at rural hospitals waited an average of 6.2 hours to be admitted into the hospital. The standard deviation for these 15 patients was 2 hours. What can be concluded at the the a = 0.10 level of significance level of significance? a. For this study, we should use Select an answer b. The null and alternative hypotheses would be: Ho: Select an answer Select an answer C. The test statistic 7 (please show your answer to 3 decimal places.) d. The p-value = [Please show your answer to 4 decimal places.) e. The p-value is 7 + a f. Based on this, we should Soloct an answer the null hypothesis. g. Thus, the final conclusion is that ... The data suggest the populaton mean is significantly higher than 6 at a = 0.10, so there is statistically significant evidence to conclude that the population mean waiting time to be admitted into the hospital from the emergency room for patients at rural hospitals is higher than 6 hours. The data suggest the population mean is not significantly higher than 6 at a = 0.10, so there is statistically insignificant evidence to conclude that the population mean waiting time to be admitted into the hospital from the emergency room for patients at rural hospitals is equal to 6 hours. The data suggest that the population mean awaiting time to be admitted into the hospital from the emergency room for patients at rural hospitals is not significantly higher than 6 hours at or = 0.10, so there is statistically insignificant evidence to conclude that the population mean waiting time to be admitted into the hospital from the emergency room for patients at rural hospitals is higher than 6 hours.Problem 2. (1) Let X1, X2, . .. be a sequence of independent and identically distributed random variables, each following the exponential distribution with parameter o. Let / be another independent random variable following a Pois- son distribution with parameter A. What is the moment generating function of X1+ ... + XN? (2) Let U1, U2, . .. be a sequence of independent random variables uniformly dis- tributed over [0, 1]. Let N be another independent random variable whose prob- ability mass function is given by P(N = n) = (e - 1)n!' n = 1, 2. . .. . Define X = max(U1, . . . , UN). (2-i) Find the cumulative distribution function and probability density function of max(U1, U2, U3). (2-ii) What is the moment generating function of X? (2-iii) Let R be another independent random variable whose probability mass function is given by P(R= r) = (e - 1 )e ", r =1,2, .... What is the distribution of R - X?4. (20 points.) All: Apply a "finite-difference" method to discretize the following model equation a(UT) aT P K OX ox Where f and u are known functions at all grid points; p is constant and K is the thermal conductivity which varies with x. What is the accuracy of your finite difference equations (you can just state the truncation error and derivation is not needed)?['I point} Use the Laplace transform to solve the following initial value problem: 3:\" 2y' = I}. yin) = 1' y' (B) = 4 [1} First, using I" for the Laplace transfom'l of t), i.e., Y = [y(f)). find the equation you get by taking the Laplace transform of the differential equation to obtain = [2) Next solve for Y = A + B (s - a) (3 - 1}) [NOTE the order that you enter your answers matter so you must order your terms so that the first corresponds to a and the second to b. where a
