Answer ALL the questions please. I will provide a good rating. Screenshots attached below. Questions 1-4.
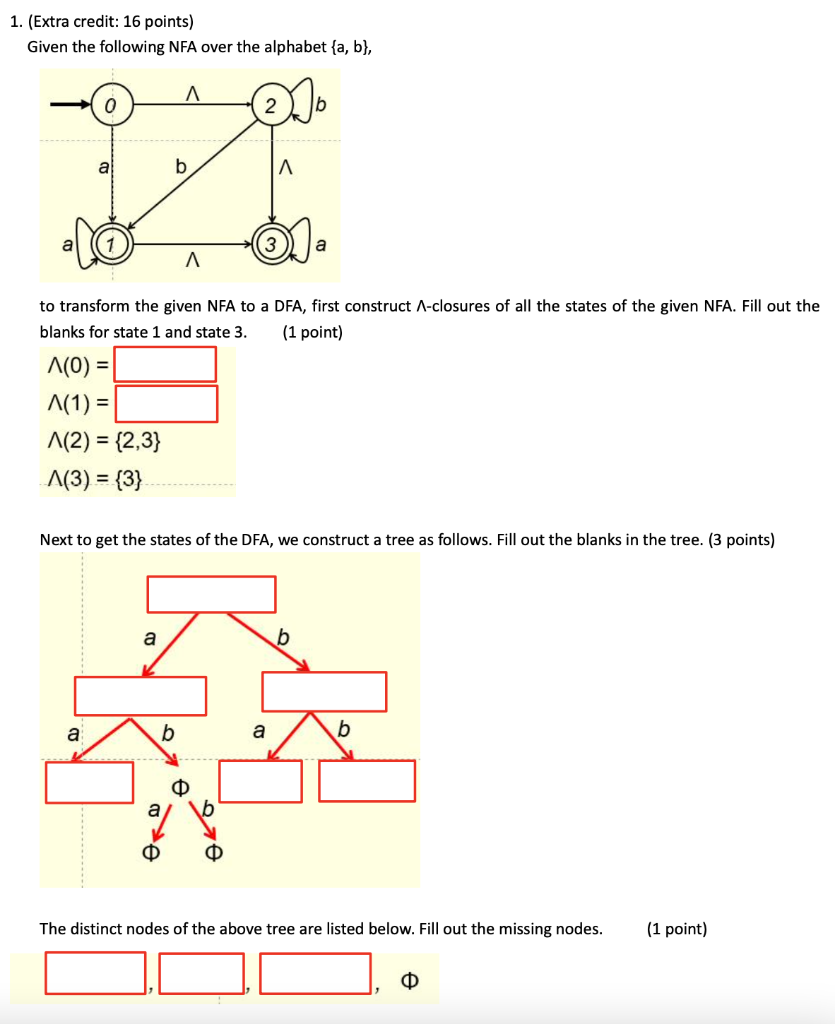
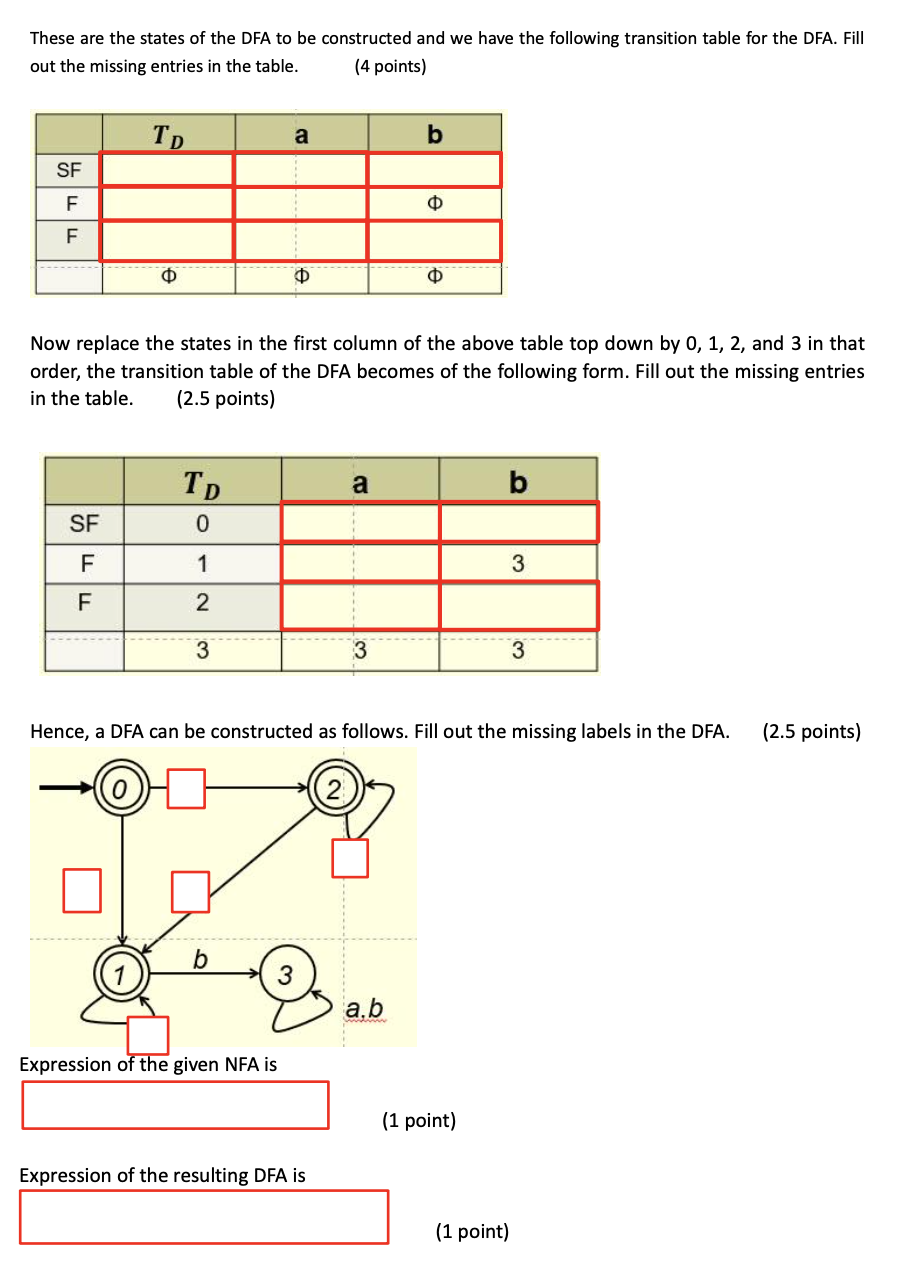
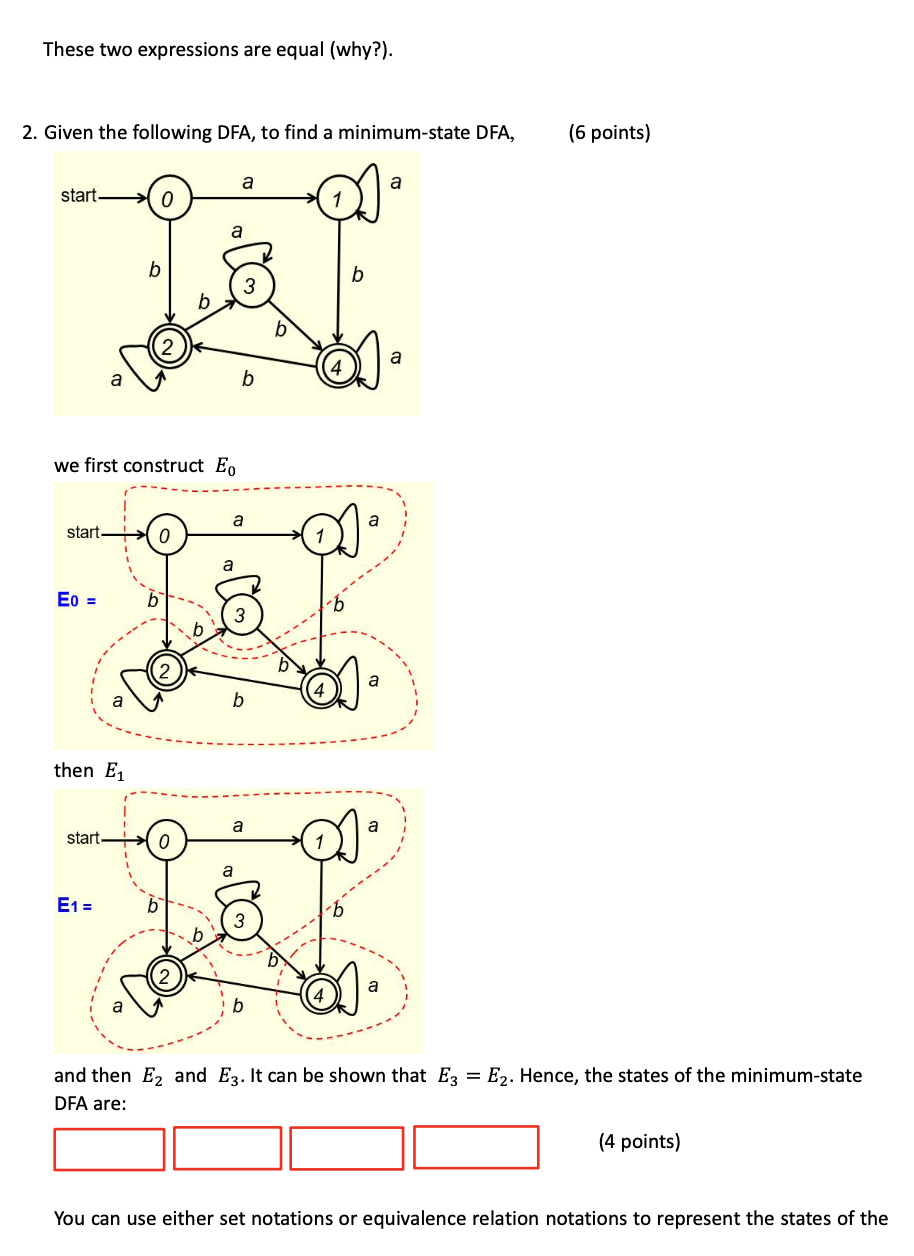

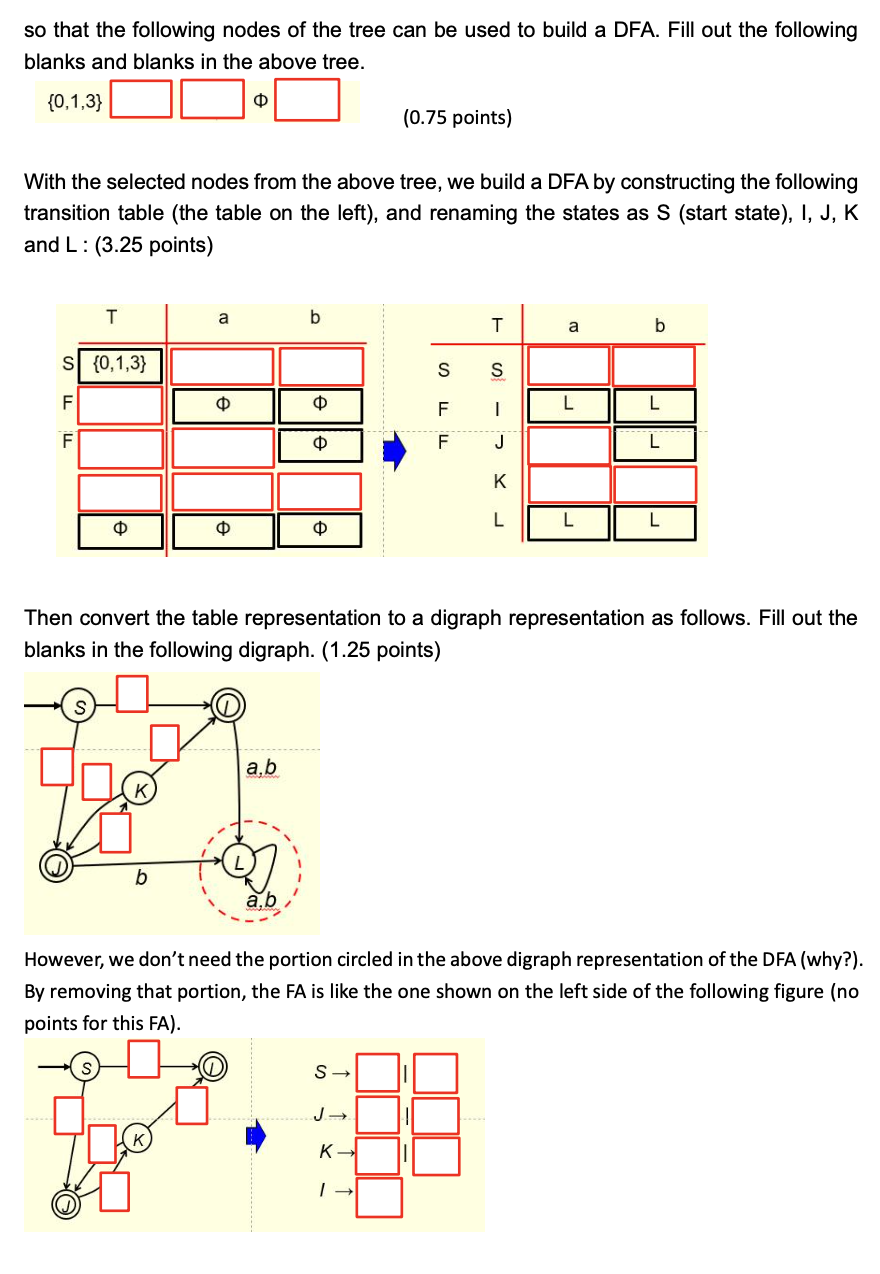

1. (Extra credit: 16 points) Given the following NFA over the alphabet {a,b}, to transform the given NFA to a DFA, first construct -closures of all the states of the given NFA. Fill out the blanks for state 1 and state 3. (1 point) (0)=(1)=(2)={2,3}(3)={3} Next to get the states of the DFA, we construct a tree as follows. Fill out the blanks in the tree. ( 3 points) The distinct nodes of the above tree are listed below. Fill out the missing nodes. (1 point) These are the states of the DFA to be constructed and we have the following transition table for the DFA. Fill out the missing entries in the table. (4 points) Now replace the states in the first column of the above table top down by 0,1,2, and 3 in that order, the transition table of the DFA becomes of the following form. Fill out the missing entries in the table. (2.5 points) Hence, a DFA can be constructed as follows. Fill out the missing labels in the DFA. (2.5 points) Expression of the given NFA is (1 point) Expression of the resulting DFA is These two expressions are equal (why?). 2. Given the following DFA, to find a minimum-state DFA, (6 points) we first construct E0 then E1 and then E2 and E3. It can be shown that E3=E2. Hence, the states of the minimum-state DFA are: (4 points) You can use either set notations or equivalence relation notations to represent the states of the minimum-state DFA. The start state is: The final state is: (2 points) 3. Let the set of states for a DFA be S={0,1,2,3,4,5}, where the start state is 0 and the final states are 3,4 and 5 . Let the equivalence relation on S for a minimum-state DFA be generated by the following set of equivalent pairs of states: {(0,2),(3,4)} The states of the minimum-state DFA are: (2 points) (set notations) or (equivalence class notations) You only need to answer one of the above two cases. 4. (12 points) Given the following regular expression over the alphabet {a,b}, (ba)*(a+b) to transform it to a regular grammar, we first transform it to an NFA as the one shown below. Instead of converting this NFA to a regular grammar directly, we convert it to a DFA first and then convert the DFA to a regular grammar (why?). So we construct -closures of the above NFA, (0)={0,1,3}(1)={1,3}(2)={2}(3)={3}(4)={4}()= and build the following tree, ( 3 points) so that the following nodes of the tree can be used to build a DFA. Fill out the following blanks and blanks in the above tree. {0,1,3} ( 0.75 points) With the selected nodes from the above tree, we build a DFA by constructing the following transition table (the table on the left), and renaming the states as S (start state), I, J, K and L : (3.25 points) Then convert the table representation to a digraph representation as follows. Fill out the blanks in the following digraph. (1.25 points) However, we don't need the portion circled in the above digraph representation of the DFA (why?). By removing that portion, the FA is like the one shown on the left side of the following figure (no points for this FA). By constructing production rules from this FA, we get the production set of the regular grammar on the right side of the above figure. Fill out the blanks in the above figure. (1.75 points for the production set) Regular expression of the above FA is (2 points) which is equal to the given regular expression (ba)*(a+b). (Why?)












