answer asappp

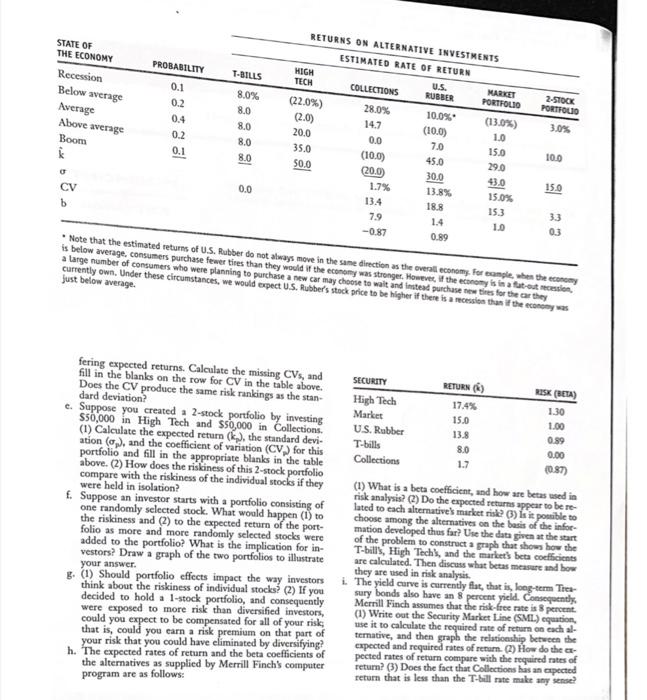
a. Use the data given to calculate annual returns for Bartman, Reynolds, and the Wiltor 5000 Index, and then calculate average returns over the 5-year period. (Hint: Remember returns are calculated by subtracting the beginning price from the ending price to get the capital gain or loss, adding the dividend to the capital gain or loss, and dividing the resul by the beginning price. Assume that dividends are already included in the index. Also, you cannot calculate the rate of return for 1996 because you do not have 1995 data.) b. Calculate the standard deviations of the returns for Bartman, Reynolds, and the Wiltor 5000. (Hint: Use the sample standard deviation formula given in Footnote 5 to this chap ter, which corresponds to the STDEV function in Excel.) c. Now calculate the coefficients of variation for Bartman, Reynolds, and the Wilton 5000. d. Construct a scatter diagram graph that shows Bartman's and Reynolds' returns on the ver tical axis and the market index's returns on the horizontal axis. e. Estimate Bartman's and Reynolds' betas by running regressions of their returns against the Wilton 5000's returns. Are these betas consistent with your graph? f. The risk-free rate on long-term Treasury bonds is 6.04 percent. Assume that the averag annual return on the Wilton 5000 is not a good estimate of the market's required return it is too high, so use 11 percent as the expected return on the market. Now use the SMI equation to calculate the two companies' required returns. g. If you formed a portfolio that consisted of 50 percent of Bartman stock and 50 percent o Reynolds stock, what would be the beta and the required return for the portfolio? h. Suppose an investor wants to include Bartman Industries' stock in his or her portfolio Stocks A, B, and C are currently in the portfolio, and their betas are 0.769, 0.985 and 1.423, respectively. Calculate the new portfolio's required return if it consists o 25 percent of Bartman, 15 percent of Stock A, 40 percent of Stock B, and 20 percent c Stock C. INTEGRATED CASE MERRILL FINCH INC. 5-23 Risk and return Assume that you recently graduated with a major in finance, and you just landed a job as a finan- cial planner with Merrill Finch Inc., a large financial services corporation. Your first assignment is to invest $100,000 for a client. Because the funds are to be invested in a business at the end of 1 year, you have been instructed to plan for a 1- year holding period. Further, your boss has restricted you to the following investment alternatives in the table below, shown with their probabilities and associated outcomes. (Disregard for now the items at the bottom of the data; you will fill in the blanks later.) Merrill Finch's economic forecasting staff has developed probability estimates for the state of the economy, and its security analysts have developed a sophisticated computer program, which was used to estimate the rate of return on each alternative under each state of the economy. High Tech Inc. is an electronics firm; Collections Inc. collects past-due debts; and U.S. Rubber manufactures tires and various other rubber and plastics products. Merrill Finch also maintains a "market portfolio" that owns a market- weighted fraction of all publicly traded stocks; you can in- vest in that portfolio, and thus obtain average stock market results. Given the situation as described, answer the follow ing questions. a. (1) Why is the T-bill's return independent of the state ( the economy? Do T-bills promise a completely risk-fre return? (2) Why are High Tech's returns expected t move with the economy whereas Collections' are e pected to move counter to the economy? b. Calculate the expected rate of return on each alternativ and fill in the blanks on the row for k in the table belo c. You should recognize that basing a decision solely on e: pected returns is only appropriate for risk-neutral ind viduals. Since your client, like virtually everyone, is ris averse, the riskiness of each alternative is an importa aspect of the decision. One possible measure of risk is th standard deviation of returns. (1) Calculate this value fo each alternative, and fill in the blank on the row for o the table below. (2) What type of risk is measured by th standard deviation? (3) Draw a graph that shows rough the shape of the probability distributions for High Tec U.S. Rubber, and T-bills. d. Suppose you suddenly remembered that the coefficient variation (CV) is generally regarded as being a bett measure of stand-alone risk than the standard deviatic when the alternatives being considered have widely di RETURNS ON ALTERNATIVE INVESTMENTS ESTIMATED RATE OF RETURN PROBABILITY T-BILLS HIGH TECH U.S. MARKET COLLECTIONS RUBBER PORTFOLIO 2-STOCK PORTFOLIO 0.1 8.0% (22.0%) 28.0% 0.2 10.0% (13.0%) 8.0 (2.0) 14.7 (10.0) 0.4 1.0 8.0 20.0 7.0 0.2 15.0 10.0 8.0 35.0 45.0 29.0 0.1 8.0 50.0 30.0 43.0 15.0 13.8% 15.0% 0.0 18.8 15.3 CV 3.3 7.9 1.4 1.0 0.3 b -0.87 0.89 Note that the estimated returns of U.S. Rubber do not always move in the same direction as the overall economy. For example, when the economy is below average, consumers purchase fewer tires than they would if the economy was stronger. However, if the economy is in a flat-out recession, a large number of consumers who were planning to purchase a new car may choose to wait and instead purchase new tires for the car they currently own, Under these circumstances, we would expect U.S. Rubber's stock price to be higher if there is a recession than if the economy was just below average. RETURN() RISK (BETA) fering expected returns. Calculate the missing CVs, and fill in the blanks on the row for CV in the table above. Does the CV produce the same risk rankings as the stan- dard deviation? SECURITY High Tech Market 17.4% 1.30 15.0 1.00 13.8 0.89 U.S. Rubber T-bills 8.0 0.00 Collections 1.7 e. Suppose you created a 2-stock portfolio by investing $50,000 in High Tech and $50,000 in Collections. (1) Calculate the expected return (k), the standard devi- ation (o,), and the coefficient of variation (CV) for this portfolio and fill in the appropriate blanks in the table above. (2) How does the riskiness of this 2-stock portfolio compare with the riskiness of the individual stocks if they were held in isolation? (0.87) f. Suppose an investor starts with a portfolio consisting of one randomly selected stock. What would happen (1) to the riskiness and (2) to the expected return of the port- folio as more and more randomly selected stocks were added to the portfolio? What is the implication for in- vestors? Draw a graph of the two portfolios to illustrate (1) What is a beta coefficient, and how are betas used in risk analysis? (2) Do the expected returns appear to be re- lated to each alternative's market risk? (3) Is it possible to choose among the alternatives on the basis of the infor- mation developed thus far? Use the data given at the start of the problem to construct a graph that shows how the T-bill's, High Tech's, and the market's beta coefficients are calculated. Then discuss what betas measure and how they are used in risk analysis. your answer. i. g. (1) Should portfolio effects impact the way investors think about the riskiness of individual stocks? (2) If you decided to hold a 1-stock portfolio, and consequently were exposed to more risk than diversified investors, could you expect to be compensated for all of your risk that is, could you earn a risk premium on that part of your risk that you could have eliminated by diversifying? h. The expected rates of return and the beta coefficients of the alternatives as supplied by Merrill Finch's computer program are as follows: The yield curve is currently flat, that is, long-term Tres- sury bonds also have an 8 percent yield. Consequently, Merrill Finch assumes that the risk-free rate is 8 percent. (1) Write out the Security Market Line (SML) equation, use it to calculate the required rate of return on each al- ternative, and then graph the relationship between the expected and required rates of return. (2) How do the ex- pected rates of return compare with the required rates of return? (3) Does the fact that Collections has an expected return that is less than the T-bill rate make any sense? STATE OF THE ECONOMY Recession Below average Average Above average Boom k 0.0 (10,0) (20.0) 1.7% 13.4 (4) What would be the market risk and the required re- turn of a 50-50 portfolio of High Tech and Collections? Of High Tech and U.S. Rubber? j. (1) Suppose investors raised their inflation expectations by 3 percentage points over current estimates as reflected in the 8 percent risk-free rate. What effect would higher in- flation have on the SML and on the returns required on high- and low-risk securities? (2) Suppose instead that in- vestors' risk aversion increased enough to cause the market risk premium to increase by 3 percentage points. (Inflation remains constant.) What effect would this have on the SML and on returns of high- and low-risk securities? CYBER PROBLEM Please go to our web site http://brigham.swlearning.com to access the Cyberproblems. THOMSON With your Xtra! CD-ROM, access the Thomson Analytics Problems and use the Thomson Analytics Academic online database to work this chapter's problems. ANALYTICS a. Use the data given to calculate annual returns for Bartman, Reynolds, and the Wiltor 5000 Index, and then calculate average returns over the 5-year period. (Hint: Remember returns are calculated by subtracting the beginning price from the ending price to get the capital gain or loss, adding the dividend to the capital gain or loss, and dividing the resul by the beginning price. Assume that dividends are already included in the index. Also, you cannot calculate the rate of return for 1996 because you do not have 1995 data.) b. Calculate the standard deviations of the returns for Bartman, Reynolds, and the Wiltor 5000. (Hint: Use the sample standard deviation formula given in Footnote 5 to this chap ter, which corresponds to the STDEV function in Excel.) c. Now calculate the coefficients of variation for Bartman, Reynolds, and the Wilton 5000. d. Construct a scatter diagram graph that shows Bartman's and Reynolds' returns on the ver tical axis and the market index's returns on the horizontal axis. e. Estimate Bartman's and Reynolds' betas by running regressions of their returns against the Wilton 5000's returns. Are these betas consistent with your graph? f. The risk-free rate on long-term Treasury bonds is 6.04 percent. Assume that the averag annual return on the Wilton 5000 is not a good estimate of the market's required return it is too high, so use 11 percent as the expected return on the market. Now use the SMI equation to calculate the two companies' required returns. g. If you formed a portfolio that consisted of 50 percent of Bartman stock and 50 percent o Reynolds stock, what would be the beta and the required return for the portfolio? h. Suppose an investor wants to include Bartman Industries' stock in his or her portfolio Stocks A, B, and C are currently in the portfolio, and their betas are 0.769, 0.985 and 1.423, respectively. Calculate the new portfolio's required return if it consists o 25 percent of Bartman, 15 percent of Stock A, 40 percent of Stock B, and 20 percent c Stock C. INTEGRATED CASE MERRILL FINCH INC. 5-23 Risk and return Assume that you recently graduated with a major in finance, and you just landed a job as a finan- cial planner with Merrill Finch Inc., a large financial services corporation. Your first assignment is to invest $100,000 for a client. Because the funds are to be invested in a business at the end of 1 year, you have been instructed to plan for a 1- year holding period. Further, your boss has restricted you to the following investment alternatives in the table below, shown with their probabilities and associated outcomes. (Disregard for now the items at the bottom of the data; you will fill in the blanks later.) Merrill Finch's economic forecasting staff has developed probability estimates for the state of the economy, and its security analysts have developed a sophisticated computer program, which was used to estimate the rate of return on each alternative under each state of the economy. High Tech Inc. is an electronics firm; Collections Inc. collects past-due debts; and U.S. Rubber manufactures tires and various other rubber and plastics products. Merrill Finch also maintains a "market portfolio" that owns a market- weighted fraction of all publicly traded stocks; you can in- vest in that portfolio, and thus obtain average stock market results. Given the situation as described, answer the follow ing questions. a. (1) Why is the T-bill's return independent of the state ( the economy? Do T-bills promise a completely risk-fre return? (2) Why are High Tech's returns expected t move with the economy whereas Collections' are e pected to move counter to the economy? b. Calculate the expected rate of return on each alternativ and fill in the blanks on the row for k in the table belo c. You should recognize that basing a decision solely on e: pected returns is only appropriate for risk-neutral ind viduals. Since your client, like virtually everyone, is ris averse, the riskiness of each alternative is an importa aspect of the decision. One possible measure of risk is th standard deviation of returns. (1) Calculate this value fo each alternative, and fill in the blank on the row for o the table below. (2) What type of risk is measured by th standard deviation? (3) Draw a graph that shows rough the shape of the probability distributions for High Tec U.S. Rubber, and T-bills. d. Suppose you suddenly remembered that the coefficient variation (CV) is generally regarded as being a bett measure of stand-alone risk than the standard deviatic when the alternatives being considered have widely di RETURNS ON ALTERNATIVE INVESTMENTS ESTIMATED RATE OF RETURN PROBABILITY T-BILLS HIGH TECH U.S. MARKET COLLECTIONS RUBBER PORTFOLIO 2-STOCK PORTFOLIO 0.1 8.0% (22.0%) 28.0% 0.2 10.0% (13.0%) 8.0 (2.0) 14.7 (10.0) 0.4 1.0 8.0 20.0 7.0 0.2 15.0 10.0 8.0 35.0 45.0 29.0 0.1 8.0 50.0 30.0 43.0 15.0 13.8% 15.0% 0.0 18.8 15.3 CV 3.3 7.9 1.4 1.0 0.3 b -0.87 0.89 Note that the estimated returns of U.S. Rubber do not always move in the same direction as the overall economy. For example, when the economy is below average, consumers purchase fewer tires than they would if the economy was stronger. However, if the economy is in a flat-out recession, a large number of consumers who were planning to purchase a new car may choose to wait and instead purchase new tires for the car they currently own, Under these circumstances, we would expect U.S. Rubber's stock price to be higher if there is a recession than if the economy was just below average. RETURN() RISK (BETA) fering expected returns. Calculate the missing CVs, and fill in the blanks on the row for CV in the table above. Does the CV produce the same risk rankings as the stan- dard deviation? SECURITY High Tech Market 17.4% 1.30 15.0 1.00 13.8 0.89 U.S. Rubber T-bills 8.0 0.00 Collections 1.7 e. Suppose you created a 2-stock portfolio by investing $50,000 in High Tech and $50,000 in Collections. (1) Calculate the expected return (k), the standard devi- ation (o,), and the coefficient of variation (CV) for this portfolio and fill in the appropriate blanks in the table above. (2) How does the riskiness of this 2-stock portfolio compare with the riskiness of the individual stocks if they were held in isolation? (0.87) f. Suppose an investor starts with a portfolio consisting of one randomly selected stock. What would happen (1) to the riskiness and (2) to the expected return of the port- folio as more and more randomly selected stocks were added to the portfolio? What is the implication for in- vestors? Draw a graph of the two portfolios to illustrate (1) What is a beta coefficient, and how are betas used in risk analysis? (2) Do the expected returns appear to be re- lated to each alternative's market risk? (3) Is it possible to choose among the alternatives on the basis of the infor- mation developed thus far? Use the data given at the start of the problem to construct a graph that shows how the T-bill's, High Tech's, and the market's beta coefficients are calculated. Then discuss what betas measure and how they are used in risk analysis. your answer. i. g. (1) Should portfolio effects impact the way investors think about the riskiness of individual stocks? (2) If you decided to hold a 1-stock portfolio, and consequently were exposed to more risk than diversified investors, could you expect to be compensated for all of your risk that is, could you earn a risk premium on that part of your risk that you could have eliminated by diversifying? h. The expected rates of return and the beta coefficients of the alternatives as supplied by Merrill Finch's computer program are as follows: The yield curve is currently flat, that is, long-term Tres- sury bonds also have an 8 percent yield. Consequently, Merrill Finch assumes that the risk-free rate is 8 percent. (1) Write out the Security Market Line (SML) equation, use it to calculate the required rate of return on each al- ternative, and then graph the relationship between the expected and required rates of return. (2) How do the ex- pected rates of return compare with the required rates of return? (3) Does the fact that Collections has an expected return that is less than the T-bill rate make any sense? STATE OF THE ECONOMY Recession Below average Average Above average Boom k 0.0 (10,0) (20.0) 1.7% 13.4 (4) What would be the market risk and the required re- turn of a 50-50 portfolio of High Tech and Collections? Of High Tech and U.S. Rubber? j. (1) Suppose investors raised their inflation expectations by 3 percentage points over current estimates as reflected in the 8 percent risk-free rate. What effect would higher in- flation have on the SML and on the returns required on high- and low-risk securities? (2) Suppose instead that in- vestors' risk aversion increased enough to cause the market risk premium to increase by 3 percentage points. (Inflation remains constant.) What effect would this have on the SML and on returns of high- and low-risk securities? CYBER PROBLEM Please go to our web site http://brigham.swlearning.com to access the Cyberproblems. THOMSON With your Xtra! CD-ROM, access the Thomson Analytics Problems and use the Thomson Analytics Academic online database to work this chapter's problems. ANALYTICS