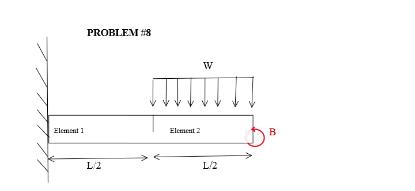
The moment of inertia of the beam is I, elastic modulus is E and the mass of the beam is m. The total length of the beam equals 1. There is a distributed load W (N/m) over element 2 and a moment B (N-m) at the free end a) Draw a diagram of both elements with the loads and moments distributed along the nodes. Draw arrows for the degree of freedom at the nodes. b) Write down the elemental stiffness matrix per element. c) Turn the element stiffness matrix into a global stiffness matrix. d) Show the displacement vector and force vector. Remember to integrate the relevant boundary Conditions/loads. e) Determined the reduced stiffness matrix and reduced force vector. f) Assemble a global mass matrix using the elemental mass matrix below 000 m0 1/12 0 0 0 0 1 0 0 12/12 20 Lo g) Set up to solve for the eigenvalues of the beam. Element 1 PROBLEM #8 L2 ITT Element 2 W L/2 B