Answer the following.

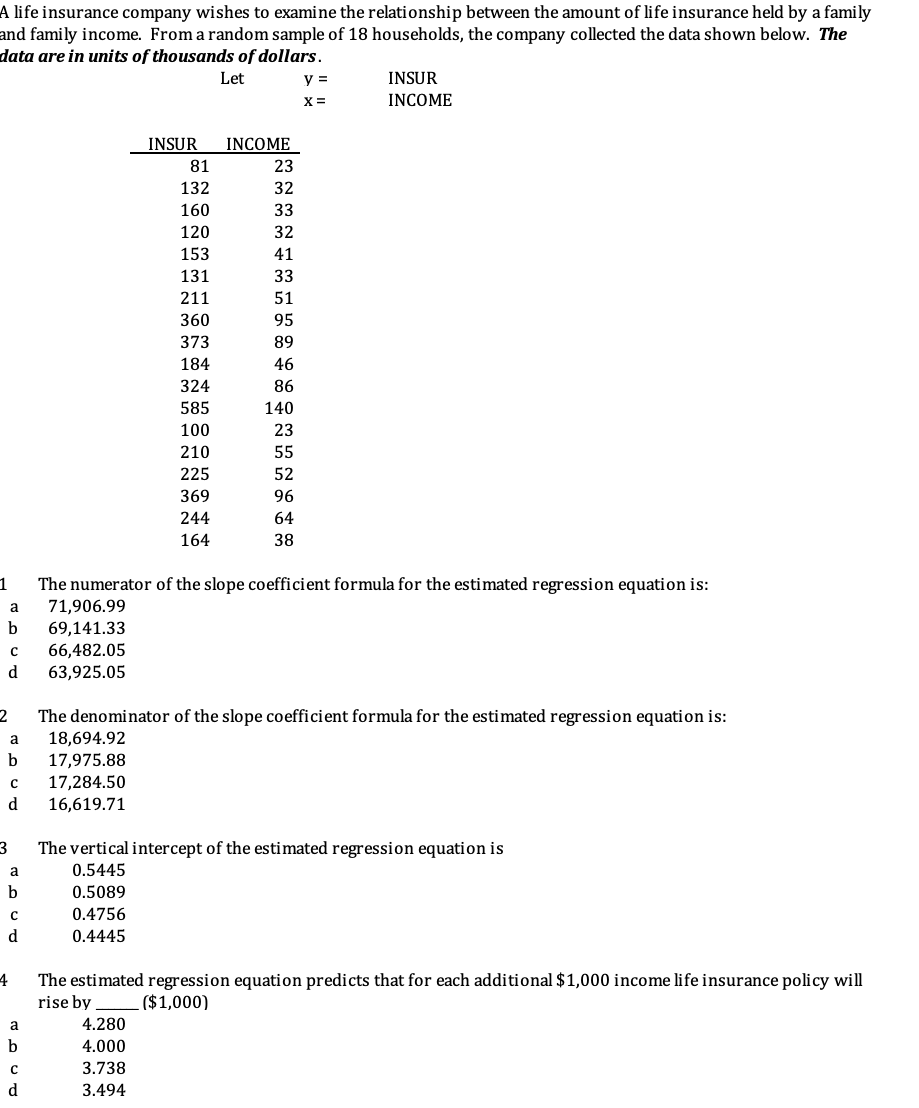
A life insurance company wishes to examine the relationship between the amount of life insurance held by a family and family income. From a random sample of 18 households, the company collected the data shown below. The data are in units of thousands of dollars. Let V= INSUR X = INCOME INSUR INCOME 81 23 132 32 160 33 120 32 153 41 131 33 211 51 360 95 373 89 184 46 324 86 585 140 100 23 210 55 225 52 369 96 244 64 164 38 The numerator of the slope coefficient formula for the estimated regression equation is: 71,906.99 69,141.33 66,482.05 63,925.05 The denominator of the slope coefficient formula for the estimated regression equation is: 18,694.92 17,975.88 17,284.50 16,619.71 The vertical intercept of the estimated regression equation is 0.5445 0.5089 0.4756 0.4445 The estimated regression equation predicts that for each additional $1,000 income life insurance policy will rise by . ($1,000) 4.280 4.000 3.738 3.4945 The income of one policy holder is 55 ($1000). The predicted life insurance policy is_ _ ($1,000) 248.095 238.552 229.377 220.555 The observed policy amount for the policy holder in previous question is 210 ($1,000) The prediction error is -11.860 -11.188 -10.555 -9.958 The sum of squared errors (SSE) is, 4,562.1 4,303.9 4,060.3 3,830.4 8 The sum of squared total (SST) is, 280,409.1 272,241.9 264,312.5 256,614.1 The sum of squared explained deviations (SSR) is, 302,225.0 293,422.3 284,876.0 276,578.7 10 The observed insurance policy deviates from the predicted policy, on average, by ($1,000) 13.964 14.699 15.473 16.287 11 The sample data provides that fraction of variations in the life insurance policy is explained by income. 0.9962 0.9863 0.9370 0.8902 12 For the purpose of statistical inference for the slope parameter, the standard error of the slope coefficient, se(b, ), is 0.118 0.124 0.130 0.13713 The t-score to find the margin of error for a 95% interval estimate of the population slope parameter [31 is, a 1.818 b 1.913 c 2.014- d 2.120 14- The margin of error for a 95% condence interval for the population slope parameter is ($1,000), a 0.225 b 0.237 c 0.249 d 0.263 15 To perform a test of hypothesis that the population slope parameter is zero, the test statistic t is . a 33.99:) b 35.773 c 37.661 d 39.64-4- I .l