Answer the following questions down below

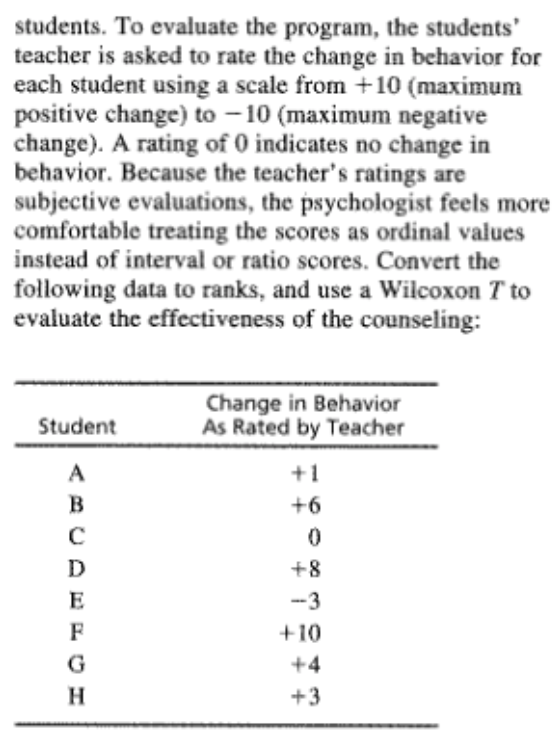
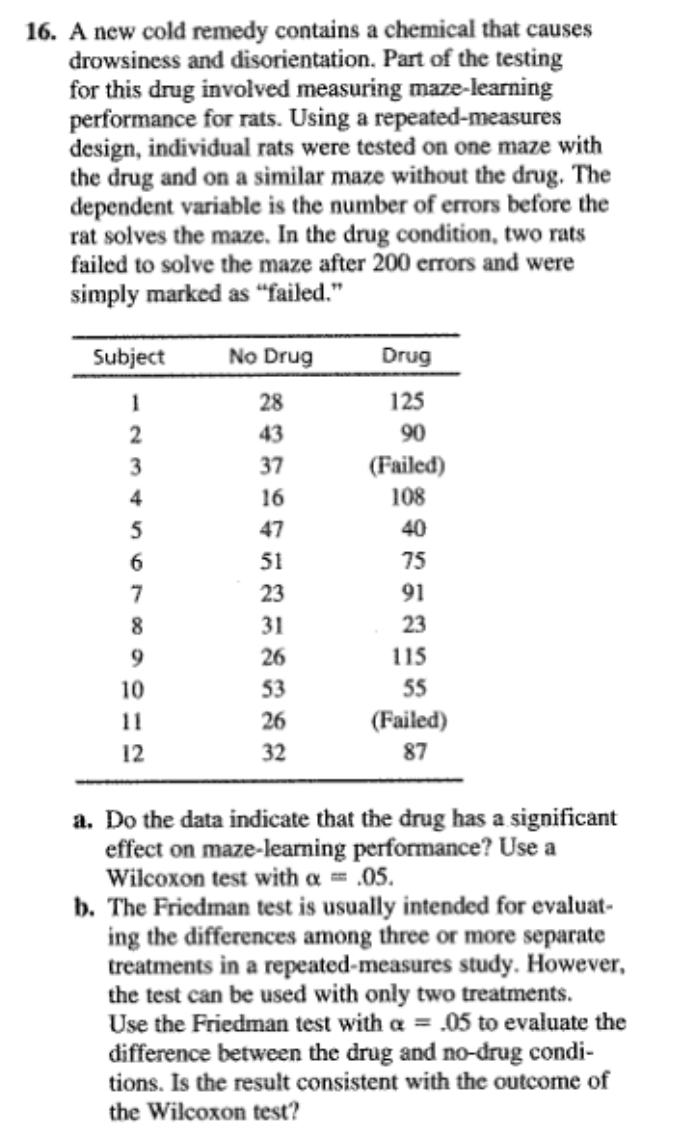
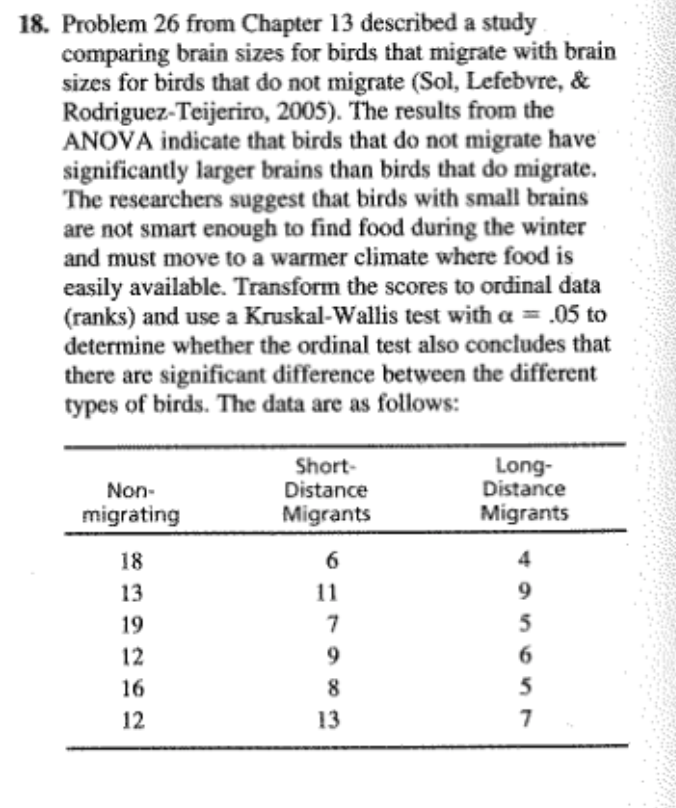
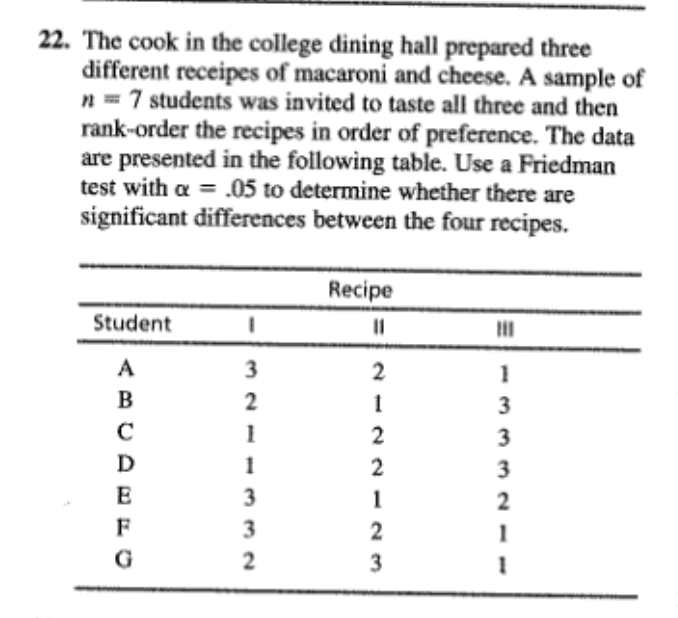
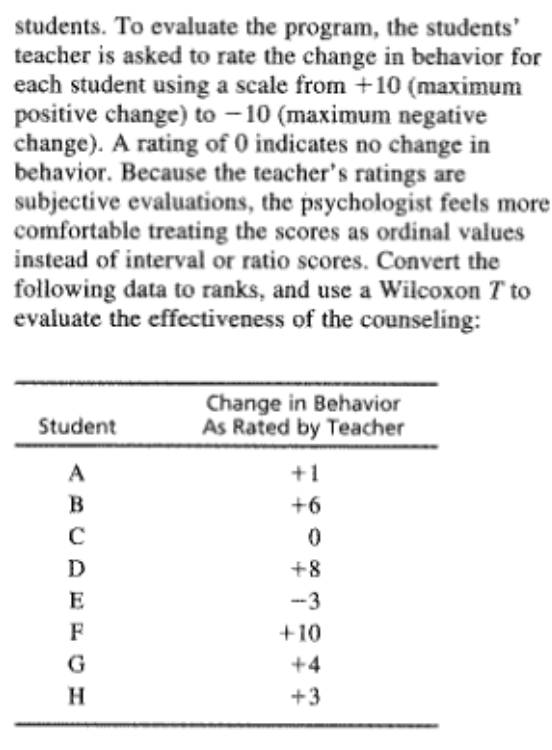
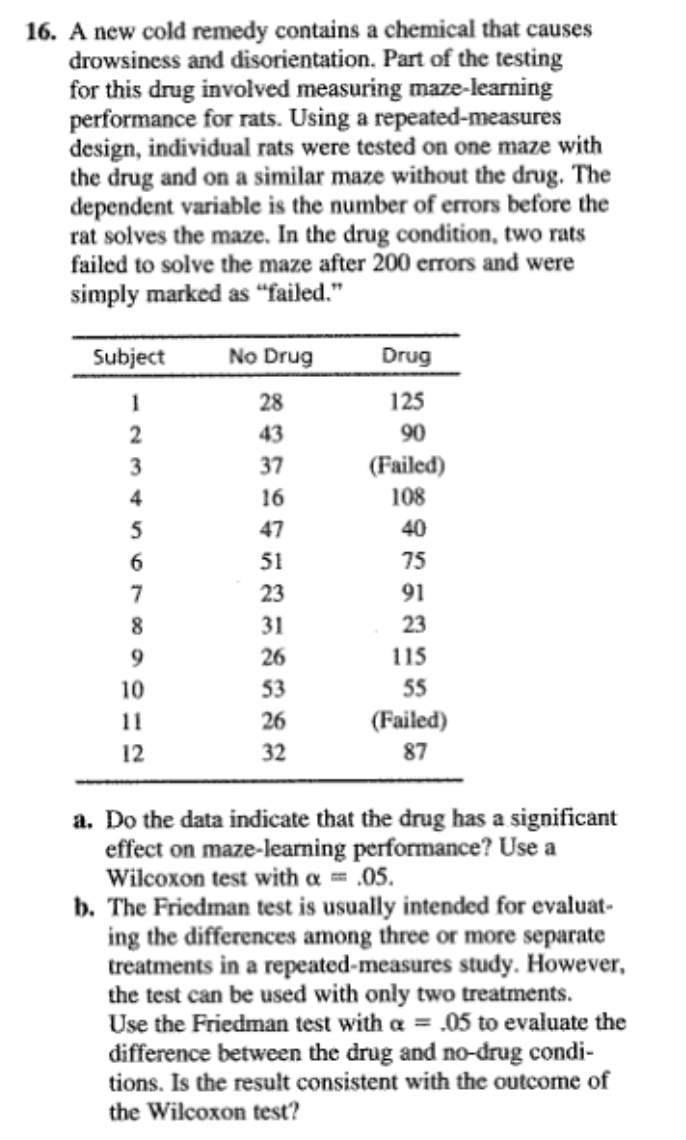
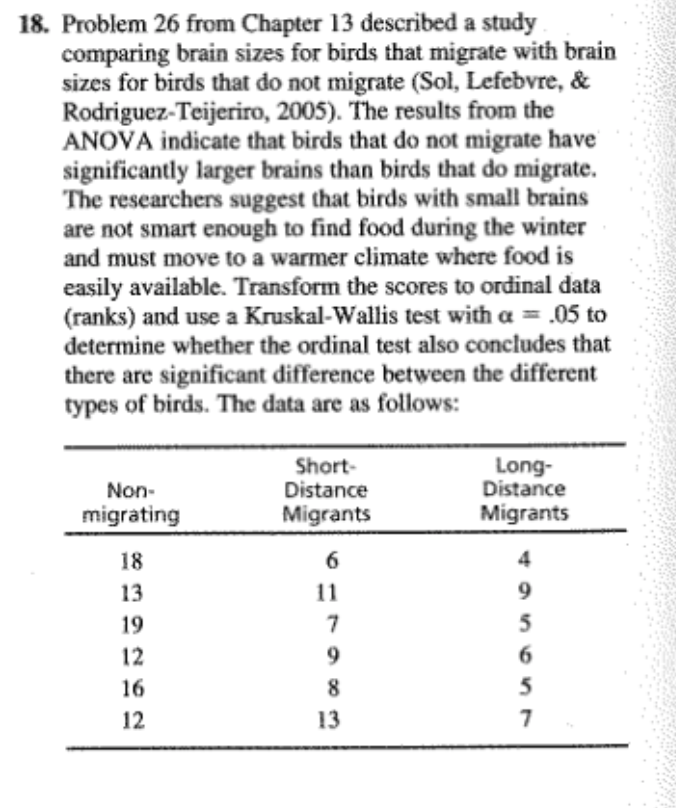
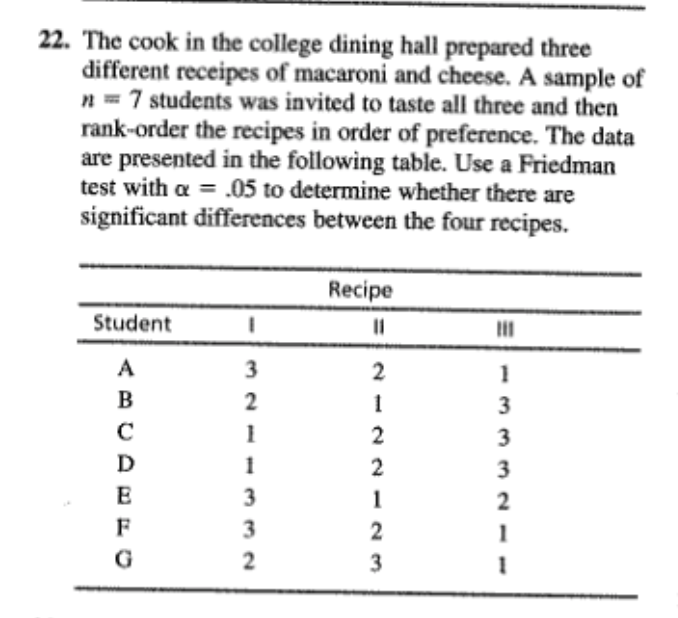
2. Following is a set of numerical scores for a sample of n = 8 subjects. Find the rank for each subject. Subject: A B C D E F G H Score: 12 12 19 19 19 24 27 304. Problem 22 from Chapter 10 described an experiment in which humorous sentences were presented to one group and nonhumorous sentences to another group (Schmidt, 1994). Both groups were then tested to see how many sentences they could recall. The data are as follows: Number of Sentences Recalled Humorous Nonhumorous Sentences Sentences 5 2 4 5 2 N 6 7 6 6 2 1 2 5 4 3 3 2 3 3 3 5 w 4 The independent-measures ? test showed a significant difference between the two types of sentences. Transform the scores to ordinal data (ranks) and use a Mann-Whitney test with a = .05 to determine whether the ordinal test produces the same conclusion.6. One of the advantages of using ranks (ordinal data) instead of interval or ratio scores is that ranks can reduce the effect of one extreme individual score. The following data represent results from an independent- measures study comparing two treatments. Notice that most subjects in treatment 1 have scores around 40, and most subjects in treatment 2 have scores around 15. However, there is one odd individual in treatment 2 with a score of X = 104. This extreme score distorts the data so that an independent-measures / test indicates no significant difference between treatments, *(10) = 0.868, p > .05. When the scores are converted to ranks, however, the effect of the extreme score is much less dramatic. Transform the score into ranks and use a Mann-Whitney test to evaluate the difference between treatments. Test with a = .05. Treatment 1 Treatment 2 22 16 39 10 37 14 16 17 12 57 104 M = 39.00 M = 27.00 s = 11.30 S = 34.048. One assumption for parametric tests with independent- measures data is that the different treatment conditions have the same variance (homogeneity-of-variance assumption). However, a treatment effect that increases the mean often also increases the variability. In this situation, the parametric f test or ANOVA is not justified, and a Mann-Whitney test should be used. The following data represent an example of this situation: Treatment 1 Treatment 2 (Sample A) (Sample B) 20 14 WNANDU- 27 6 10 19 a. Compute the mean and variance for each sample. Note the difference between the two sample variances. b. Use a Mann-Whitney test, with a = .05, to test for a significant difference between the two treatments.10. Problem 22 from Chapter 11 described a research study comparing the accuracy of Olympic marksmen for shots fired during a heartbeat with the accuracy for shots fired between heartbeats (Pelton, 1983). The repeated-measures : test showed a significant difference between the two conditions. Transform the scores to ordinal data (ranks) and use a Wilcoxon test with a = .05 to determine whether the ordinal test produces the same conclusion. The data are as follows: During Between Participant Heartbeats Heartbeats 9312. In a repeated-measures research study comparing two treatments, if all of the subjects show a decrease in scores for treatment 2 compared with treatment 1, then what is the minimum number of subjects needed to demonstrate a significant difference between treatments at the .05 level of significance?14. The school psychologist at an elementary school is conducting a counseling program for disruptivestudents. To evaluate the program, the students' teacher is asked to rate the change in behavior for each student using a scale from + 10 (maximum positive change) to - 10 (maximum negative change). A rating of 0 indicates no change in behavior. Because the teacher's ratings are subjective evaluations, the psychologist feels more comfortable treating the scores as ordinal values instead of interval or ratio scores. Convert the following data to ranks, and use a Wilcoxon T to evaluate the effectiveness of the counseling: Change in Behavior Student As Rated by Teacher +1 +6 +316. A new cold remedy contains a chemical that causes drowsiness and disorientation. Part of the testing for this drug involved measuring maze-learning performance for rats. Using a repeated-measures design, individual rats were tested on one maze with the drug and on a similar maze without the drug. The dependent variable is the number of errors before the rat solves the maze. In the drug condition, two rats failed to solve the maze after 200 errors and were simply marked as "failed." Subject No Drug Drug 28 125 43 90 37 (Failed) 16 108 47 40 51 75 91 23 115 53 55 26 (Failed) 32 87 a. Do the data indicate that the drug has a significant effect on maze-learning performance? Use a Wilcoxon test with o = .05. b. The Friedman test is usually intended for evaluat ing the differences among three or more separate treatments in a repeated-measures study. However, the test can be used with only two treatments. Use the Friedman test with a = .05 to evaluate the difference between the drug and no-drug condi- tions. Is the result consistent with the outcome of the Wilcoxon test?18. Problem 26 from Chapter 13 described a study comparing brain sizes for birds that migrate with brain sizes for birds that do not migrate (Sol, Lefebvre, & Rodriguez-Teijeriro, 2005). The results from the ANOVA indicate that birds that do not migrate have significantly larger brains than birds that do migrate. The researchers suggest that birds with small brains are not smart enough to find food during the winter and must move to a warmer climate where food is easily available. Transform the scores to ordinal data (ranks) and use a Kruskal-Wallis test with a = .05 to determine whether the ordinal test also concludes that there are significant difference between the different types of birds. The data are as follows: Short- Long- Non- Distance Distance migrating Migrants Migrants 18 13 19 12 16 1220. A researcher who is interested in the relationship between health and personality obtains a sample of n = 25 men between the ages of 30 and 35. The men are all given a physical exam by a doctor who then rank-orders the men in terms of overall health. The men are also given personality tests that classify them as either alpha, beta, or gamma personality types. Alphas are cautious and steady, betas are carefree and outgoing, and gammas tend toward extremes of behavior. The health rankings for the three groups of participants are as follows: Alphas: 2nd, 6th, 7th, 10th, 13th, 15th, 19th, 21st, 23rd Betas: 1st, 3rd, 5th, 8th, 11th, 12th, 16th, 17th Gammas: 4th, 9th, 14th, 18th, 20th, 22nd, 24th, 25th Do these data indicate significant differences in health among the three personality types? Test at the .01 level of significance.22. The cook in the college dining hall prepared three different receipts of macaroni and cheese. A sample of " = 7 students was invited to taste all three and then rank-order the recipes in order of preference. The data are presented in the following table. Use a Friedman test with a = .05 to determine whether there are significant differences between the four recipes. Recipe Student 11 A WNENNEN - -NWWW- NWWHENW24. In Chapter 14 we noted that one advantage of transform the scores to ordinal data (ranks) and repeated-measures studies compared to independent- use a Friedman test with a = .05 to evaluate the measures is that the repeated-measures studies reduce differences between treatments. the variance by removing individual differences. c. Do the ordinal tests show the same pattern as the With smaller variance, the ANOVA is more likely to I tests? That is, is there a significant difference for produce a significant effect. The following data were the repeated-measures design but no significant used in problem 14 from Chapter 14 to demonstrate difference for the independent-measures data? this advantage. If the data are treated as three separate samples, the independent-measures ANOVA shows Treatments no significant difference. However, if the data are treated as the same sample in three treatments, the A B C repeated-measures ANOVA shows significant differences between the treatments. a. Treat the scores as three separate samples, NU-NO transform the scores to ordinal data (ranks), then use a Kruskal-Wallis test with a = .05 to evaluate the differences between treatments. b. Treat the data as a repeated-measures study with the same sample in all three treatments, then