Answers needed

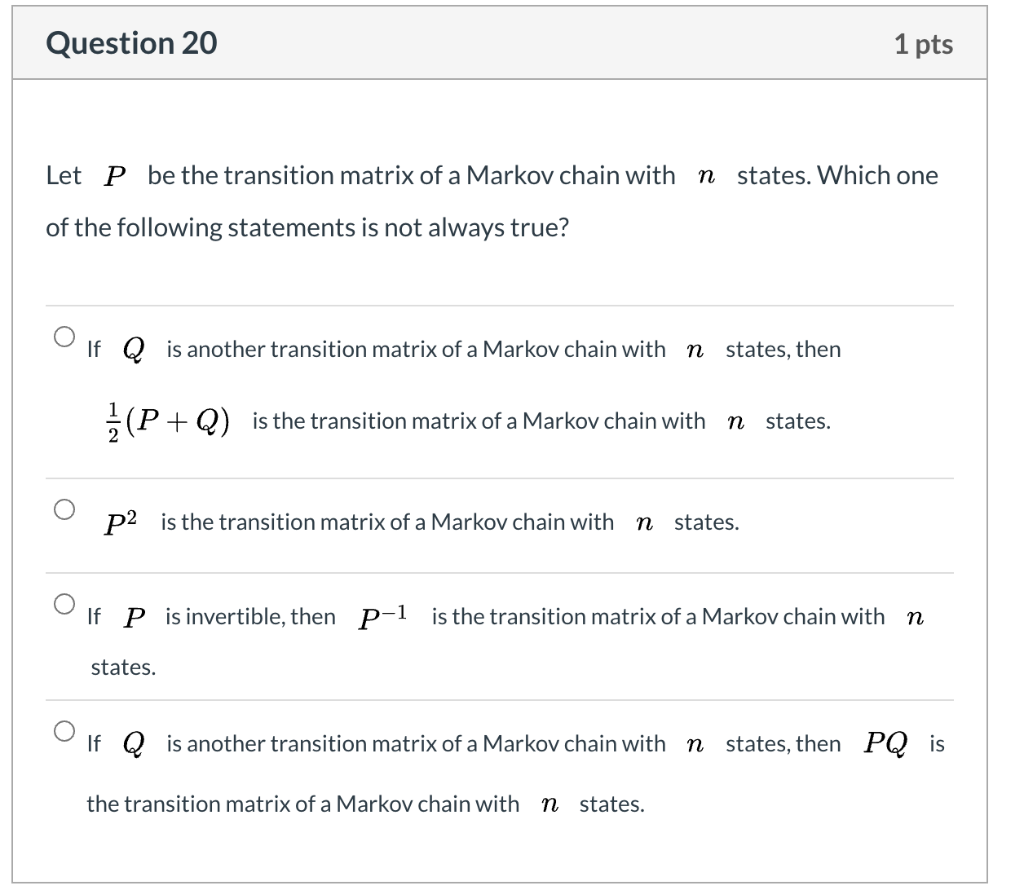
2. A Markov chain with state space {1, 2, 3} has transition probability matrix 00 0.3 0.1 a: 0.3 0.3 0.4 0.4 0.1 0.5 (a) Is this Markov chain irreducible? Is the Markov chain recurrent or transient? Explain your answers. (b) What is the period of state 1? Hence deduce the period of the remaining states. Does this Markov chain have a limiting distribution? (c) Consider a general three-state Markov chain with transition matrix 3011 3012 1013 P = P21 P22 P23 1031 P32 P33 Give an example of a specic set of probabilities jag-'3; for which the Markov chain is not irreducible (there is no single right answer to this1 of course l]. Question 20 1 pts Let P be the transition matrix of a Markov chain with n states. Which one of the following statements is not always true? If Q is another transition matrix of a Markov chain with n states, then =(P + Q) is the transition matrix of a Markov chain with n states. O P2 is the transition matrix of a Markov chain with n states. If P is invertible, then p-1 is the transition matrix of a Markov chain with n states. If Q is another transition matrix of a Markov chain with n states, then PQ is the transition matrix of a Markov chain with n states.4. Consider the Markov chain X" = {X,} with state space S = {0, 1, 2, ...} and transition probabilities 1 ifj=i-1 Puj = 10 otherwise , for i 2 1 and Poo = 0, Poj = for j > 1. (a) Is this Markov chain irreducible? Determine the period for every state. (b) Is the Markov chain recurrent or transient? Explain. (c) Is the Markov chain positive recurrent? If so, compute the sta- tionary probability distribution. (d) For each state i, what is the expected number of steps to return to state i if the Markov chain X starts at state i? 5. Consider a Markov chain X = {X} with state space S = {0, 1, 2, ...} and transition probability matrix 0 1 0 0 P 0 0 P = O p 0 q 0 0 . . . 0 0 P 0 4 0 Here p > 0, q > 0 and p+q =1. Determine when the chain is positive recurrent and compute its stationary distribution.2. Recall that Markov's inequality says that if T' is a positive-valued random variable with mean E(T) then E(T) P(T > 1 ) 0 there holds P(1X - #| Ska) 21 - 1 That is. with probability at least 1 - 2. X stays within & standard deviations around its mean