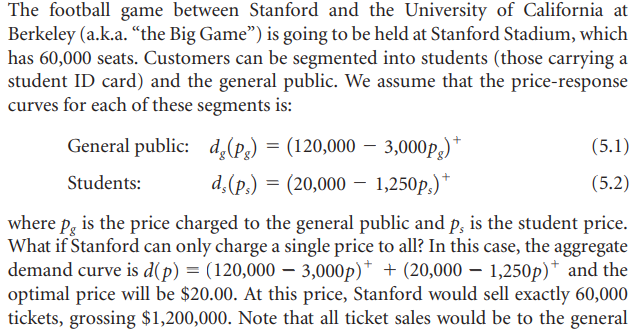
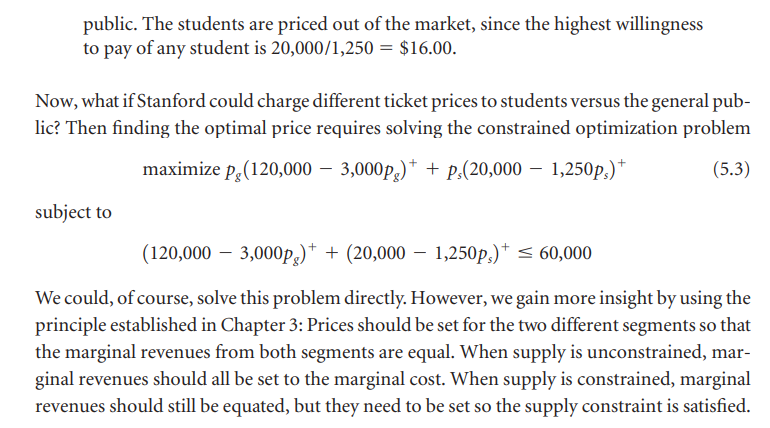
a.Optimal prices with 10% buy down

b. Total revenue vs the base case without cannibalization

c. How much the university would be willing to pay for the photo ID cards?

How do the optimal prices for the student and general public, and the total revenue change as the buy down percentage () changes from zero to 100%? Solve the problem for 10% increments of .

Textbook pricing and revenue optimization robert l. phillips.... pdf is free

The football game between Stanford and the University of California at Berkeley (a.k.a. the Big Game) is going to be held at Stanford Stadium, which has 60,000 seats. Customers can be segmented into students (those carrying a student ID card) and the general public. We assume that the price-response curves for each of these segments is: General public: dg(P) = = (120,000 3,000pg)* (5.1) Students: d:(ps) = (20,000 1,250p)* (5.2) where pg is the price charged to the general public and ps is the student price. What if Stanford can only charge a single price to all? In this case, the aggregate demand curve is d(p) = (120,000 3,000p)* + (20,000 1,250p) and the optimal price will be $20.00. At this price, Stanford would sell exactly 60,000 tickets, grossing $1,200,000. Note that all ticket sales would be to the general public. The students are priced out of the market, since the highest willingness to pay of any student is 20,000/1,250 = $16.00. Now, what if Stanford could charge different ticket prices to students versus the general pub- lic? Then finding the optimal price requires solving the constrained optimization problem maximize pg(120,000 3,000pg)* + P (20,000 1,250ps)* (5.3) subject to (120,000 3,000pc)+ + (20,000 1,250ps)+ = 60,000 We could, of course, solve this problem directly. However, we gain more insight by using the principle established in Chapter 3: Prices should be set for the two different segments so that the marginal revenues from both segments are equal. When supply is unconstrained, mar- ginal revenues should all be set to the marginal cost. When supply is constrained, marginal revenues should still be equated, but they need to be set so the supply constraint is satisfied. We return to the Stanford Stadium pricing problem in Section 5.4, assuming a capacity of 60,000 seats and the demand curves for students and for the general public as given in Equations 5.1 and 5.2. Assume that 5% of the general public will masquerade as students (perhaps using borrowed ID cards) in order to save money. Assuming that Stanford knows that, what are the optimal prices for student tickets and general public tickets it should set in this case? What is the total revenue, and how does it compare to the case without cannibalization? What does this say about the amount that Stanford would be willing to pay for such devices as photo ID cards in order to eliminate cannibalization? The football game between Stanford and the University of California at Berkeley (a.k.a. the Big Game) is going to be held at Stanford Stadium, which has 60,000 seats. Customers can be segmented into students (those carrying a student ID card) and the general public. We assume that the price-response curves for each of these segments is: General public: dg(P) = = (120,000 3,000pg)* (5.1) Students: d:(ps) = (20,000 1,250p)* (5.2) where pg is the price charged to the general public and ps is the student price. What if Stanford can only charge a single price to all? In this case, the aggregate demand curve is d(p) = (120,000 3,000p)* + (20,000 1,250p) and the optimal price will be $20.00. At this price, Stanford would sell exactly 60,000 tickets, grossing $1,200,000. Note that all ticket sales would be to the general public. The students are priced out of the market, since the highest willingness to pay of any student is 20,000/1,250 = $16.00. Now, what if Stanford could charge different ticket prices to students versus the general pub- lic? Then finding the optimal price requires solving the constrained optimization problem maximize pg(120,000 3,000pg)* + P (20,000 1,250ps)* (5.3) subject to (120,000 3,000pc)+ + (20,000 1,250ps)+ = 60,000 We could, of course, solve this problem directly. However, we gain more insight by using the principle established in Chapter 3: Prices should be set for the two different segments so that the marginal revenues from both segments are equal. When supply is unconstrained, mar- ginal revenues should all be set to the marginal cost. When supply is constrained, marginal revenues should still be equated, but they need to be set so the supply constraint is satisfied. We return to the Stanford Stadium pricing problem in Section 5.4, assuming a capacity of 60,000 seats and the demand curves for students and for the general public as given in Equations 5.1 and 5.2. Assume that 5% of the general public will masquerade as students (perhaps using borrowed ID cards) in order to save money. Assuming that Stanford knows that, what are the optimal prices for student tickets and general public tickets it should set in this case? What is the total revenue, and how does it compare to the case without cannibalization? What does this say about the amount that Stanford would be willing to pay for such devices as photo ID cards in order to eliminate cannibalization