Approximations

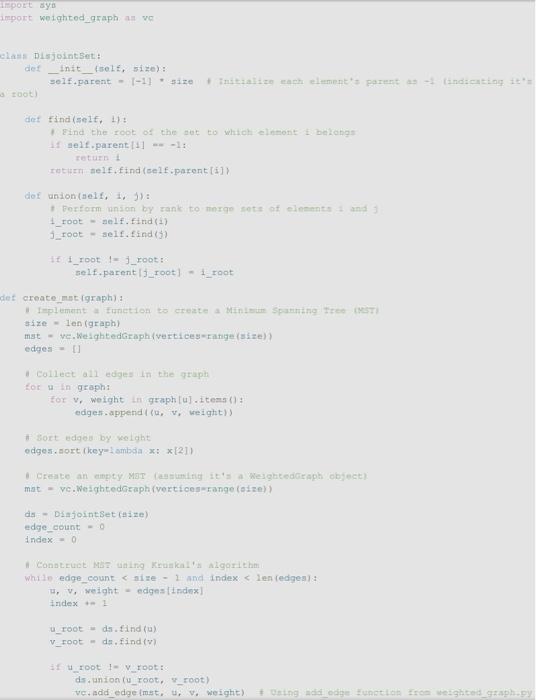
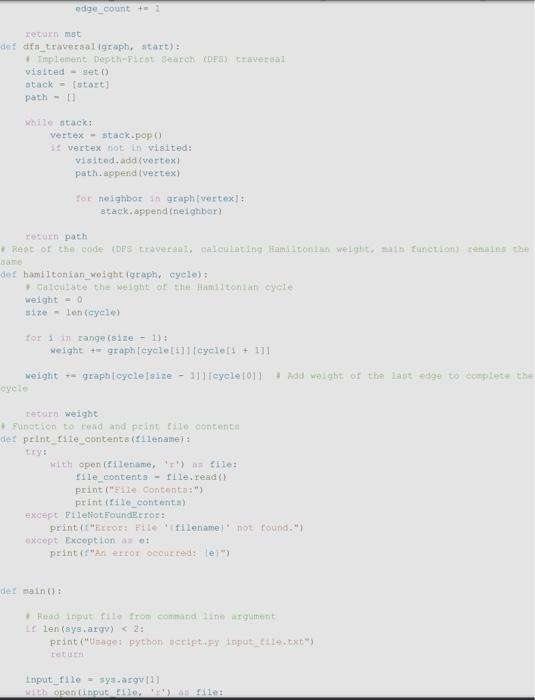
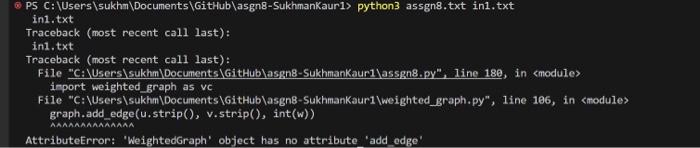
need to construct mst(kruskal way), disjoint set class utilizing nested edge list, once tree is constucted going to do dfs sorting by previsit number and then give hamiltonian cycle and weight. I have coded stuff but its not working, my errors are attached. I want to send input file to the weighted graph class which is provided and use that to do the requirements. PLEASE HELP and answer all question(dont just chatgpt please). i will give thumbs up if you actually help me!!

Lab prompt

my code:

provide weight_graph.py

my errors

There are numerous problems in computer science that simply cannot be solved efficiently, assuming 1 that P=NP. Since those problems often have real-world applications, it is worthwhile to consider approximating their solutions, effectively trading some amount of correctness for complexity. Part 1: The Traveling Salesperson Problem The Traveling Salesperson Problem, or "TSP", asks for the Hamiltonian cycle of minimum weight in a complete, weighted graph. It is one of the most famously difficult problems in computer science and graph theory 2. In order to make approximation feasible, we restrict the problem to its metric case: all edge weights must satisfy the triangle inequality. For example: In the above complete, weighted graph, the Hamiltonian cycle of minimum weight is (v0,v1,v3,v2,v4,v0). Part 2: Approximating Metric TSP Once restricted to the metric case, there exists a polynomial time approximation algorithm. Note that removing an edge from a Hamiltonian cycle must yield a spanning tree. An MST thus represents a somewhat similar structure to a solution to TSP - but one that is much easier to find. These observations inform a 2-approximation, as follows: 1. Construct an MST, which can be done greedily and requires linearithmic time. In the graph above, there is only one such tree, containing the edges {(v0,v1),(v2,v3),(v2,v4),(v1,v3)} : IAnd it certainly appenrs to be a safe assumption. 2 Not only is TSP itself NP-Hard, but meroly approximating the getueral case of TSP' is also NP-Hard. 2. Certainly, a tree is not a cycle. Explore this tree in depth-first fashion, effectively traversing each edge twice, which requires linear time. From above 3, we have (v0,v1,v3,v2,v3,v1,v4,v1,v0) : 3. This cycle is neither Hamiltonian nor valid in the given graph. Bypass any previously explored vertices 4, which requires linear time. In this case, this gives (v0,v1,v3,v2,v4,v0) : In your programming language of choice (see Assignment 1), implement this polynomial time 2-approximation for the metric case of the Traveling Salesperson Problem. Each input graph will be provided as an edge list: each edge in the graph will be represented by a commaseparated triple consisting of two vertex identifiers and a weight, indicating an edge between the first vertex and the second of that weight. You may assume that vertex identifiers are contiguous natural numbers they begin at 0 , and there will be no "gaps" in the identifiers used. You may further assume that the graph will be complete, with at least 3 vertices and natural weights satisfying the triangle inequality. For example, the above graph could be represented as: 0,1,20,2,70,3,60,4,41.2,61.3,51,4,32,3,22,4,83,4,7 Your program must accept as a command line argument the name of a file containing an edge list as described above, then print to stdout a Hamiltonian cycle of approximately minimum weight, along with that weight. For example: >$./ compile.sh >$./ run.sh in1.txt Hamiltonian cycle of weight 21: 0,1,3,2,4,0 3 Ascaming ties are broken in ascending sumerical order. 4With the exaption of the first vertex, which must, by convention, appear a second time as the last vertex. Inpoet syo import weighted_graph an vo clais Disjointset: det _init_folt, size): soot) det findiself, 1): 1. Eind the root of the sut to which elentont i betobigs if delf.pareat [1] =1 : return i ratirra melf, find (self,parent [i]) dot union(telf, 1, j): 1.root - aelf. find (i) j_root - self.find (j) 16. 1_root 1=3 root: self.parent [3_root] - 1_root det create met (graph): 1 Inplement a fanction to create a Minimin spaming free (KST) aize - len (graph) mist - ve.WeightedGraphivertices-tange (stize) edges: =[1] Collect all edges in the graph for a in graph: edges.append ( u, v, weight)) B Sort edges by welght edges. sort (key=1 smbda x: : [2] ) mat = vc.WeightedGraph(verticesurange (oize)) ds - - DiajointBet (+ize) edge_count =0 index =0 White edge_count $./ compile.sh >$./ run.sh in1.txt Hamiltonian cycle of weight 21: 0,1,3,2,4,0 3 Ascaming ties are broken in ascending sumerical order. 4With the exaption of the first vertex, which must, by convention, appear a second time as the last vertex. Inpoet syo import weighted_graph an vo clais Disjointset: det _init_folt, size): soot) det findiself, 1): 1. Eind the root of the sut to which elentont i betobigs if delf.pareat [1] =1 : return i ratirra melf, find (self,parent [i]) dot union(telf, 1, j): 1.root - aelf. find (i) j_root - self.find (j) 16. 1_root 1=3 root: self.parent [3_root] - 1_root det create met (graph): 1 Inplement a fanction to create a Minimin spaming free (KST) aize - len (graph) mist - ve.WeightedGraphivertices-tange (stize) edges: =[1] Collect all edges in the graph for a in graph: edges.append ( u, v, weight)) B Sort edges by welght edges. sort (key=1 smbda x: : [2] ) mat = vc.WeightedGraph(verticesurange (oize)) ds - - DiajointBet (+ize) edge_count =0 index =0 White edge_count