Question: n Maclaurin Series expansion of the arctangent function x is defined for |x| 1 as (-1) 2n +1 arctan2= Start with the simplest version, arctan

$Maclaurin Series expansion of the arctangent function ( x ) is defined for ( |x| leq 1 ) as [ arctan x=sum_{n=0}^{in$ n

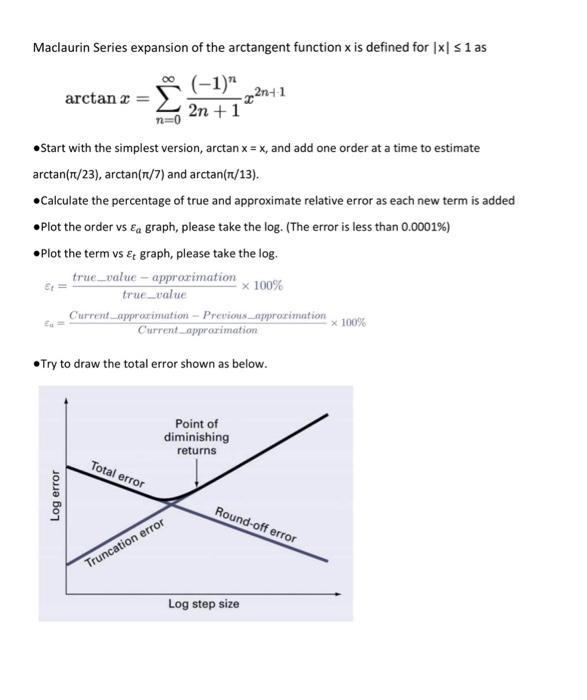
Maclaurin Series expansion of the arctangent function x is defined for |x| 1 as (-1)" 2n +1 arctan2= Start with the simplest version, arctan x = x, and add one order at a time to estimate arctan(r/23), arctan(r/7) and arctan(7/13). Calculate the percentage of true and approximate relative error as each new term is added Plot the order vs Ea graph, please take the log. (The error is less than 0.0001%) Plot the term vs & graph, please take the log. true_value-approximation x 100% true_value Log error Current approximation - Previous approximation Current approximation Try to draw the total error shown as below. -x2n+-1 Total error Point of diminishing returns Truncation error Round-off error Log step size x 100%

Step by Step Solution

★★★★★

3.51 Rating (151 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Databases Questions!

The Maclaurin series expansion for the arctangent of x is defined for ( x ( ¤ 1 as

The Maclaurin series expansion for cos x is Starting with the simplest version, cos x = 1, add terms one at a time to estimate cos (?/3). After each new term is added, compute the-true and...

Planning is one of the most important management functions in any business. A front office managers first step in planning should involve determine the departments goals. Planning also includes...

Use Newtons method with initial approximation x1 = 1 to find x2, the second approximation to the root of the equation x4 x 1 = 0. Explain how the method works by first graphing the function and its...

Consider the first-order SDM model shown in figure(a) Show that the quantization noise power in the signal hand {-B, B} is given by:(b) Using a two-term Taylor series expansion of the sine function...

Evaluate e-5 using two approaches And And compare with the true value of 6.737947 x 10 -3 .Use 20 terms to evaluate each series and compute true and approximate relative errors as terms are added. =...

The following infinite series can be used to approximate e x? : (a) Prove that this Maclaurin series expansion is a special case of the Taylor series expansion [(Eq. (4.7)] with x i? = 0 and h = x...

Use zero-through fourth-order Taylor series expansion to predict (2.5) for (x) = In x using a base point at x = 1. Compute the true percent relative error t for each approximation. Discuss the...

Johnson Industries is considering an expansion project. The necessary equipment could be purchased for $9 million, and the project would also require an initial $3 million investment in net operating...

Use zero- through third-order Taylor series expansions to predict (3) for f (x) = 25x 3 6x 2 + 7x 88 Using a base point at x = 1. Compute the true percent relative error t for each approximation.

bluebird design,inc. is a website design and consulting firm. the firm ues a job order costing system in which each client is a different job. blueboard designassigns direct labor, licensing...

Continue Mini Case 1 (the Accounting Cycle Part 1), the following information is available for FastForward in September that may need adjustments.[1] By the end of September, FastForward has provided...

question 1 A nurse's aide alleged that on August 22, 2012, she was attacked while cleaning a resident's room by a male coworker who attempted to rape her. She was able to escape and reported the...

Karri's manager suspects that the batteries being produced lately don't have enough voltage. the null hypothesis at 5% For a left-tailed test, the critical value of z so that a hypothesis test would...

QUESTION 1 The valuation model that computes the current value of a stock by dividing next year's dividend by the net of the discount rate minus the dividend's growth rate is called the...

Should the packaging be postponed to DC? Penang Electronics (PE) is a contract manufacturer that produces and packages private label products for several retail chains including Target, Best Buy,...

Set the Static IP Address, PrefixLength, and Default Gateway # IP: 1 9 2 . 1 6 8 . 2 1 9 . X ( Determine the last part of thte IP address by adding 2 0 to your seat number: If not in the classroom,...

What is the purpose of the journal wizard?

Indexing can clearly be very beneficial. Why should you not create an index for every column of every table of your database?

Match the following terms and definitions. _________ Composite attribute _________ Associative entity _________ Unary relationship _________ Weak entity _________ Attribute _________ Entity _________...

Fitchwood management would like to use the data mart for drill-down online reporting. For example, a sales manager might want to view a report of total sales for an agent by month and then drill down...

A $6500 loan at 11.25% compounded monthly is to be repaid by three equal payments due 3, 6, and 12 months after the date of the loan. Calculate the size of each payment.

Donnelly Excavating has received two offers on a used backhoe that Donnelly is advertising for sale. Offer 1 is for $10,000 down, $15,000 in 6 months, and $15,000 in 18 months. Offer is for $8000...

Maynard Appliances is holding a Fifty- Fifty Sale. Major appliances may be purchased for nothing down and no interest to pay if the customer pays 50% of the purchase price in six months and the...