Arena simulation question
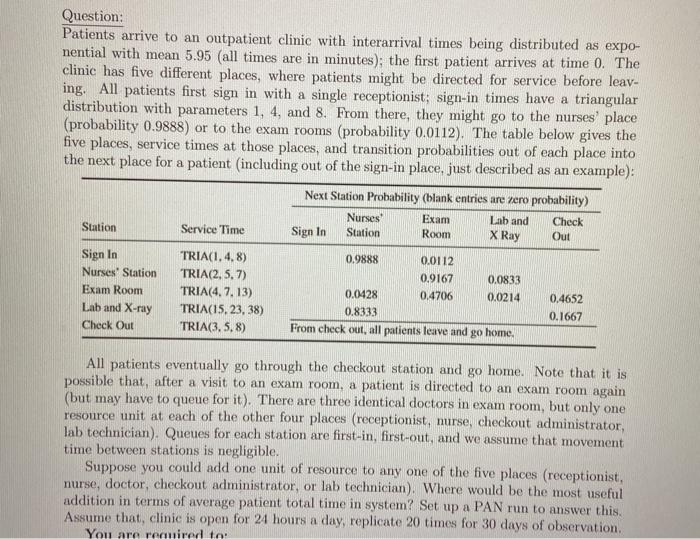
Question: Patients arrive to an outpatient clinic with interarrival times being distributed as expo- nential with mean 5.95 (all times are in minutes); the first patient arrives at time 0. The clinic has five different places, where patients might be directed for service before leav- ing. All patients first sign in with a single receptionist; sign-in times have a triangular distribution with parameters 1, 4, and 8. From there, they might go to the nurses' place (probability 0.9888) or to the exam rooms (probability 0.0112). The table below gives the five places, service times at those places, and transition probabilities out of each place into the next place for a patient (including out of the sign-in place, just described as an example): Next Station Probability (blank entries are zero probability) Nurses Exam Lab and Station Service Time Room X Ray Sign In Station Check Out Sign In Nurses' Station Exam Room Lab and X-ray Check Out TRIAI, 4,8) TRIA(2,5,7) TRIA(4.7.13) TRIA(15, 23, 38) TRIA(3,5,8) 0.9888 0.0112 0.9167 0.0833 0.0428 0.4706 0.0214 0.8333 From check out, all patients leave and go home. 0.4652 0.1667 All patients eventually go through the checkout station and go home. Note that it is possible that, after a visit to an exam room, a patient is directed to an exam room again (but may have to queue for it). There are three identical doctors in exam room, but only one resource unit at each of the other four places (receptionist, nurse, checkout administrator, lab technician). Queues for each station are first-in, first-out, and we assume that movement time between stations is negligible. Suppose you could add one unit of resource to any one of the five places (receptionist, nurse, doctor, checkout administrator, or lab technician). Where would be the most useful addition in terms of average patient total time in system? Set up a PAN run to answer this Assume that, clinic is open for 24 hours a day, replicate 20 times for 30 days of observation. You are required to: Question: Patients arrive to an outpatient clinic with interarrival times being distributed as expo- nential with mean 5.95 (all times are in minutes); the first patient arrives at time 0. The clinic has five different places, where patients might be directed for service before leav- ing. All patients first sign in with a single receptionist; sign-in times have a triangular distribution with parameters 1, 4, and 8. From there, they might go to the nurses' place (probability 0.9888) or to the exam rooms (probability 0.0112). The table below gives the five places, service times at those places, and transition probabilities out of each place into the next place for a patient (including out of the sign-in place, just described as an example): Next Station Probability (blank entries are zero probability) Nurses Exam Lab and Station Service Time Room X Ray Sign In Station Check Out Sign In Nurses' Station Exam Room Lab and X-ray Check Out TRIAI, 4,8) TRIA(2,5,7) TRIA(4.7.13) TRIA(15, 23, 38) TRIA(3,5,8) 0.9888 0.0112 0.9167 0.0833 0.0428 0.4706 0.0214 0.8333 From check out, all patients leave and go home. 0.4652 0.1667 All patients eventually go through the checkout station and go home. Note that it is possible that, after a visit to an exam room, a patient is directed to an exam room again (but may have to queue for it). There are three identical doctors in exam room, but only one resource unit at each of the other four places (receptionist, nurse, checkout administrator, lab technician). Queues for each station are first-in, first-out, and we assume that movement time between stations is negligible. Suppose you could add one unit of resource to any one of the five places (receptionist, nurse, doctor, checkout administrator, or lab technician). Where would be the most useful addition in terms of average patient total time in system? Set up a PAN run to answer this Assume that, clinic is open for 24 hours a day, replicate 20 times for 30 days of observation. You are required to








