As a lab exercise 23.5 A Do-It-Yourself BST, fill in the blanks in the removeRoot method in JM\Ch23\BST\MyTreeSet.java. For extra credit, make MyTreeSet Iterable by implementing an iterator method and a MyTreeSetIterator class. See Section for an example. Your iterator should perform inorder traversal of the tree: left subtree, root, right subtree. Use a Stack in your MyTreeSetIterator class. Do not implement the remove method for your iterator.

Please refer the screenshot images from 1 to 6.jpg

MyTreeSet.java

import java.util.Stack; import java.util.Iterator; import java.util.NoSuchElementException;

/** Implements a BST with TreeNode nodes.

@author TODO Your Name @version TODO Date

@author Period - TODO Your Period @author Assignment - TODO Assignment Name

@author Sources - TODO list collaborators */ public class MyTreeSet implements Iterable { private TreeNode root; // holds the root of this BST

// Constructor: creates an empty BST. public MyTreeSet() { root = null; }

// Returns true if this BST contains value; otherwise returns false. public boolean contains( E value ) { return contains( root, value ); }

// Adds value to this BST, unless this tree already holds value. // Returns true if value has been added; otherwise returns false. public boolean add( E value ) { if ( contains( value ) ) return false; root = add( root, value ); return true; }

// Removes value from this BST. Returns true if value has been // found and removed; otherwise returns false. public boolean remove( E value ) { if ( !contains( value ) ) return false; root = remove( root, value ); return true; }

// Returns a string representation of this BST. public String toString() { String str = toString( root ); if ( str.endsWith( ", " ) ) str = str.substring( 0, str.length() - 2 ); return "[" + str + "]"; }

// Returns an iterator for this BST. public Iterator iterator() { // Complete method return the iterator; // Fix this!! }

//*************** Private helper methods: *********************

// Returns true if the BST rooted at node contains value; // otherwise returns false (recursive version). private boolean contains( TreeNode node, E value ) { if ( node == null ) return false; else { int diff = ( (Comparable)value ).compareTo( node.getValue() ); if ( diff == 0 ) return true; else if ( diff 0) return contains( node.getRight(), value ); } }

/* // Iterative version: private boolean contains(TreeNode node, E value) { while (node != null) { int diff = ( (Comparable)value).compareTo( node.getValue() ); if (diff == 0) return true; else if (diff 0) node = node.getRight(); } return false; } */

// Adds value to the BST rooted at node. Returns the // root of the new tree. // Precondition: the tree rooted at node does not contain value. private TreeNode add( TreeNode node, E value ) { if ( node == null ) node = new TreeNode( value ); else { int diff = ( (Comparable)value ).compareTo( node.getValue() ); if ( diff 0) node.setRight( add( node.getRight(), value ) ); } return node; }

// Removes value from the BST rooted at node. // Returns the root of the new tree. // Precondition: the tree rooted at node contains value. private TreeNode remove( TreeNode node, E value ) { int diff = ( (Comparable)value ).compareTo( node.getValue() ); if ( diff == 0 ) // base case node = removeRoot( node ); else if ( diff 0) node.setRight( remove( node.getRight(), value ) ); return node; }

// Removes the root of the BST rooted at root // replacing it with the smallest node from the right subtree. // Returns the root of the new tree. private TreeNode removeRoot(TreeNode root) { TreeNode node = root.getRight();

// TODO complete method

return node; }

// Utility routine to print the structure of the BST public void printSideways() { if (root == null) return; printSideways(root, 0); }

// Precondition: original argument != null private void printSideways( TreeNode t, int depth ) { if ( t.getRight() != null ) printSideways( t.getRight(), depth + 1 );

process( t.getValue(), depth );

if ( t.getLeft() != null ) printSideways( t.getLeft(), depth + 1 ); }

// Simply display the toString version of my_data private void process( E obj, int depth ) { for ( int j = 1; j

// Returns a string representation of the tree rooted at node. private String toString( TreeNode node ) { if ( node == null ) return ""; else return toString( node.getLeft() ) + node.getValue() + ", " + toString( node.getRight() ); }

// Implements an Iterator for this tree. private class MyTreeSetIterator implements Iterator { // TODO instance variable(s)

public MyTreeSetIterator( TreeNode root ) { // TODO complete constructor }

public boolean hasNext() { // TODO complete method return false; // Fix this!! }

public E next() { // TODO complete method return null; // Fix this!! }

public void remove() { throw new UnsupportedOperationException(); } }

//************************** main: **************************

public static void main(String[] args) { String[] words = {"One", "Two", "Three", "Four", "Five", "Six", "Seven", "Eight", "Nine", "Ten"}; MyTreeSet bst = new MyTreeSet();

for (String word : words) { System.out.println("Added: " + word + " " + bst.add(word)); System.out.println("Contains: " + word + " " + bst.contains(word)); if(bst.add(word)) System.out.println("*** Added a duplicate value ***"); System.out.println(bst); } bst.printSideways();

System.out.println("Traversal with an iterator:"); for (Object obj : bst) System.out.print(obj + " "); System.out.println();

for (String word : words) { System.out.println("Removed: " + word + " " + bst.remove(word)); if(bst.remove(word)) System.out.println("*** Removed a non-existent value ***"); System.out.println(bst); bst.printSideways(); } } }

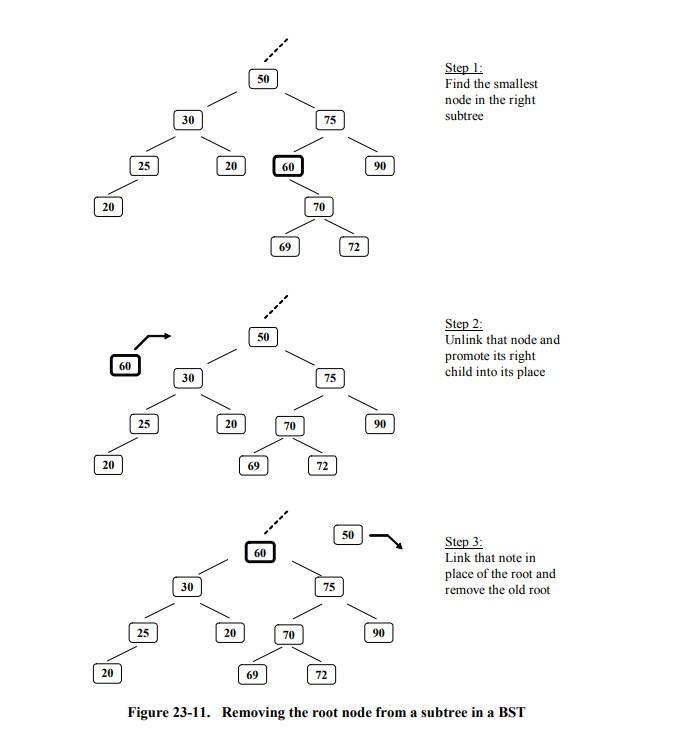
Figure 23-9 shows a fragment from a simple class that implements a BST. The field root refers to the root of the tree. The no-args constructor creates an empty tree by setting root to null. We have provided the contains, add, remove, and tostring methods. This implementation assumes that the nodes of the tree hold Comparable objects, but it would be easy to provide another constructor that takes a comparator as a parameter. Each of our four methods (contains, add, remove, and tostring) uses a respective private recursive helper method, which takes an additional parameter: the root node of a subtree for which the method is called (Figure 23-10). // Implements a BST with TreeNode nodes. public class MyTreeset \{ private TreeNode root; // holds the root of this BST // Constructor: creates an empty BST. public MyTreeset() \{ // Adds value to the BST rooted at node. Returns the root of the // new tree. // Precondition: the tree rooted at node does not contain value. private TreeNode add (TreeNode node, Object value) \{ if (node == nul1) node = new TreeNode (value); else f int diff = ((Comparable( diff 0 ) node. setRight (add (node.getright (), value)); j return node; \} // Removes value from the BST rooted at node. Returns the root // of the new tree. // Precondition: the tree rooted at node contains value. private TreeNode remove(TreeNode node, Object value) \{ int diff = ((Comparable==0 ) node = removeRoot (node) ;// base case else if diff 0 ) node.setright (remove (node.getright (), value)); return node; \} Figure 23-10 MyTreeset.java Continued // Returns a string representation of the tree rooted at node. private string tostring(TreeNode node) ( if (node == null) return ""; else return tostring(node.getLeft ()) + node.getvalue () + ", "+ tostring (node.getRight ()); Figure 23-10. Recursive helper methods in JM\Ch23\BST\MyTreeSet.j ava Actually, the contains, add, and remove methods have simple iterative versions as well, because in these methods at each step we either explore the left subtree or the right subtree, but not both. For example: // Iterative version: private boolean contains(TreeNode node, Object value) \{ while (node I= nul1) \{ int diff = ((Comparable>) value ) compareto (node.getvalue ())); if (diff ==0 ) return true; else if (diff = node getLeft () ; else // if (diff >0 ) node = node get R ight ( ) \} return false; f In our implementation, the add method adds a new node as a leaf, appending it ether as the root (if the tree was empty) or to the left or to the right subtree, depending on the value (Figure 23-10). The remove method is a little more involved. The most complicated part is the base case, when the target value to be removed is found at the root (of some subtree). We have isolated this case into a separate method, removeRoot. It removes the root node and returns a reference to the root of the new tree. The idea of the algorithm is to replace the root with the smallest node in the right subtree. (In a slightly different version, we would replace the root with the largest node in the left subtree.) Such a node can have only one child (right), so it is easy to unlink that node from the tree by promoting its right child into its place. Figure 23-11 illustrates this algorithm. Step 1: Find the smallest node in the right subtree Step 2: Unlink that node and promote its right child into its place Step 3: Link that note in place of the root and remove the old root Figure 23-11. Removing the root node from a subtree in a BST As you can see, the contains, add, and remove methods take, in the worst case, an amount of time proportional to the height of the tree. When the tree is reasonably "bushy," this is O(logn), where n is the number of nodes in the tree. In our simplified implementation, if the values to be added to the BST arrive not in random order but close to ascending or descending order, the tree may lose its shape and deteriorate into an almost linear structure. A more sophisticated implementation would use algorithms that keep the tree "balanced" (but such algorithms are outside the scope of this book). As a lab exercise, fill in the blanks in the removeroot method in Iterable by implementing an iterator method and a MyTreesetiterator class. See Section for an example. Your iterator should perform inorder traversal of the tree: left subtree, root, right subtree. Use a Stack> in your MyTreesetIterator class. Do not implement the remove method for your iterator