Assembly x86 MASM

Write required procedures for computing the results of a cubic equation and graphically displaying the results in the console window. A source file has been included to use as a starting point. You will need to do the following: PART 1: Put in the code for the SolveForAandB procedure (35 points) PART 2: Put in the code for the LinearEquation procedure (15 points) PART 3: Put in code to compute the X increment value. (15 points) PART 4: Put in the code for the CubicEquation procedure. (35 points)

You should all know the equation for a line, y = ax + b. If you know two points on a line, such as defined by x0, y0 and x1,y1, you can solve for a and b. The solution will not be presented here as it is basic math that you should know or be able to reference easily. We need to map from one coordinate space to another using a linear equation like the one above. For our purposes, we are going to rename the variables. First we will rename y to xs, a to ax and b to bx. Then the equation can be written in the form of a high level language statement as shown below. xs = ax * x + bx We will use this to get the xs screen coordinate from the x value used for the range over which we wish to plot our cubic equation. We also need to solve for the ys screen coordinate. The linear equation for that is shown below. ys = ay * y + by The SolveForAandB procedure is used to calculate the values of the a and b coefficients used for mapping. You are given xs0, xs1, x0 and x1 used to solve for ax and bx. Similarly, you are given ys0, ys1, y0 and y1 used for solving for ay and by. Once you have the coefficients for the above linear equations, the LinearEquation procedure is used to compute the screen coordinates. The output of LinearEquation needs to be a byte value, so the solutions it solves for will look like the following. xs = (int)(ax * x + bx) ys = (int)(ay * y + by) Once you have those two procedures working, you can verify that they are producing the right answers by plugging in numbers where you know the solutions. Next you will need to compute a value for xIncr. x will initially be given a starting value of x0 (-10.0). Every time through the loop used for plotting, xIncr is added to the value of x until it reaches x1 (+10.). Lets say the screen allows for 80 characters per line. You would want to set xIncr to a value that allowed 80 positions across the screen to be plotted. Once you have computed xIncr, you should see a plot of a linear equation, y = x as shown below.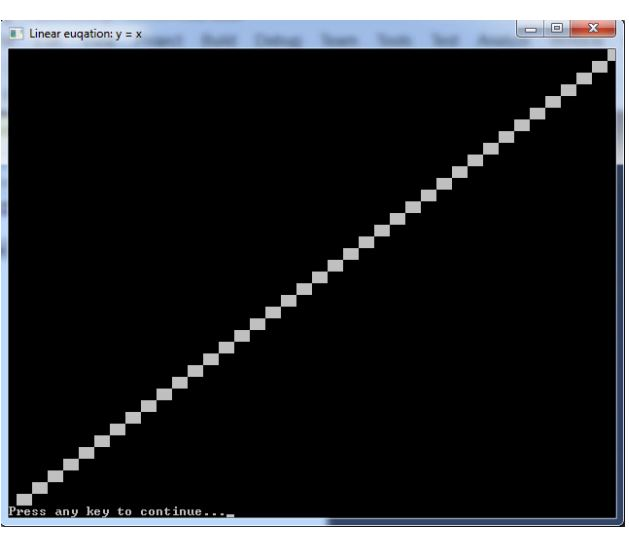

INCLUDE Irvine32.inc

; The prototypes that the Plotter procedure calls are defined here. INCLUDE prototypes.inc

; Local prototypes CubicEquation PROTO, pY:PTR REAL8, x:REAL8 SineFunction PROTO, pY:PTR REAL8, x:REAL8

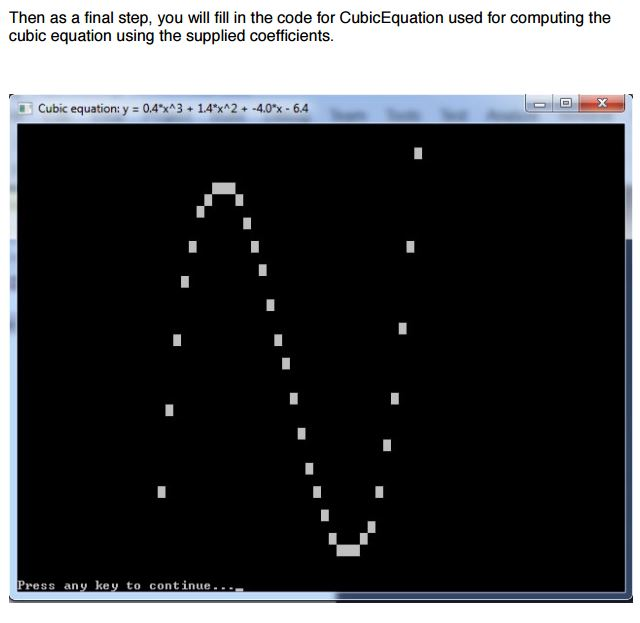
.data ; Cubic equation coefficients coeffA REAL8 0.4 coeffB REAL8 1.4 coeffC REAL8 -4.0 coeffD REAL8 -6.4

windowTitle BYTE "0.4x^3 + 1.4x^2 - 4.0x -6.4",0

; Ranges for cubic plot x0 REAL8 -10.0 x1 REAL8 10.0 y0 REAL8 -10.0 y1 REAL8 10.0

; Ranges for sine function plot xsin0 REAL8 ? xsin1 REAL8 ? ysin0 REAL8 -2.0 ysin1 REAL8 2.0 fval4 REAL8 4.0

.code main PROC ; Initialize the FPU finit

; You can set the foreground and background colors mov eax, yellow + (blue * 16) call SetTextColor

; First develop and debug SolveForAandB ; You can check your values at http://www.webmath.com/equline1.html

; Then develop and debug LinearEquation

; etc.

; You call Plotter with the X & Y ranges, and the offset ; to the procedure calculating the Y values. ; Try this once your procedures are working. ;INVOKE Plotter, x0, x1, y0, y1, OFFSET windowTitle, OFFSET CubicEquation

; You can plot another function in the same program, ; and use different ranges. ; You need to define the xsin0 and xsin1 values to use this. ;INVOKE Plotter, xsin0, xsin1, ysin0, ysin1, OFFSET windowTitle, OFFSET SineFunction

exit main ENDP

;------------------------------------------------------------- ; You can store a floating point value into a location ESI is ; pointing to as follows: ; fstp REAL8 PTR [esi] ;-------------------------------------------------------------

;------------------------------------------------------------- SolveForAandB PROC USES esi, xReal0:REAL8, ; x0 as real xReal1:REAL8, ; x1 as real yReal0:REAL8, ; y0 as real yReal1:REAL8, ; y1 as real pA:PTR REAL8, ; Pointer to A for storing result pB:PTR REAL8 ; Pointer to B for storing result ; Returns A and B coefficients for linear equation. ;------------------------------------------------------------- ; PART 1: Put in the code for the SolveForAandB procedure ; The following is needed to keep the assembler from complaining ; Remove it and put in your code for the cubic function. fld xReal0 fstp xReal0 fld xReal1 fstp xReal1 fld yReal0 fstp yReal1 mov esi, pA mov esi, pB

ret SolveForAandB ENDP

;---------------------------------------------------------- LinearEquation PROC USES esi eax, pYReal:PTR REAL8, ; Pointer to y as real value xReal:REAL8, ; x as real value a:REAL8, b:REAL8 ; ; Computes the following equation: ; y = a * x + b ;---------------------------------------------------------- ; PART 2: Put in the code for the LinearEquation procedure ; Remove the following and put in your code for the linear equation

; y = x fld xReal mov esi, pYReal fstp REAL8 PTR [esi]

; The following is needed to stop the assembler from complaining fld a fstp a fld b fstp b

ret LinearEquation ENDP

Linear euqation: y 3x Press any key to continue