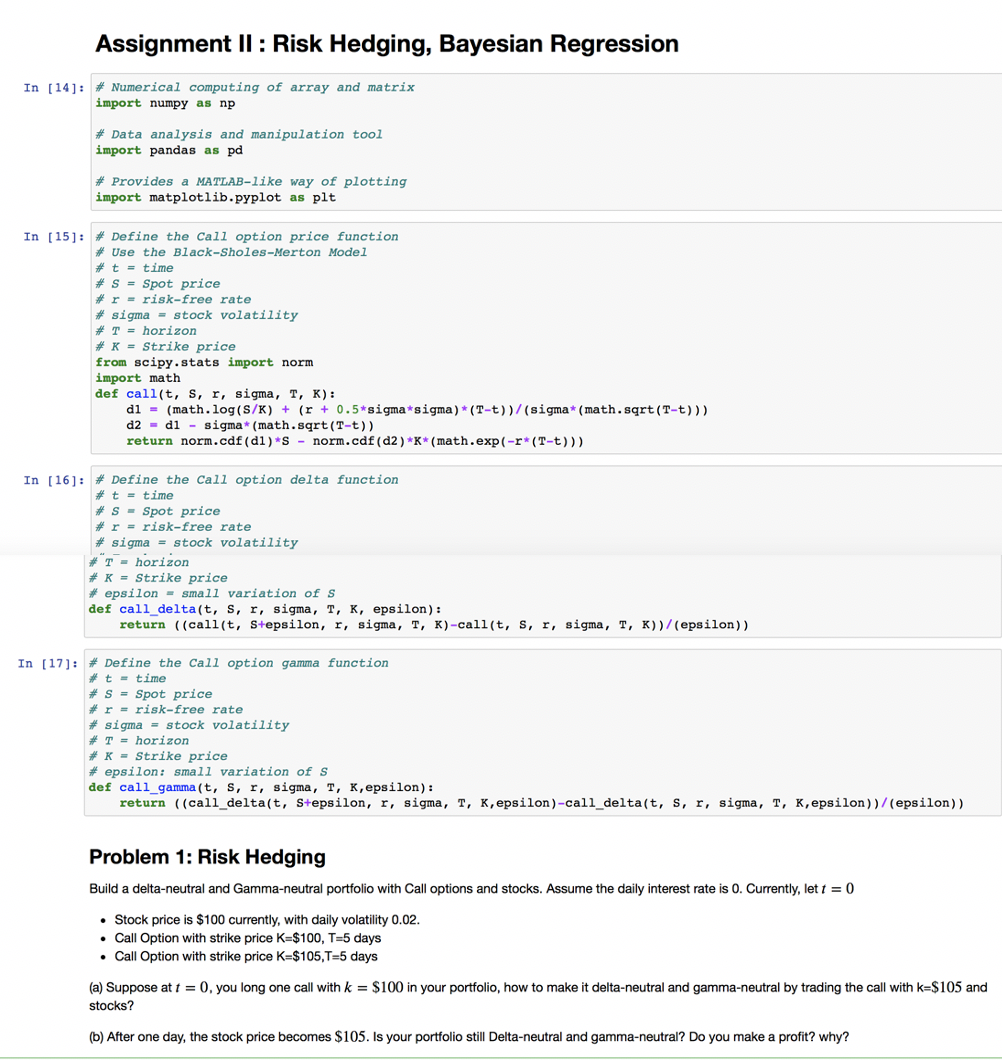
Assignment II : Risk Hedging, Bayesian Regression In [14]: # Numerical computing of array and matrix import numpy as np # Data analysis and manipulation tool import pandas as pd # Provides a MATLAB-like way of plotting import matplotlib.pyplot as plt In [15]: Define the call option price function # Use the Black-Sholes-Merton Model t = time # S = Spot price * r = risk-free rate #sigma = stock volatility # T = horizon Strike price from scipy.stats import norm import math def call(t, s, r, sigma, T, K): di = (math.log(S/K) + (r + 0.5*sigma*sigma)*(T-t))/(sigma* (math.sqrt(T-t))) d2 = di sigma* (math.sqrt(T-t)) return norm.cdf (dl)*s - norm.cdf (d2 )*K* (math.exp(-r*(T-t))) In [16]: # Define the Call option delta function # t = time * S - Spot price # r = risk-free rate #sigma = stock volatility #T - horizon # K = Strike price #epsilon - small variation of S def call_delta(t, s, r, sigma, T, K, epsilon): return ((call(t, Stepsilon, r, sigma, T, K)-call(t, s, r, sigma, T, K))/(epsilon)) In [17]: # Define the call option gamma function # t = time # S = Spot price # r = risk-free rate # sigma = stock volatility # T - horizon # K - Strike price #epsilon: small variation of S def call_gamma(t, s, r, sigma, T, K, epsilon): return ((call_delta(t, Stepsilon, r, sigma, T, K, epsilon)-call_deltat, s, r, sigma, T, K, epsilon))/(epsilon)) Problem 1: Risk Hedging Build a delta-neutral and Gamma-neutral portfolio with Call options and stocks. Assume the daily interest rate is 0. Currently, let t = 0 Stock price is $100 currently, with daily volatility 0.02. Call Option with strike price K=$100, T-5 days Call Option with strike price K=$105,T=5 days (a) Suppose at t = 0. you long one call with k = $100 in your portfolio, how to make it delta-neutral and gamma-neutral by trading the call with k=$105 and stocks? (b) After one day, the stock price becomes $105. Is your portfolio still Delta-neutral and gamma-neutral? Do you make a profit? why? Assignment II : Risk Hedging, Bayesian Regression In [14]: # Numerical computing of array and matrix import numpy as np # Data analysis and manipulation tool import pandas as pd # Provides a MATLAB-like way of plotting import matplotlib.pyplot as plt In [15]: Define the call option price function # Use the Black-Sholes-Merton Model t = time # S = Spot price * r = risk-free rate #sigma = stock volatility # T = horizon Strike price from scipy.stats import norm import math def call(t, s, r, sigma, T, K): di = (math.log(S/K) + (r + 0.5*sigma*sigma)*(T-t))/(sigma* (math.sqrt(T-t))) d2 = di sigma* (math.sqrt(T-t)) return norm.cdf (dl)*s - norm.cdf (d2 )*K* (math.exp(-r*(T-t))) In [16]: # Define the Call option delta function # t = time * S - Spot price # r = risk-free rate #sigma = stock volatility #T - horizon # K = Strike price #epsilon - small variation of S def call_delta(t, s, r, sigma, T, K, epsilon): return ((call(t, Stepsilon, r, sigma, T, K)-call(t, s, r, sigma, T, K))/(epsilon)) In [17]: # Define the call option gamma function # t = time # S = Spot price # r = risk-free rate # sigma = stock volatility # T - horizon # K - Strike price #epsilon: small variation of S def call_gamma(t, s, r, sigma, T, K, epsilon): return ((call_delta(t, Stepsilon, r, sigma, T, K, epsilon)-call_deltat, s, r, sigma, T, K, epsilon))/(epsilon)) Problem 1: Risk Hedging Build a delta-neutral and Gamma-neutral portfolio with Call options and stocks. Assume the daily interest rate is 0. Currently, let t = 0 Stock price is $100 currently, with daily volatility 0.02. Call Option with strike price K=$100, T-5 days Call Option with strike price K=$105,T=5 days (a) Suppose at t = 0. you long one call with k = $100 in your portfolio, how to make it delta-neutral and gamma-neutral by trading the call with k=$105 and stocks? (b) After one day, the stock price becomes $105. Is your portfolio still Delta-neutral and gamma-neutral? Do you make a profit? why