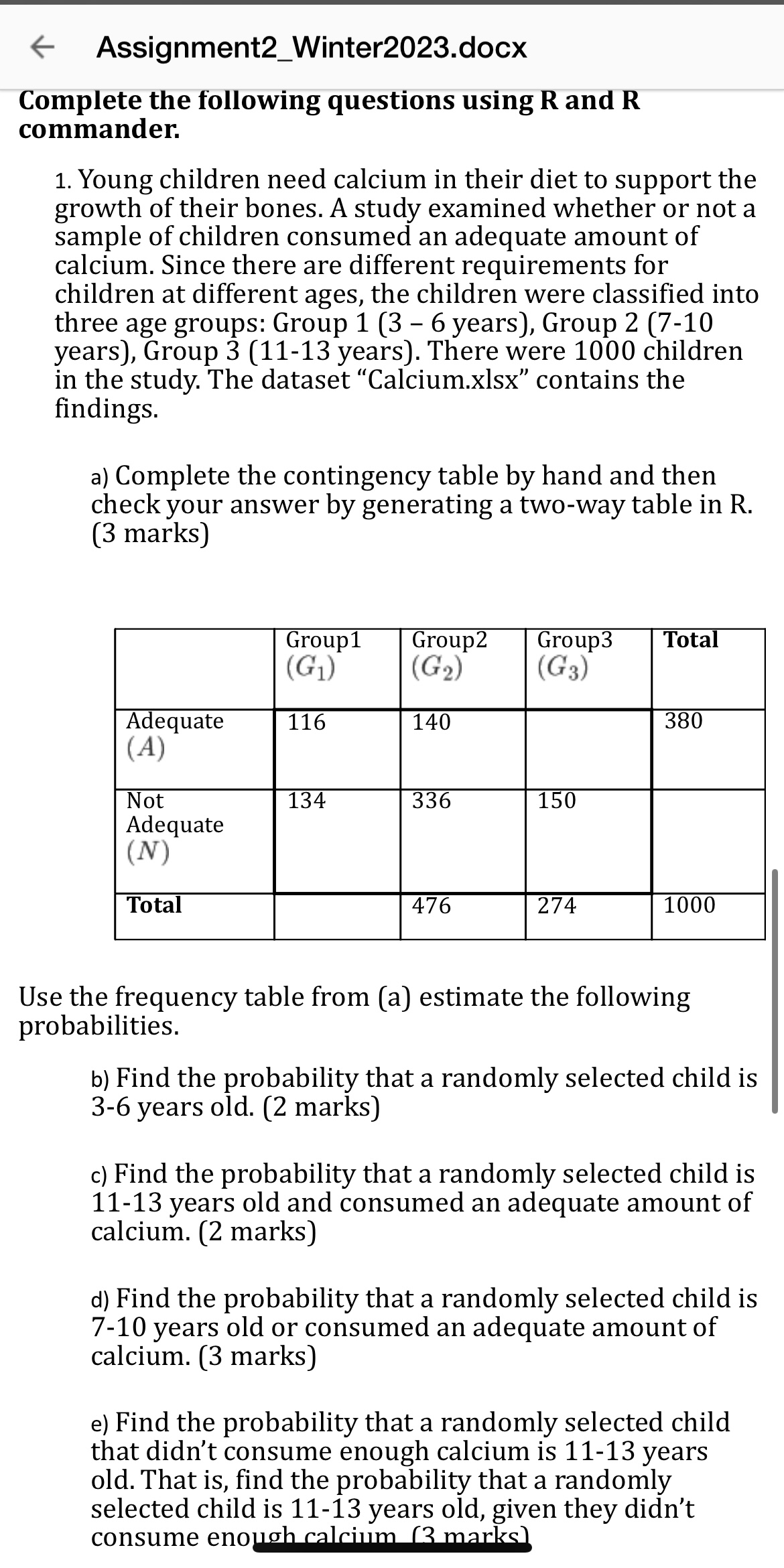
Assignment2_Winter2023.docx c) What is the insurance company's mean cash intake? (2 marks) d) Suppose the insurance company insures one hundreds 25-year-old men under the terms of Question b). What is the probability that the insurance company will receive at least one claim? For simplicity, assume independence. (3 marks) 5. Three friends are trying to predict who will make more money at work tomorrow. John works construction: he will make $250 tomorrow unless it rains, in which case he will make $0. Sara works in a restaurant: she will earn $100 if it is sunny, $200 if it is rainy, and $250 if the weather is average. Chris works in a warehouse, and he earns a flat rate of $200 per day, regardless of weather conditions. Suppose there is a 20% chance that tomorrow will be sunny, and 50% chance that the weather will be average, and a 30% chance of rain. John (Construction) Sunny $250 Average $250 Rainy $0 Sara (Restaurant) Chris (Warehouse) $100 $200 $250 $200 $200 $200 a) Determine tomorrow's expected earnings for each of these 3 friends. (6 marks) b) Compute the standard deviation for Sara's earnings. (3 marks) 6. Courtney is a basketball player who makes 65% of her free throws. She attempts 10 free throws. Part B a) What is the probability that she will miss more than 8 of them? (4 marks) b) What is the probability that she will miss at least 2 of them? (4 marks) c) How many throws do you expect Courtney will miss? (2 marks) d) Obtain the standard deviation of the number of throws that Courtney misses. (2 marks) Assignment2_Winter2023.docx Part A 1. The blood types of a group of 3 people are O, A, and B, respectively. Suppose two people are randomly selected with replacement (that is, a person is selected and his/her blood type is observed. This person then returns to the group). Let A be the event of selecting a person of type A, B be the event of selecting a person of type B, and O be the event of selecting a person of type O. a) List all possible outcomes. (2 marks) b) List all possible outcomes for each of the following events and find the corresponding probabilities. (8 marks) i. E1 = {Exactly 1 person of type A is drawn} ii. E2 = {The first person has type B} iii. E3 = {At least one person has type 0} iv. E4 = {Both people have the same blood type} List all possible outcomes and find the probabilities of the following events. (10 marks: 2 for each) c) List all possible outcomes and find the probabilities of the following events. (10 marks: 2 for each) i. Not E3 ii. E1 & E3 iii. E1 & E4 iv. E2 & E4 v. E3 or E4 d) Identify all possible pairs of events defined in part (b) that are mutually exclusive. (3 marks) e) Verify mathematically that E2 and E4 are independent events, while E3 and E4 are not. (3 marks) 2. Suppose we select a random sample of 3 numbers between 1 and 40, sampling without replacement. a) How many samples of size 3 are possible? (2 marks) b) What is the probability that the sum of the values in our sample is less than 11? (3 marks) f) Find the probability that a randomly selected 11-13 years old child didn't consume enough calcium. (3 marks) g) Are events N and G3 independent? Explain your answer. (2 marks) h) Are events A and G3 mutually exclusive? Explain your answer. (2 marks) Question 2 uses the data set "Insurance.xlsx," which contains information regarding 1338 policy holders of an insurance company; download this data set and use R commander to complete the following tasks. For each question, copy or take a screenshot of the output in R commander and submit it with your solutions to each question. To save space, you only need to copy and paste what is asked for in the questions and should adjust the size of the image when appropriate. 2. Use R commander to obtain the most appropriate table to answer the following questions. Hint: construct a frequency distribution in part (a), and contingency tables in parts b through f. a) If we randomly select a policy holder, what is the probability that they are a smoker? (2 marks) b) If we randomly select a policy holder, what is the probability that they are a female and a smoker? (2 marks) c) If we randomly select a female, what is the probability that she is a smoker? (4 marks) d) If we randomly select a non-smoker, what is the probability that they are a male and from the southwest? (4 marks) e) If we randomly select a policy holder, what is the probability they live in the southwest or are a smoker, given they are male? (4 marks) f) If we randomly select a male smoker, what is the probability that he is from a southwest region. (4 marks) Assignment2_Winter2023.docx STAT 151 Assignment 2 Total: 113 Marks STAT 151 Assignment 2 Due date: refer to the Course Outline Purposes This assignment has two parts. The following questions assess your ability to identify the sample space of a chance experiment, calculate probabilities using the equally likely outcome model, and the addition, complementation, conditional probability, and multiplication rules, determine if two events are independent by calculation, and apply counting rules. This assignment also assesses your understanding of discrete probability distributions, your ability to find the mean (expected value) and the standard deviation of a discrete random variable and your ability to identify and work with binomial random variables. The second part assesses your ability to use R commander to compute the probabilities listed above. Instructions For every assignment in this course, you are required to complete the questions or tasks in Part A by hand. This means that to do any calculation or drawing, you will NOT use R commander or any computer application. That is, you are meant to do the calculations manually with a non-programmable scientific calculator and use a pen or pencil to draw figures or build a distribution table on paper (or on an iPad/tablet). Then you will submit a photo of your written solution using the appropriate submission box on the corresponding Crowdmark submission page. Before you complete Part B using R commander, you should read and practice the R commander steps by following the related examples in the Lab Manual and the Demos, which you can download via a link in the Course Content folder on mskans. Assignment2_Winter2023.docx Complete the following questions using R and R commander. 1. Young children need calcium in their diet to support the growth of their bones. A study examined whether or not a sample of children consumed an adequate amount of calcium. Since there are different requirements for children at different ages, the children were classified into three age groups: Group 1 (3 - 6 years), Group 2 (7-10 years), Group 3 (11-13 years). There were 1000 children in the study. The dataset "Calcium.xlsx" contains the findings. a) Complete the contingency table by hand and then check your answer by generating a two-way table in R. (3 marks) Group1 (G1) Group2 (G2) Group3 Total (G3) Adequate 116 140 380 (A) Not 134 336 150 Adequate (N) Total 476 274 1000 Use the frequency table from (a) estimate the following probabilities. b) Find the probability that a randomly selected child is 3-6 years old. (2 marks) c) Find the probability that a randomly selected child is 11-13 years old and consumed an adequate amount of calcium. (2 marks) d) Find the probability that a randomly selected child is 7-10 years old or consumed an adequate amount of calcium. (3 marks) e) Find the probability that a randomly selected child that didn't consume enough calcium is 11-13 years old. That is, find the probability that a randomly selected child is 11-13 years old, given they didn't consume enough calcium (3 marks) 3. Recall from part A that Courtney makes 65% of her free throws. she attempts 100 free throws. Submission a) What is the probability that she will miss at most 40 of them? (2 marks) b) What is the probability that she will miss at least 20 of them? (3 marks) c) What is the probability that the number of throws that she will miss is at least 25 and at most 35? (3 marks) Submit your work by accessing the Crowdmark email (or Crowdmark link on mskans) to submit Assignment 2. Please ensure that each picture properly oriented and easy to read (not fuzzy, not too small, and not taken in a dark room so that it is difficult to read). All work must be submitted to Crowdmark by 6:00 PM on the due date. DO NOT submit your work to mskans. Avoiding Plagiarism: If you submit an assignment, you are claiming it is your work. Do not allow any part of your work to be copied by anyone else. Where two or more assignments are found to be unreasonably similar, either in whole or in part, and no assistance has been acknowledged, all parties involved are liable to a score of zero on the assignment. MacEwan University's academic policies are available at: https://www.macewan.ca/contribute/groups/public/documents/policy/zwdf/c g9s/~edisp/student_acad_integ_policy.pdf Assignment2_Winter2023.docx 3. There are four ABO blood types: A, B, AB and O. Your blood type is also determined by RH status: Rh+ or Rh-. That leaves us with eight possible blood types: A+, A-, B+, B-, AB+, AB-, O+, 0-. Among a group of 50 patients, 18 of them have type A+, 3 have type A-, 4 have B+, 2 have B-, 4 have AB+, 2 has AB-, 13 have type 0+, and 4 have type O-. A random sample of 8 patients will be selected from this group. a) How many different samples are possible? (2 marks) b) How many different samples of size 8 are possible subject to the constraint that no 2 patients may have the same blood type? (2 marks) c) What is the probability that a random sample of 8 patients from this group has no two patients with the same blood type? (2 marks) 4. Assume that a 25-year-old man has these probabilities of dying during the next five years: Age at death 25 26 27 28 29 Probability 0.00039 0.00044 0.00051 0.00060 0.00057 a) What is the probability that the man does not die in the next five years? (2 marks) b) An online insurance site offers a term insurance policy that will pay $100,000 if a 25-year-old man dies within the next five years. The cost is $175 per year. So the insurance company will take in $875 from this policy if the man does not die within five years. If he does die, the company must pay $100,000. Let X denote the cash intake of the insurance company which depends on how many premiums the man paid. Find the distribution of X. (3 marks) Hint: if a 25-year-old man dies in the first year, the cash intake of the insurance company is -(100,000-175)=-$99,825 under the policy; if he dies in the second year, the cash intake of the company is -(100,000-2*175) = -$99,650 etc. If the man does not die within five years, the cash intake of the company is 5*175=875.