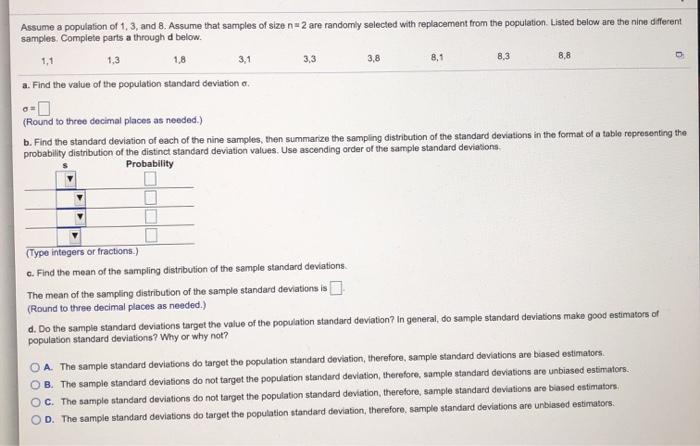
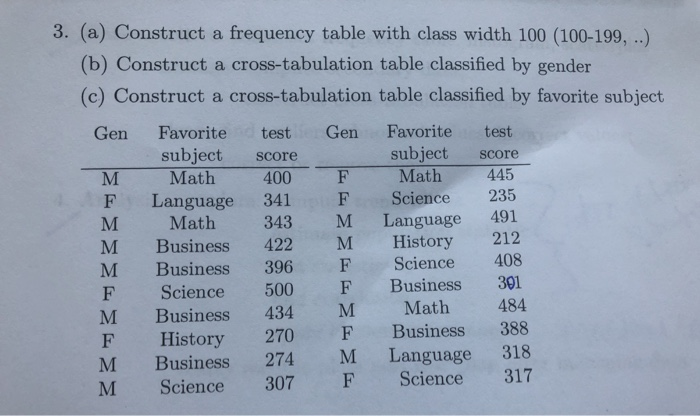
Assume a population of 1, 3, and 8. Assume that samples of size n= 2 are randomly selected with replacement from the population. Listed below are the nine different samples. Complete parts a through d below. 1.1 1,3 1,8 3.1 3,3 3.8 8,1 8.3 8.8 a. Find the value of the population standard deviation a. (Round to three decimal places as needed.) b. Find the standard deviation of each of the nine samples, then summarize the sampling distribution of the standard deviations in the format of a table representing the probability distribution of the distinct standard deviation values. Use ascending order of the sample standard deviations, Probability 0 (Type integers or fractions.) c. Find the mean of the sampling distribution of the sample standard deviations. The mean of the sampling distribution of the sample standard deviations is| (Round to three decimal places as needed.) d. Do the sample standard deviations target the value of the population standard deviation? In general, do sample standard deviations make good estimators of population standard deviations? Why or why not? A. The sample standard deviations do target the population standard deviation, therefore, sample standard deviations are biased estimators. O B. The sample standard deviations do not target the population standard deviation, therefore, sample standard deviations are unbiased estimators.. O C. The sample standard deviations do not target the population standard deviation, therefore, sample standard deviations are biased estimators, O D. The sample standard deviations do target the population standard deviation, therefore. sample standard deviations are unbiased estimators.3. (a) Construct a frequency table with class width 100 (100-199, ..) (b) Construct a cross-tabulation table classified by gender (c) Construct a cross-tabulation table classified by favorite subject Gen Favorite test Gen Favorite test subject score subject score M Math 400 F Math 445 F Language 341 Science 235 M Math 343 M Language 491 M Business 422 M History 212 M Business 396 Science 408 F Science 500 Business 301 M Business 434 M Math 484 F History 270 F Business 388 M Business 274 M Language 318 M Science 307 F Science 317Question 2 (4 points) TIMES (days) Activity Start Finish OPTIMISTIC MOST LIKELY PESSIMISTIC Node Node to m Ip A 1 2 25 34 61 B 1 3 21 27 39 C 2 5 18 42 66 D 3 4 32 50 58 E 4 5 8 20 44 Given the Activity on Arrow Diagram and the data found in the table above, calculate each of the following values: Activity A.........te = 37 Standard Deviation = 6 Activity B.........te = A/ Standard Deviation = A/d. Do the sample standard deviations target the value of the population standard deviation? In general, do sample standard deviations make good estimators of population standard deviations? Why or why not? OA. The sample standard deviations do target the population standard deviation, therefore, sample standard deviations are unbiased estimators. OB. The sample standard deviations do target the population standard deviation, therefore, sample standard deviations are biased estimators. Oc. The sample standard deviations do not target the population standard deviation, therefore, sample standard deviations are biased estimators. OD. The sample standard deviations do not target the population standard deviation, therefore, sample standard deviations are unbiased estimators.The following figure shows the normal distribution with the proportion of the area under the normal curve contained within one, two, and three standard deviations of the mean. The last proportion on each side, 0.13%, depicts the remaining area under the curve. Specifically, 0.13% of the area under the standard normal distribution is located above z-score values greater than the mean () plus three standard deviations (+30). Also, because the normal distribution is symmetrical, 0.13% of the area under the standard normal distribution is located below z-score values less than the mean () minus three standard deviations (-30). 34.13% 34.13% 13.59% 13.59% 2.15% 2.15% 0.13% 0.13% -30 -20 -10 +10 +20 +30 O Use the figure to help you answer the following questions. The National Assessment of Educational Progress (NAEP) is a nationwide assessment of students' proficiency in nine subjects: mathematics, reading, writing, science, the arts, civics, economics, geography, and U.S. history. The main NAEP assessments are conducted annually on samples of students from grades 4, 8, and 12. In 2002, the reading scores for female students had a mean of 269 with a standard deviation of 33. Assume that these scores are normally distributed with the given mean and standard deviation. A score of 203 is below the mean, while a score of 335 is above the mean. This means that the percentage of female students with scores between 203 and 335 is A score of 368 is above the mean. As a result, the percentage of female students with scores below 368 is You can infer that 84.13% of the female students have scores above