Assume an investor begins saving for retirement at age 25 and retires at age 65. Each year, she contributes $10,000 to her retirement account. To keep things simple, assume that there are 40 annual contributions that occur on the investor's 25-th, 26-th, ...,64-th birthdays, and that the final retirement wealth is determined on the investor's 65-th birthday. 1 Savings are invested as follows: 50% in a broad stock market index and 50% in T-Bills. 

 Your task is to compute the accumulated real retirement savings at age 65 for different return realizations. As explained below, you will generate returns using a Monte Carlo simulation. Here, you can find an Excel file containing historical net returns on the S&P 500 and 3-month T-bills, as well as the consumer price index (CPI) from 1926 to 2017. The return on the CPI serves as a measure of inflation. 

 

STEPS: 

1. Compute the annual real return on the 50/50 portfolio for each year in the sample. The resulting set of 92 portfolio returns represents the empirical distribution. These are the returns investors historically realized when investing in a 50/50 mix of stocks and T-bills over this time period. 

 2. We will use the historical data to assess what may happen in the future via a Monte Carlo simulation. To generate a possible path of future returns, draw 40 times with replacement from the empirical distribution.2 Assuming the 92 historical returns and  a random draw can be generated with  The set of 40 draws you generated can be viewed as one scenario of what may happen in the next 40 years. 

 3. Using the simulated return path, compute the investor's wealth at age 65. 

 ((Assume that no additional contribution is made on the 65-th birthday))

((Recall that this procedure is valid under the assumption that returns are independently and identically distributed (i.i.d.). In other words, we assume that each of the return realizations computed in step one represents an equally likely draw from the same distribution of possible returns.))

 4. Repeat steps two and three 1, 000 times. The most efficient way of doing so in Excel is to use a data table. 

 

QUESTIONS: 

A) Report the mean and standard deviation of the portfolio returns computed in step one. 

 B) Report the mean, standard deviation, 25th and 75th percentiles, minimum, and maximum as well as a histogram of the 1, 000 values you generated for the retirement savings at age 65. Interpret each of these statistics, i.e. explain in words what they tell you in the context of the example. 

 C) Assuming a 50/50 mix of both assets, what amount would the investor need to save annually such that her retirement savings are at least $1m with a probability of 75%? [Hint: (1) To find this number, make an input cell for the annual savings and use trial-and-error to determine the required amount. (2) The number you find will only be approximate because of simulation noise - that is okay!. (3) Goal-seek or solver will not work in this context.] 

 D) Assuming annual savings of $10,000, what mix of the two assets ensures that the investor's savings amount to $1.5m on average? How do the standard deviation and the minimum savings change in this case relative to the baseline scenario of a 50/50 mix?

[Hint: (1) To find the necessary mix, make an input cell for the asset mix and use trial-and-error to determine the required amount. (2) The number you find will only be approximate because of simulation noise - that is ok!. (3) Goal-seek or solver will not work in this context.]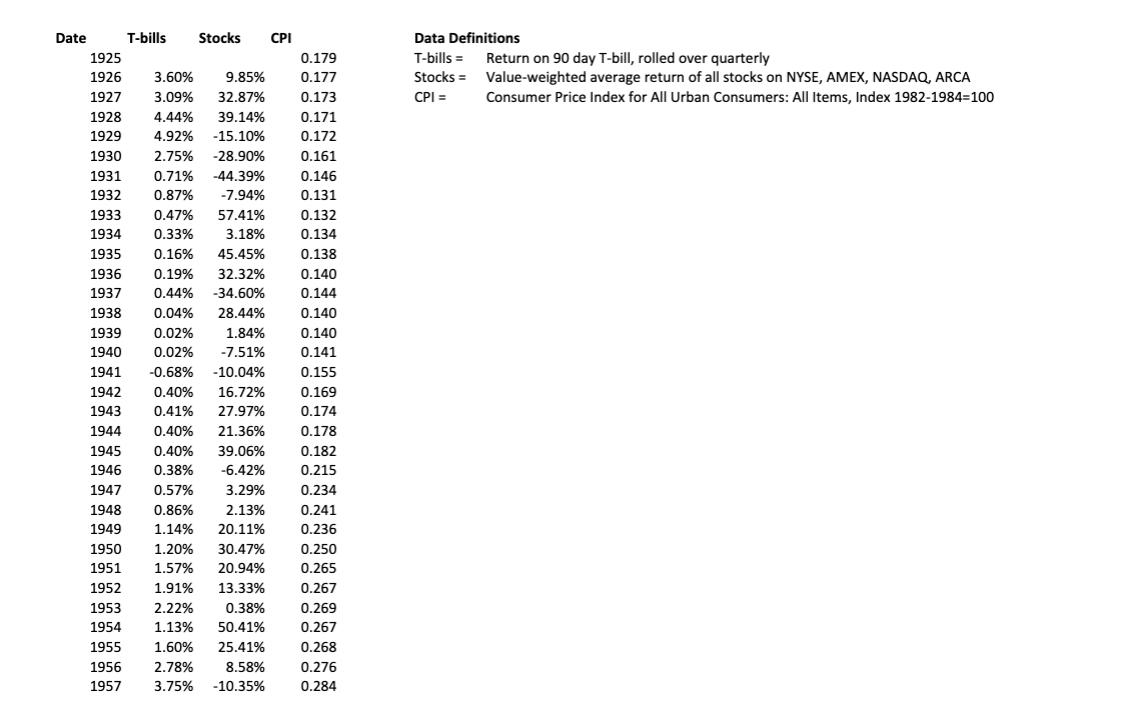   

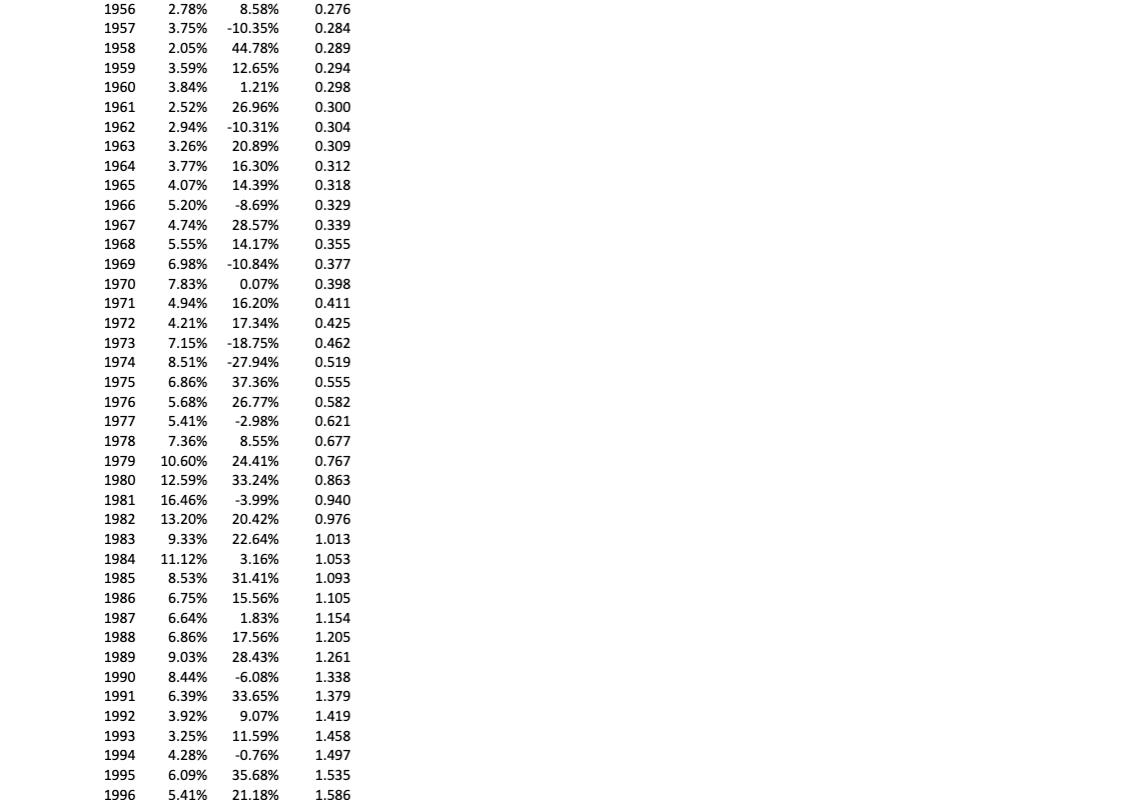
Transcribed Image Text:

Date 1925 1926 T-bills Stocks CPI 3.60% 9.85% 1927 3.09% 32.87% 1928 4.44% 39.14% 1929 4.92% -15.10% 1930 2.75% -28.90% 1931 0.71% -44.39% 1932 0.87% -7.94% 1933 1934 0.33% 1952 1953 1954 0.47% 57.41% 3.18% 0.16% 45.45% 1935 1936 0.19% 32.32% 1937 0.44% -34.60% 1938 0.04% 28.44% 1939 0.02% 1.84% 1940 0.02% -7.51% 1941 -0.68% -10.04% 1942 0.40% 16.72% 1943 0.41% 27.97% 1944 0.40% 21.36% 1945 0.40% 39.06% 1946 0.38% -6.42% 0.57% 1947 3.29% 1948 0.86% 2.13% 1949 1.14% 20.11% 1950 1.20% 30.47% 0.250 1951 1.57% 20.94% 0.265 1.91% 13.33% 0.267 0.269 0.267 2.22% 0.38% 1.13% 50.41% 1.60% 25.41% 0.179 0.177 0.173 0.171 0.172 0.161 0.146 0.131 0.132 0.134 0.138 0.140 0.144 0.140 0.140 0.141 0.155 0.169 0.174 0.178 0.182 0.215 0.234 0.241 0.236 1955 1956 2.78% 8.58% 1957 3.75% -10.35% 0.268 0.276 0.284 Data Definitions T-bills = Stocks = CPI = Return on 90 day T-bill, rolled over quarterly Value-weighted average return of all stocks on NYSE, AMEX, NASDAQ, ARCA Consumer Price Index for All Urban Consumers: All Items, Index 1982-1984-100 Date 1925 1926 T-bills Stocks CPI 3.60% 9.85% 1927 3.09% 32.87% 1928 4.44% 39.14% 1929 4.92% -15.10% 1930 2.75% -28.90% 1931 0.71% -44.39% 1932 0.87% -7.94% 1933 1934 0.33% 1952 1953 1954 0.47% 57.41% 3.18% 0.16% 45.45% 1935 1936 0.19% 32.32% 1937 0.44% -34.60% 1938 0.04% 28.44% 1939 0.02% 1.84% 1940 0.02% -7.51% 1941 -0.68% -10.04% 1942 0.40% 16.72% 1943 0.41% 27.97% 1944 0.40% 21.36% 1945 0.40% 39.06% 1946 0.38% -6.42% 0.57% 1947 3.29% 1948 0.86% 2.13% 1949 1.14% 20.11% 1950 1.20% 30.47% 0.250 1951 1.57% 20.94% 0.265 1.91% 13.33% 0.267 0.269 0.267 2.22% 0.38% 1.13% 50.41% 1.60% 25.41% 0.179 0.177 0.173 0.171 0.172 0.161 0.146 0.131 0.132 0.134 0.138 0.140 0.144 0.140 0.140 0.141 0.155 0.169 0.174 0.178 0.182 0.215 0.234 0.241 0.236 1955 1956 2.78% 8.58% 1957 3.75% -10.35% 0.268 0.276 0.284 Data Definitions T-bills = Stocks = CPI = Return on 90 day T-bill, rolled over quarterly Value-weighted average return of all stocks on NYSE, AMEX, NASDAQ, ARCA Consumer Price Index for All Urban Consumers: All Items, Index 1982-1984-100

Answer rating: 100% (QA)

To compute the accumulated real retirement savings at age 65 for different return realizations well follow the steps provided Step 1 Compute the annua... View the full answer