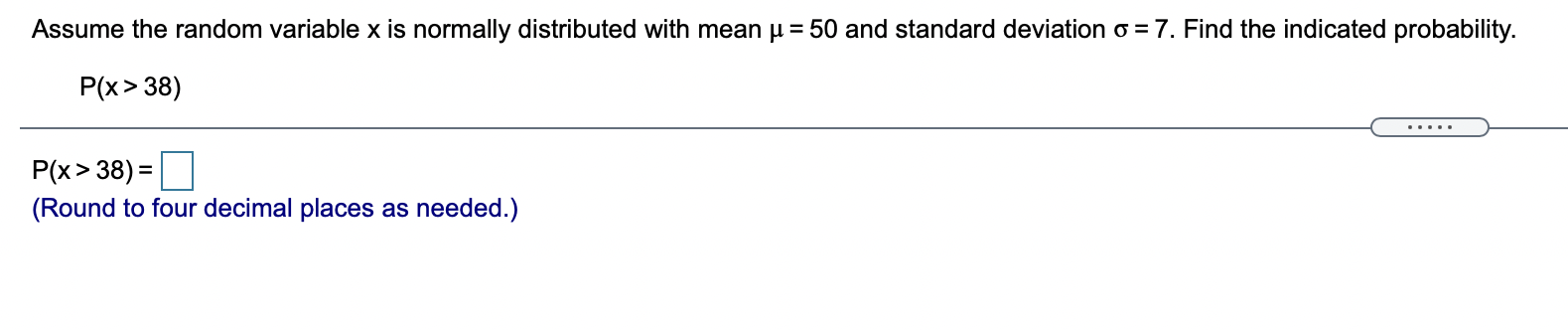
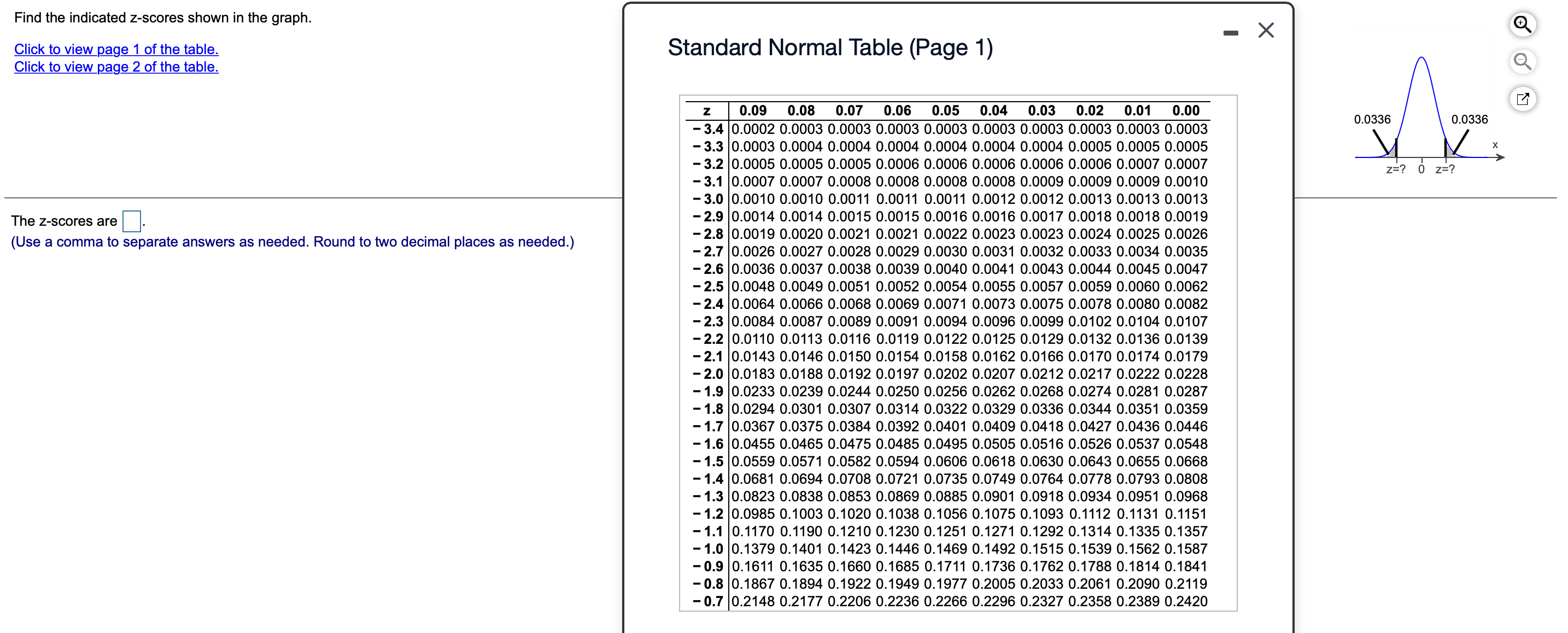
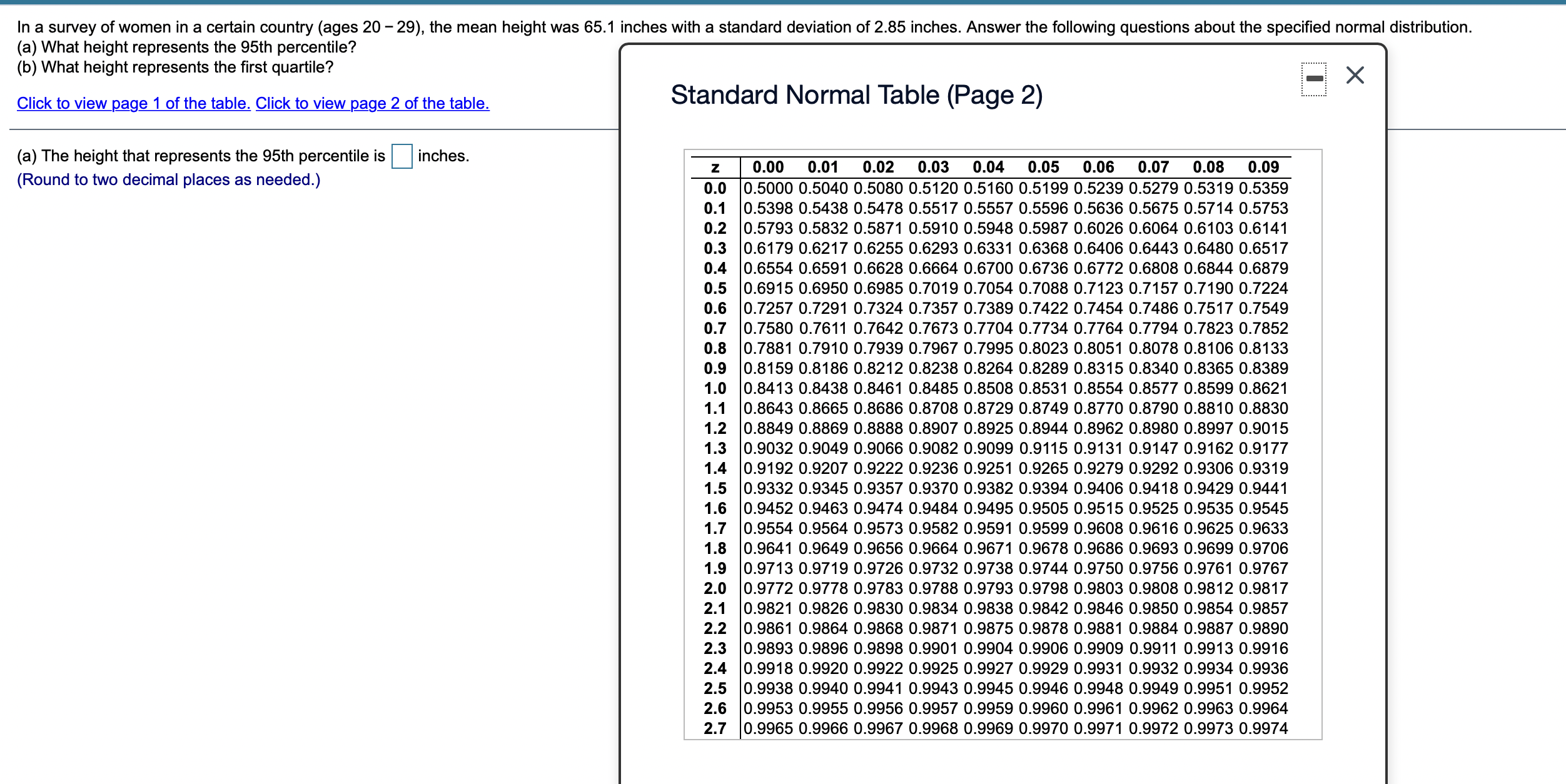
Assume the random variable x is normally distributed with mean u = 50 and standard deviation 6 = 7. Find the indicated probability. P(x > 38) P(x > 38) = D (Round to four decimal places as needed.) Assume the random variable x is normally distributed with mean u = 83 and standard deviation 0 = 5. Find the indicated probability. P(69 01234567891011 Observation number A liquid-dispensing machine has been designed to fill bottles with 1.0 liter of liquid. The standard deviation of the process Is the process in control or out of control? Choose the correct answer below. is 0.2 liter. A control chart is shown. The chart has horizontal lines drawn at the mean, u, at u 1 20, and at u 1 30. Determine if the process shown is in control or out of control. Explain. O A. In control, because none of the three warning signals detected a change. Liquid Dispenser O B. Out of control, because there are nine consecutive points either above or below the mean. O C. Out of control, because a point lies more than three standard deviations from the mean. N O D. Out of control, because two out of three consecutive points lie more than two standard deviations from the mean. Liquid dispensed (in liters) 8 9 10 11 Observation numberIn a survey of a group of men, the heights in the 20-29 age group were normally distributed, with a mean of 68.8 inches and a standard deviation of 2.0 inches. A study participant is randomly selected. Complete parts (a) through (d) below. (a) Find the probability that a study participant has a height that is less than 65 inches. The probability that the study participant selected at random is less than 65 inches tail is . (Round to four decimal places as needed.) Use the normal distribution to the right to answer the questions. Standardizesdogtraes; Composite 9' (a) What percent of the scores are less than 197 (b) Out of 1500 randomly selected scores, about how many would be expected to be greater than 21? (a) The percent of scores that are less than 19 is %t (Round to two decimal places as needed.) Agear has been designed to have a diameter of 3 inches. The standard deviation of the process is 0.5 inch. A control chart is shown. Each chart has horizontal lines drawn at the mean, u, p126, and at pt 36. Determine if the process shown is in control or out of control. Explain. Diameter (inches) n Gears > Muss 1 > 01234567891011 Observation number Q a D\" Is the process in control or out of control? Select all that apply. A. Out of control, because a point lies more than three standard deviations beyond the mean. B. In control, because none of the three warning signals detected a change. 0. D Out of control, because there are nine consecutive points either above or below the mean. . Out of control, because two out of three consecutive points lie more than two standard deviations from the mean. Use the standard normal table to find the z-soore that corresponds to the cumulative area 0.7749. If the area is not in the table, use the entry closest to the area, It the area is halfway between two entries, use the z-soore halfway between the corresponding zscores. Click to view [age 1 of the standard normal table. Click to view p_age 2 ofthe standard normal table. z = (Type an integer or decimal rounded to three decimal places as needed.) Use a table of cumulative areas under the normal curve to find the z-score that corresponds to the given cumulative area. If the area is not in the table, use the entry closest to the area. If the area is halfway between two entries, use the z-score halfway between the corresponding z-scores. If convenient, use technology to find the z-score. 0.052 Click to view page 1 of the table. Click to view page 2 of the table. . . . . . The cumulative area corresponds to the z-score of. (Round to three decimal places as needed.)Use the standard normal table to nd the z-soore that corresponds to the given percentile. If the area is not in the table, use the entry closest to the area. If the area is halfway between two entries, use the z-score halfway between the corresponding z-scores, If convenient, use technology to nd the z-score. P1 Click to view p_age 1 of the table. Click to view p_age 2 of the table. The z-score that corresponds to P1 is . (Round to two decimal places as needed.) Use the standard normal table to nd the z-score that corresponds to the given percentile. If the area is not in the table, use the entry closest to the area. If the area is halfway between two entries, use the z-score halfway between the corresponding z-soores. If convenient, use technology to nd the z-score. P90 Click to view lags 1 of the table. Click to view page 2 of the table, The z-soore that corresponds to P90 is (Round to two decimal places as needed.) Use the standard normal table to nd the z-soore that corresponds to the given percentile. If the area is not in the table, use the entry closest to the area. If the area is halfway between two entries, use the z-soore halfway between the corresponding z-soores. If convenient, use technology to nd the zscore. P33 Click to view we 1 of the table. Click to view we 2 of the table. The z-score that corresponds to P33 is (Round to two decimal places as needed.) Use the standard normal table to nd the z-score that corresponds to the given percentile. If the area is not in the table, use the entry closest to the area. If the area is halfway between two entries, use the z-soore halfway between the corresponding z-soores. If convenient, use technology to nd the z-score. P78 Click to view page 1 of the table. Click to View p_age 2 of the table. The z-soore that corresponds to P73 is (Round to two decimal places as needed.) Find the indicated z-score shown in the graph to the right. Q Q The z-soore is . (Round '0 two decimal places as needed.) Find the indicated z-scores shown in the graph. Click to view p_age 1 of the table. Click to view p_age 2 of the table. The z-scores are . (Use a comma to separate answers as needed. Round to two decimal places as needed.) Standard Normal Table (Page 1) - 3.4 - 3.3 - 3.2 - 3.1 - 3.0 - 2.9 - 2.8 - 2.7 - 2.6 - 2.5 - 2.4 - 2.3 - 2.2 - 2.1 - 2.0 - 1.9 - 1.8 - 1.7 - 1.6 - 1.5 - 1.4 - 1.3 - 1.2 - 1.1 - 1.0 - 0.9 - 0.8 - 0.1 0.09 0.08 0.07 0.06 0.05 0.04 0.03 0.02 0.01 0.00 0.0002 0.0003 0.0003 0.0003 0.0003 0.0003 0.0003 0.0003 0.0003 0.0003 0.0003 0.0004 0.0004 0.0004 0.0004 0.0004 0.0004 0.0005 0.0005 0.0005 0.0005 0.0005 0.0005 0.0006 0.0006 0.0006 0.0006 0.0006 0.0007 0.0007 0.0007 0.0007 0.0008 0.0008 0.0008 0.0008 0.0009 0.0009 0.0009 0.0010 0.0010 0.0010 0.0011 0.0011 0.0011 0.0012 0.0012 0.0013 0.0013 0.0013 0.0014 0.0014 0.0015 0.0015 0.0016 0.0016 0.0017 0.0018 0.0018 0.0019 0.0019 0.0020 0.0021 0.0021 0.0022 0.0023 0.0023 0.0024 0.0025 0.0026 0.0026 0.0027 0.0028 0.0029 0.0030 0.0031 0.0032 0.0033 0.0034 0.0035 0.0036 0.0037 0.0038 0.0039 0.0040 0.0041 0.0043 0.0044 0.0045 0.0047 0.0048 0.0049 0.0051 0.0052 0.0054 0.0055 0.0057 0.0059 0.0060 0.0062 0.0064 0.0066 0.0068 0.0069 0.0071 0.0073 0.0075 0.0078 0.0080 0.0082 0.0084 0.0087 0.0089 0.0091 0.0094 0.0096 0.0099 0.0102 0.0104 0.0107 0.0110 0.0113 0.0116 0.0119 0.0122 0.0125 0.0129 0.0132 0.0136 0.0139 0.0143 0.0146 0.0150 0.0154 0.0158 0.0162 0.0166 0.0170 0.0174 0.0179 0.0183 0.0188 0.0192 0.0197 0.0202 0.0207 0.0212 0.0217 0.0222 0.0228 0.0233 0.0239 0.0244 0.0250 0.0256 0.0262 0.0268 0.0274 0.0281 0.0287 0.0294 0.0301 0.0307 0.0314 0.0322 0.0329 0.0336 0.0344 0.0351 0.0359 0.0367 0.0375 0.0384 0.0392 0.0401 0.0409 0.0418 0.0427 0.0436 0.0446 0.0455 0.0465 0.0475 0.0485 0.0495 0.0505 0.0516 0.0526 0.0537 0.0548 0.0559 0.0571 0.0582 0.0594 0.0606 0.0618 0.0630 0.0643 0.0655 0.0668 0.0681 0.0694 0.0708 0.0721 0.0735 0.0749 0.0764 0.0778 0.0793 0.0808 0.0823 0.0838 0.0853 0.0869 0.0885 0.0901 0.0918 0.0934 0.0951 0.0968 0.0985 0.1003 0.1020 0.1038 0.1056 0.1075 0.1093 0.1112 0.1131 0.1151 0.1170 0.1190 0.1210 0.1230 0.1251 0.1271 0.1292 0.1314 0.1335 0.1357 0.1379 0.1401 0.1423 0.1446 0.1469 0.1492 0.1515 0.1539 0.1562 0.1587 0.1611 0.1635 0.1660 0.1685 0.1711 0.1736 0.1762 0.1788 0.1814 0.1841 0.1867 0.1894 0.1922 0.1949 0.1977 0.2005 0.2033 0.2061 0.2090 0.2119 0.2148 0.2177 0.2206 0.2236 0.2266 0.2296 0.2327 0.2358 0.2389 0.2420 0.0336 0.0336 z=? 0 z=? '03 In a survey of women in a certain country (ages 20 - 29), the mean height was 65.1 inches with a standard deviation of 2.85 inches. Answer the following questions about the specified normal distribution. (a) What height represents the 95th percentile? (b) What height represents the first quartile? X Click to view page 1 of the table. Click to view page 2 of the table. Standard Normal Table (Page 2) (a) The height that represents the 95th percentile is |inches. Z 0.00 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 (Round to two decimal places as needed.) 0.0 0.5000 0.5040 0.5080 0.5120 0.5160 0.5199 0.5239 0.5279 0.5319 0.5359 0.1 0.5398 0.5438 0.5478 0.5517 0.5557 0.5596 0.5636 0.5675 0.5714 0.5753 0.2 0.5793 0.5832 0.5871 0.5910 0.5948 0.5987 0.6026 0.6064 0.6103 0.6141 0.3 0.6179 0.6217 0.6255 0.6293 0.6331 0.6368 0.6406 0.6443 0.6480 0.6517 0.4 0.6554 0.6591 0.6628 0.6664 0.6700 0.6736 0.6772 0.6808 0.6844 0.6879 0.5 0.6915 0.6950 0.6985 0.7019 0.7054 0.7088 0.7123 0.7157 0.7190 0.7224 0.6 0.7257 0.7291 0.7324 0.7357 0.7389 0.7422 0.7454 0.7486 0.7517 0.7549 0.7 0.7580 0.7611 0.7642 0.7673 0.7704 0.7734 0.7764 0.7794 0.7823 0.7852 0.8 0.7881 0.7910 0.7939 0.7967 0.7995 0.8023 0.8051 0.8078 0.8106 0.8133 0.9 0.8159 0.8186 0.8212 0.8238 0.8264 0.8289 0.8315 0.8340 0.8365 0.8389 1.0 0.8413 0.8438 0.8461 0.8485 0.8508 0.8531 0.8554 0.8577 0.8599 0.8621 1.1 0.8643 0.8665 0.8686 0.8708 0.8729 0.8749 0.8770 0.8790 0.8810 0.8830 2 0.8849 0.8869 0.8888 0.8907 0.8925 0.8944 0.8962 0.8980 0.8997 0.9015 1.3 0.9032 0.9049 0.9066 0.9082 0.9099 0.9115 0.9131 0.9147 0.9162 0.9177 1.4 0.9192 0.9207 0.9222 0.9236 0.9251 0.9265 0.9279 0.9292 0.9306 0.9319 1.5 0.9332 0.9345 0.9357 0.9370 0.9382 0.9394 0.9406 0.9418 0.9429 0.9441 1.6 0.9452 0.9463 0.9474 0.9484 0.9495 0.9505 0.9515 0.9525 0.9535 0.9545 1.7 0.9554 0.9564 0.9573 0.9582 0.9591 0.9599 0.9608 0.9616 0.9625 0.9633 1.8 0.9641 0.9649 0.9656 0.9664 0.9671 0.9678 0.9686 0.9693 0.9699 0.9706 1.9 0.9713 0.9719 0.9726 0.9732 0.9738 0.9744 0.9750 0.9756 0.9761 0.9767 2.0 0.9772 0.9778 0.9783 0.9788 0.9793 0.9798 0.9803 0.9808 0.9812 0.9817 2.1 0.9821 0.9826 0.9830 0.9834 0.9838 0.9842 0.9846 0.9850 0.9854 0.9857 2.2 0.9861 0.9864 0.9868 0.9871 0.9875 0.9878 0.9881 0.9884 0.9887 0.9890 2.3 0.9893 0.9896 0.9898 0.9901 0.9904 0.9906 0.9909 0.9911 0.9913 0.9916 2.4 0.9918 0.9920 0.9922 0.9925 0.9927 0.9929 0.9931 0.9932 0.9934 0.9936 2.5 0.9938 0.9940 0.9941 0.9943 0.9945 0.9946 0.9948 0.9949 0.9951 0.9952 2.6 0.9953 0.9955 0.9956 0.9957 0.9959 0.9960 0.9961 0.9962 0.9963 0.9964 2.7 0.9965 0.9966 0.9967 0.9968 0.9969 0.9970 0.9971 0.9972 0.9973 0.9974The per capita energy consumption level (in kilowatt-hours) in a certain country for a recent year can be approximated by a normal distribution, as shown in the figure. (a) What consumption level represents the 9th percentile? (b) What consumption level represents the 24th percentile? (c) What consumption level represents the third quartile? H = 2312 kWh OF 587.4 KWh 312 2312 4312 Kilowatt-hours . . . . . (a) The consumption level that represents the 9th percentile is kilowatt-hours. (Round to the nearest integer as needed.)The undergraduate grade point averages (UGPA) of students taking an admissions test in a recent year can be approximated by a normal distribution, as shown in the gure. 0' (a) What is the minimum UGPAthat would still place a student in the top 15% of UGPAs'? (b) Between what two values does the middle 50% of the UGPAs lie? ll 3 32 Q o 0.1 13' X 2.64 3.32 4 Grade point average (a) The minimum UGPA that would still place a student in the top 15% of UGPAs is (Round to two decimal places as needed.) The test scores for the analytical writing section of a particular standardized test can be approximated by a normal distribution, as shown in the figure. (a) What is the maximum score that can be in the bottom 10% of scores? (b) Between what two values does the middle 80% of scores lie? H = 3. OF 0.81 X 0.6 3.3 6 Score . . . . . (a) The maximum score that can be in the bottom 10% is. (Round to two decimal places as needed.)A population has a mean p.= 74 and a standard deviation 6 = 18. Find the mean and standard deviation of a sampling distribution of sample means with sample size n = 36. ..... \"i = I: (Simplify your answer.) Determine whether the statement is true or false. If it is false, rewrite it as a true statement. As the size of a sample increases, the mean of the distribution of sample means increases. Choose the correct answer below. 0 A. True. 0 B. False. As the size of a sample increases, the mean of the distribution of sample means decreases. O C. False. As the size of a sample increases, the mean of the distribution of sample means does not change. Determine whether the statement is true or false. If it is false, rewrite it as a true statement. A sampling distribution is normal only if the population is normal. Choose the correct answer below. 0 A. The statement is true. 0 B. The statement is false. A sampling distribution is normal only if n 2 30. O c. The statement is false. A sampling distribution is never normal. 0 D. The statement is false. A sampling distribution is normal if either n 2 30 or the population is normal. Determine whether the statement is true or false. If it is false, rewrite it as a true statement. If the size of a sample is at least 30, then you can use z-soores to determine the probability that a sample mean falls in a given interval of the sampling distribution. Choose the correct choice below. 0 A. This statement is false. A true statement is, "If the size of a sample is at least 50, then you can use zsoores to determine the probability that a sample mean falls in a given interval of the sampling distribution." 0 B. This statement is false. A true statement is, "If the size of a sample is at least 10, then you can use z-scores to determine the probability that a sample mean falls in a given interval of the sampling distribution." 0 c. This statement is true. O D. This statement is false. A true statement is, "There is not any size of a sample that allows you to use zscores to determine the probability that a sample mean falls in a given interval of the sampling distribution." The population mean and standard deviation are given below. Find the required probability and determine whether the given sample mean would be considered unusual. For a sample of n = 67, find the probability of a sample mean being less than 24.6 if u = 25 and 6 =1.3. E Click the icon to view page 1 of the standard normal table. a Click the icon to view page 2 of the standard normal table. For a sample of n = 67, the probability of a sample mean being less than 24.6 if u = 25 and o = 1.3 is D. (Round to four decimal places as needed.) The population mean and standard deviation are given below. Find the indicated probability and determine whether a sample mean in the given range below would be oonsidered unusual. If convenient, use technology to find the probability. For a sample of n = 35, find the probability of a sample mean being less than 12,750 or greater than 12,753 when u = 12,750 and a = 1.3. For the given sample, the probability of a sample mean being less than 12,750 or greater than 12,753 is (Round to four decimal places as needed.) Find the probability and interpret the results. If convenient, use technology to nd the probability. The population mean annual salary for environmental compliance specialists is about $61,500. A random sample of 40 specialists is drawn from this population. What is the probability that the mean salary of the sample is less than $59,500? Assume a = $5,500. The probability that the mean salary of the sample is less than $59,500 is (Round to four decimal places as needed.) A machine used to ll gallon-sized paint cans is regulated so that the amount of paint dispensed has a mean of 124 ounces and a standard deviation of 0.20 ounoe. You randomly select 40 cans and carefully measure the contents. The sample mean of the cans is 123.9 ounces. Does the machine need to be reset? Explain your reasoning. 'V , it is 1 that you would have randomly sampled 40 cans with a mean equal to 123.9 ounces, because it 7 within the range of a usual event, namely within : of the mean of the sample means. The average math SAT score is 521 with a standard deviation of 113. A particular high school claims that its students have unusually high math SAT scores. A random sample of 55 students from this school was selected, and the mean math SAT score was 538. Is the high school justied in its claim? Explain. l: , because the z-score( ) is V since it V within the range ofa usual event, namely within : of the mean of the sample means. (Round to two decimal places as needed.) The lengths of lumber a machine cuts are normally distributed with a mean of 92 inches and a standard deviation of 0.5 inch. (a) What is the probability that a randomly selected board cut by the machine has a length greater than 92.17 inches? (b) A sample of 44 boards is randomly selected. What is the probability that their mean length is greater than 92.17 inches? (a) The probability is E. (Round to four decimal places as needed.) The weights of ice cream cartons are normally distributed with a mean weight of 9 ounces and a standard deviation of 0.5 ounce. (a) What is the probability that a randomly selected carton has a weight greater than 9.14 ounces? (b) A sample of 25 cartons is randomly selected. What is the probability that their mean weight is greater than 9.14 ounces? (a) The probability is D. (Round to four decimal places as needed.) Determine if the finite correction factor should be used. If so, use it in your calculations when you find the probability. In a sample of 700 gas stations, the mean price for regular gasoline at the pump was $2.835 per gallon and the standard deviation was $0.008 per gallon. A random sample of size 60 is drawn from this population. What is the probability that the mean price per gallon is less than $2.832? The probability that the mean price per gallon is less than $2.832 is. (Round to four decimal places as needed.)Find the probability and interpret the results. If convenient, use technology to nd the probability. The population mean annual salary for environmental compliance specialists is about $63,000. A random sample of 34 specialists is drawn from this population. What is the probability that the mean salary of the sample is less than $61,000? Assume a = $5,600. The probability that the mean salary of the sample is less than $61,000 is (Round to four decimal places as needed.) 1 1 point A random variable x is normally distributed with a mean of 117 and a standard deviation of 14. What is the probability of selecting any random variable from the distribution with a value less than 112? Provide your answer as a percentage to two decimal places. type your answer... 2 1 point A random variable x is normally distributed with a mean of 117 and a standard deviation of 14. P(X s 124)? Provide your answer as a percentage to two decimal places. type your answer... 3 1 point A random variable x is normally distributed with a mean of 117 and a standard deviation of 14. P(X 2 145 )? Provide your answer as a percentage to two decimal places. type your answer...3 points Q The SAT Math scores from 2019 are normally distributed with a mean of 528 and a standard deviation of 117. What is the probability of randomly selecting a test score that is a) less than 495 type your answer... 1 b) between 515 and 690 type your answer... c) greater than 670 type your answer... Provide probabilities rounded to the third decimal place or percentage rounded to the rst decimal place. Source: The College Board 3 points 9 The SAT scores from 2019 are normally distributed with a mean of 1059 and a standard deviation of 210. What is percentage of scores are a) greater than 1200 type your answer... ' b) between 1000 and 1100 type your answer... c) less than 800 type your answer... ' Express all answers as percentage to two decimal places. Source: The College Board a 1 point 9 If the mean of a normal distribution is 45 and the standard deviation is 4.3, how many standard deviations away from the mean is the value 36.8? Write your z-score as a negative or positive number with two decimal places. type your answer... 2 points Calculate the standard error for each of the following problems. Round all answers to four decimal places: a) u = 23.7; o = 4.5; n = 30 type your answer... b) u = 1272.5; 0 = 145.2; n = 100 J type your answer... c) u = 845.9; 0 = 46.8; n = 60 type your answer... J d) u = .024; o = .003; n = 45 J type your answer... J 4 points Calculate the probabilities for each of the following problems. Round all answers to four decimal places: a) For a distribution with u = 23.7; o = 4.5; n = 30, what is the probability of randomly selecting a value less than 22? J type your answer... J b) For a distribution with p = 1272.5; 0 = 145.2; n = 100, what is the probability of randomly selecting a value more than 1290? J type your answer... J c) For a distribution with u = 845.9; a = 46.8; n = 60, what is the probability of randomly selecting a value less than 835? type your answer... d) For a distribution with p = .024; o = .003; n = 45, what is the probability of randomly selecting a value more than .025? J type your answer... J In Question 2, which of those events are signicant? b) d) C) a) 1 point In order to satisfy the Central Limit Theorem, what conditions must be met? Select all that apply. GOOD The population must have a normal distribution The sample size (n) must be at least 30 The sample size (n) must be greater than 1 The population may have any distribution shape, but the sample population must be normal The sample size (n) must represent 5% or more of the population DODCJCJCJ It does not matter what shape the population distribution has because the sampling distribution of the sample means will be normally distributed 1 point For sampling distributions of a sample statistic, select all of the following statements which are true: The mean of the sampling distribution is the mean of the population divided by the sample size (n) The standard deviation of the sampling distribution is the same as the population standard deviation The standard deviation of the sampling distribution can be found by diving the population variance by the sample size (n) and then taking the square root of that value The standard deviation of the sampling distribution is the standard deviation of the population divided by the sample size (n) We do not use the standard deviation of the population, instead we use the standard error The mean of the sampling distribution is the same as the mean of the population CJCJDCJDDD The standard deviation of the sampling distribution is the standard deviation of the population divided by the square root of the sample size (n) 1 point For sampling distributions of a sample statistic, select all of the following statements which are true: The mean of the sampling distribution is the mean ofthe population divided by the sample size (n) The standard deviation of the sampling distribution is the same as the population standard deviation The standard deviation of the sampling distribution can be found by diving the population variance by the sample size (n) and then taking the square root of that value The standard deviation of the sampling distribution is the standard deviation of the population divided by the sample size (n) We do not use the standard deviation of the population, instead we use the standard error The mean of the sampling distribution is the same as the mean of the population CJCJCJCJCJOD The standard deviation of the sampling distribution is the standard deviation of the population divided by the square root of the sample size (n) Increasing the sample size (n), has the following effect on the sampling distribution: The greater the sample size (n), the smaller the standard error of the sampling distribution The greater the sample size (n), the smaller the standard deviation of the sampling distribution The greater the sample size (n), smaller the data spread of the sampling distribution OBOE] The greater the sample size (n), the closer the average of the sample statistic will be to the population parameter