Answered step by step
Verified Expert Solution
Question
1 Approved Answer
ate 61'10 Approximate all points of relative and absolute extrema of each function. Then approximate the open intervals where each function is increasing and decreasing.
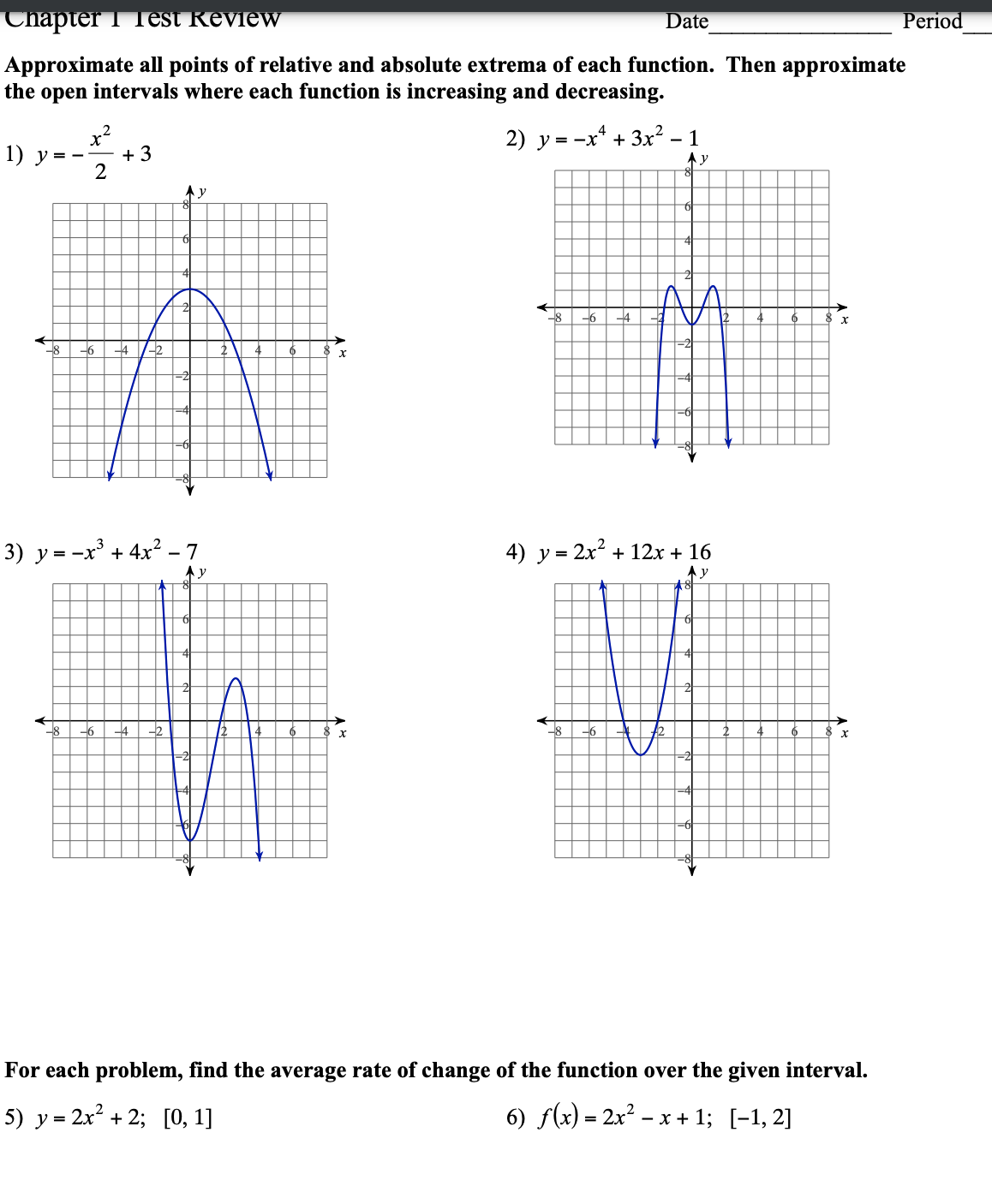
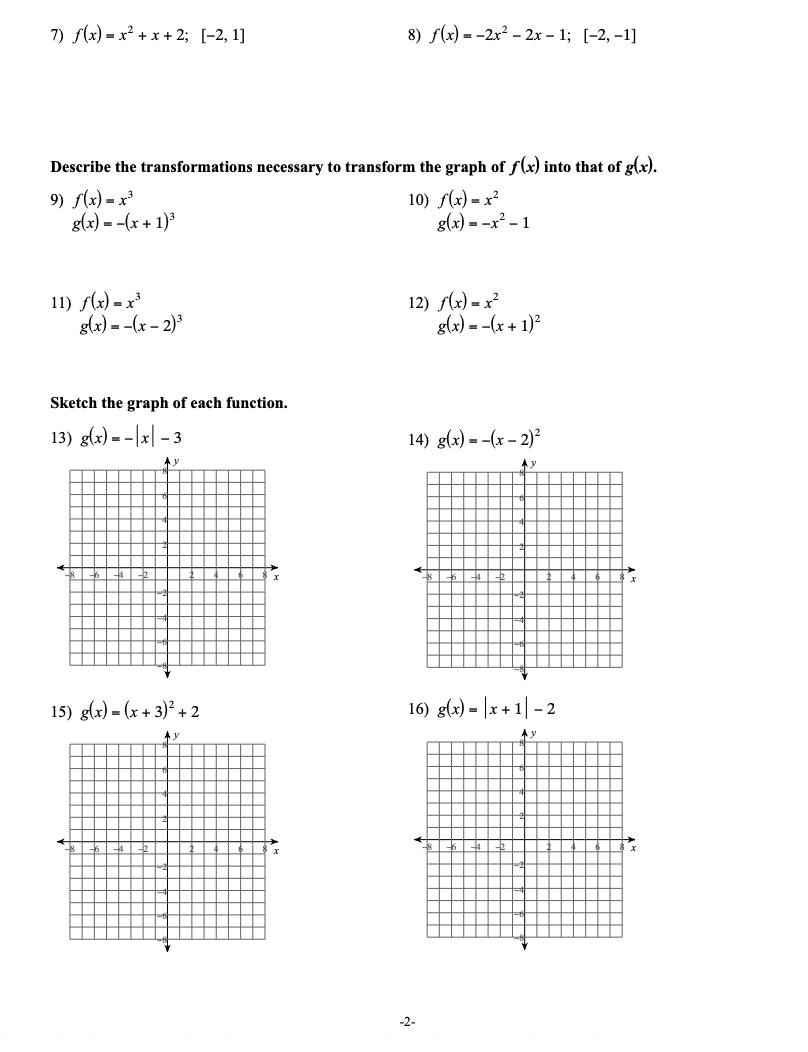

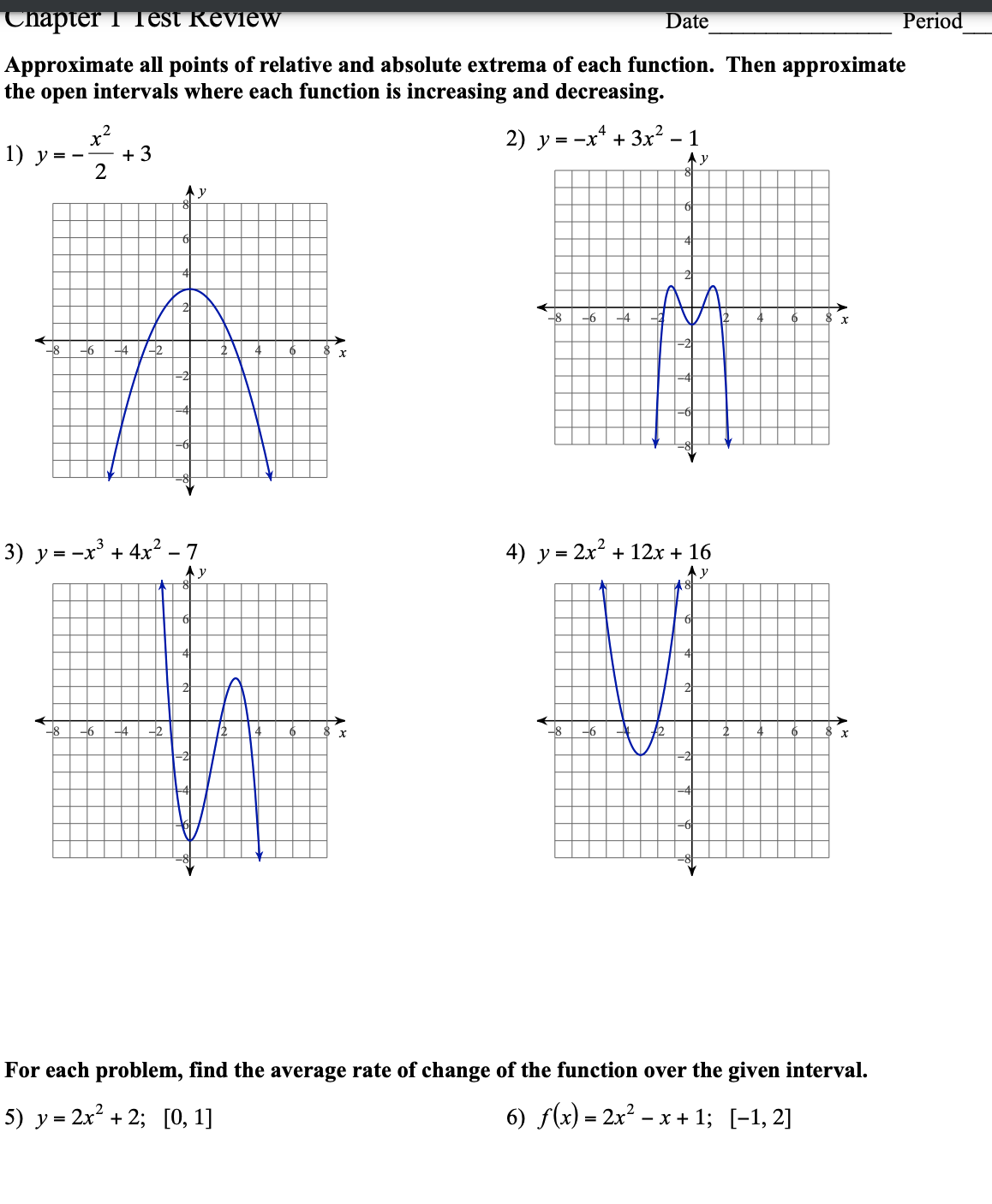
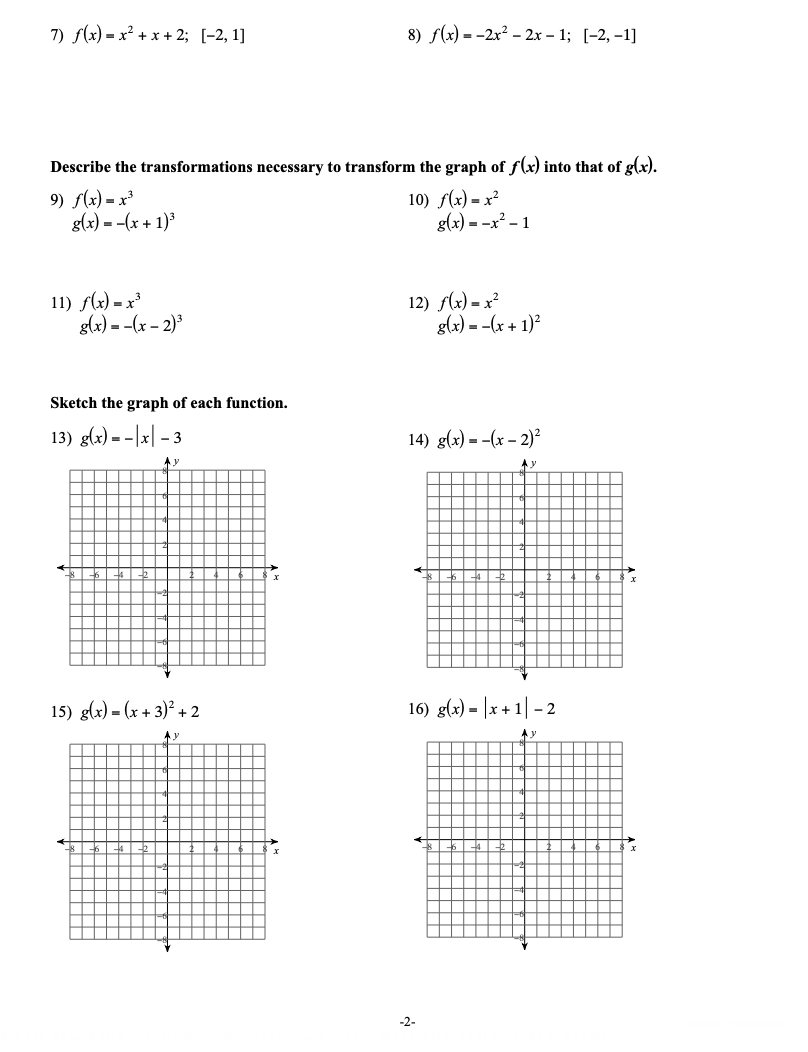

Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


