Autocorrelation of a sinusoidal signal plus white Gaussian noise

Make a matlab code for the following project, the graphs should be as shown below

In this project, the statistical characterization of a stochastic process that consists of a sinusoidal signal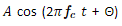 and a Gaussian white noise process () of zero mean and power spectral density 0/2 will be studied. That is, we have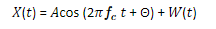

where is a random variable uniformly distributed over the interval. The autocorrelation function of () is therefore the sum of the individual autocorrelation functions.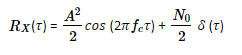

The purpose of the project is to perform this calculation using the joint average. The following figure shows a sinusoidal signal with frequency fc=0.002 Hz, fase = [ , ], truncated to a finite duration = 1000 seconds; The amplitude A of the sinusoidal signal is set to 2 to give the unit average energy. The noise power spectral density for this embodiment is N0/2=1

For the ensemble-averaged calculation of the autocorrelation function, we can proceed as follows:

Compute the product ( + ) () for a fixed time and a specific time shift , where () is a particular realization of the random process ().

Repeat the calculation of the product ( + ) () for M independent realizations (i.e., sample functions) of the random process ().

Calculate the average of these calculations over = 500.

Repeat this sequence of calculations for different values of .

Acos(2fct+) X(t)=Acos(2fct+)+W(t) RX()=2A2cos(2fc)+2N0() mM