Automatas and Languages with Python!

Build a NonDeterminsiticAutomaton class in Python. Your class should have the following methods:

• initialize(q, sigma, delta, q0, f, empty symbol): this method receives the non-deterministic automaton elements and set its own properties
• load_from_file(path): this method receives the file with the automaton definition and loads the properties (see attached files example)
• process_symbol(state, symbol): this method receives a string representing the state and the symbol to process and returns the set of possible next states
• empty_transitions(state): this method receives a string representing the state and returns the set of possible states reachable using empty transitions from that state.
• process_word(word): this method receives a string and return a Boolean indicating if the string is accepted or not. It also should print the transitions chosen to reach a final state incase that the word is accepted.
• __str__: prints current automaton configuration (including current state)
• is_valid(q, sigma, delta, q0, f): this method receives the automaton elements and returns a Boolean indicating if it is a valid automaton definition.

I already have all the methods except by the process_word method. You can find the python code and the files to test it in this link: https://drive.google.com/drive/folders/1u7mT79MYMZo3eXDFJzXHA83xGKXu2g-3?usp=sharing.

It is a google drive folder where a colaboratory file (jupyter notebook from Google) and a folder with txt files to test the code can be found.

I already have a process_word function, however, it does not meet the definition of word processing of a NFA.

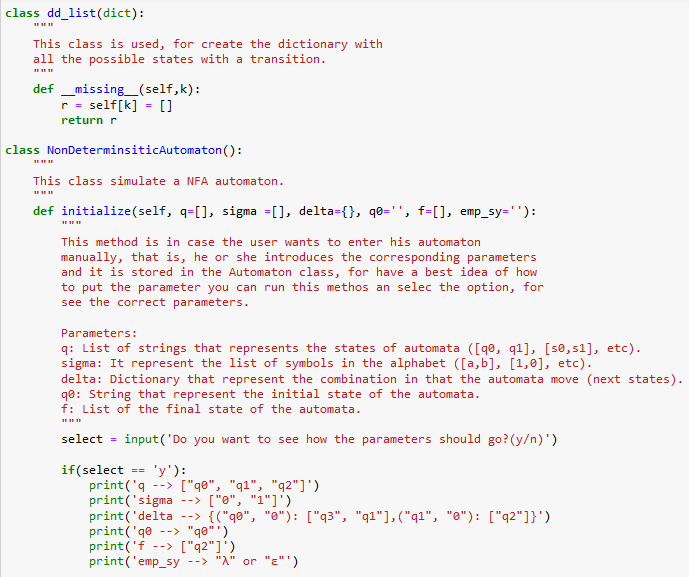
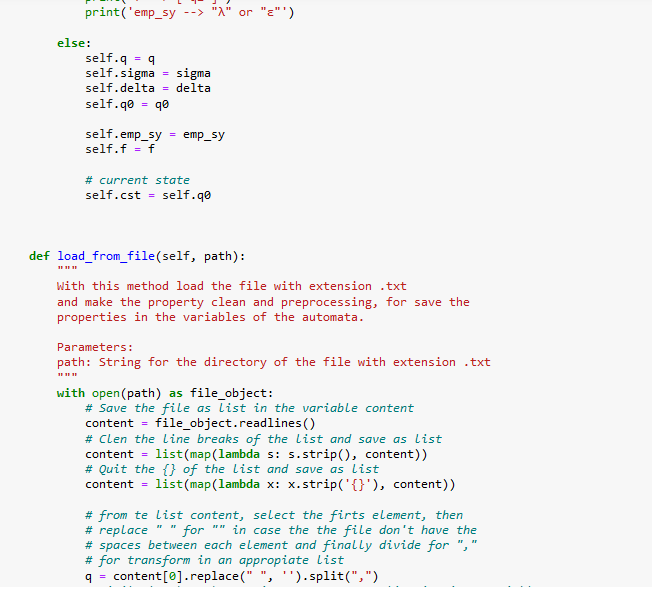
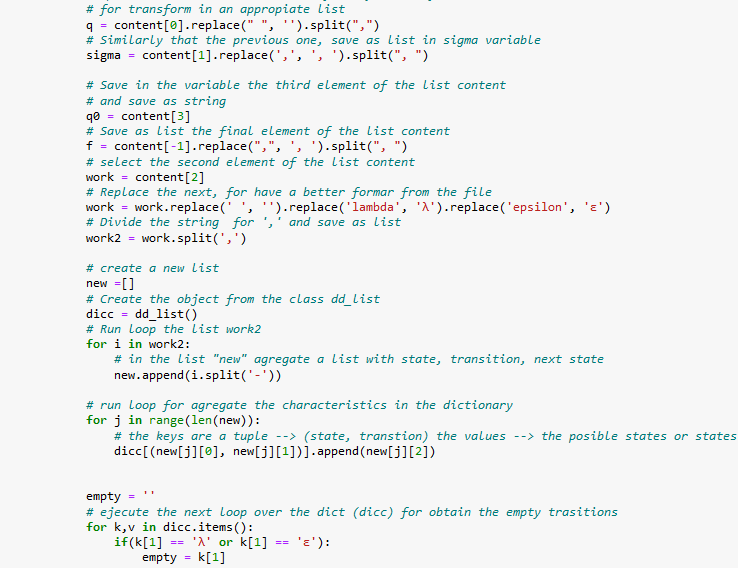
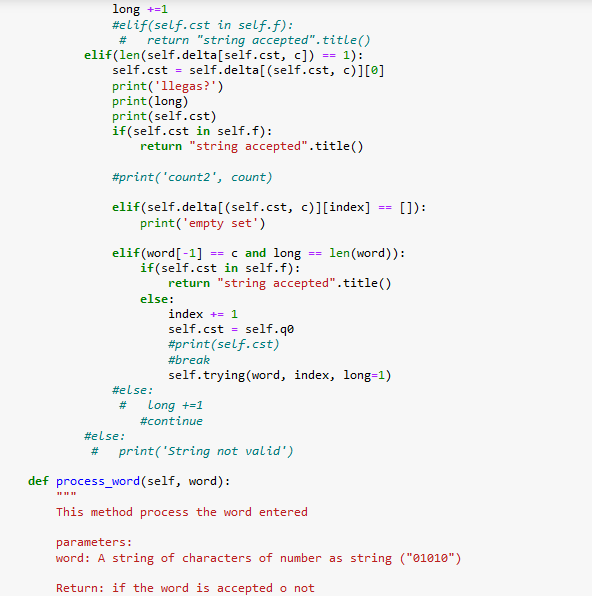
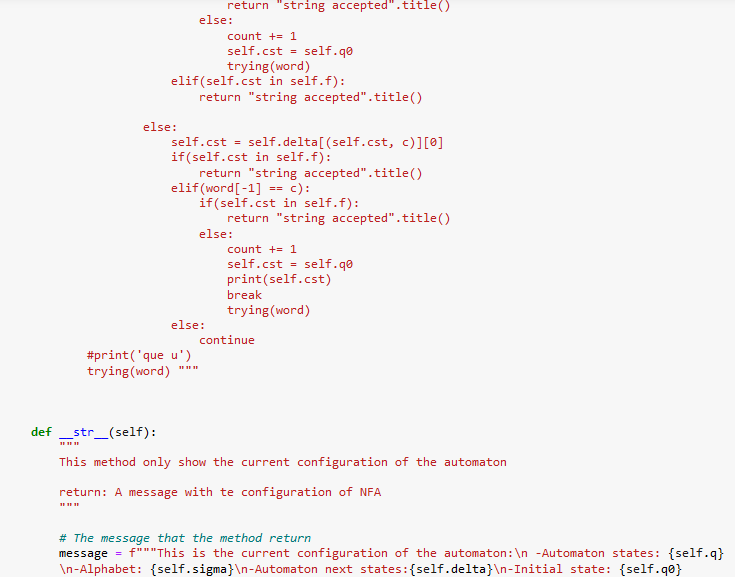
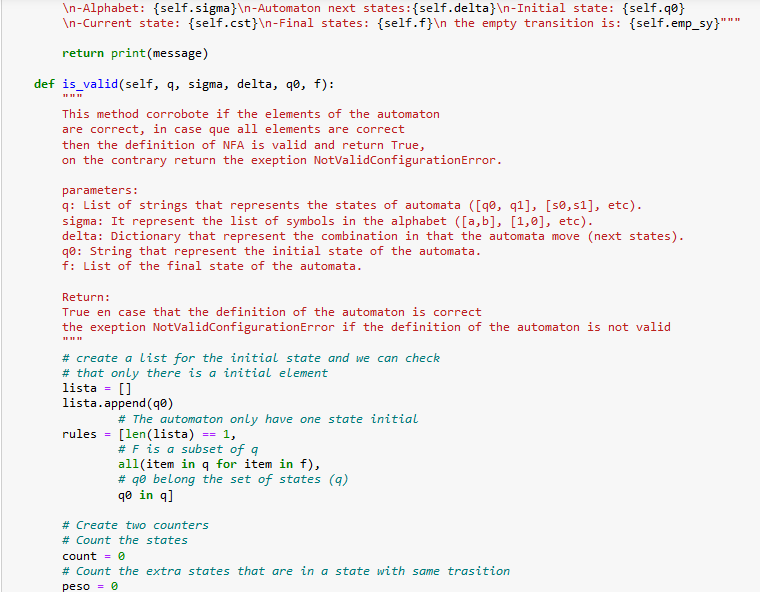
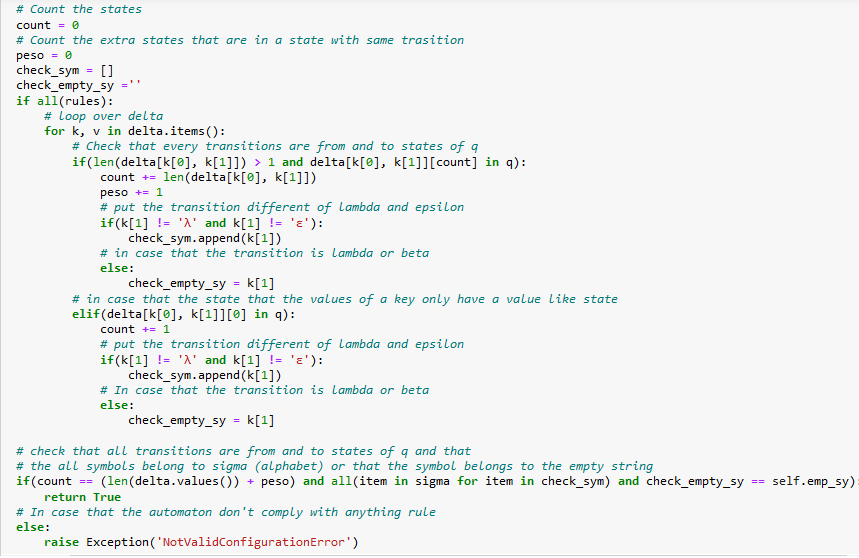
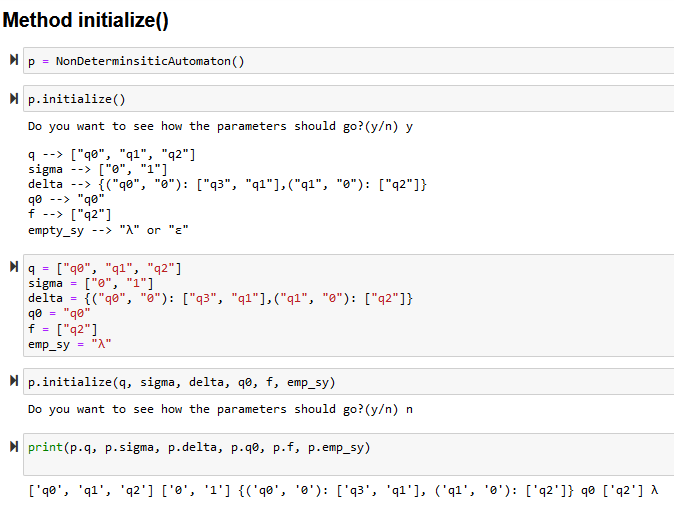
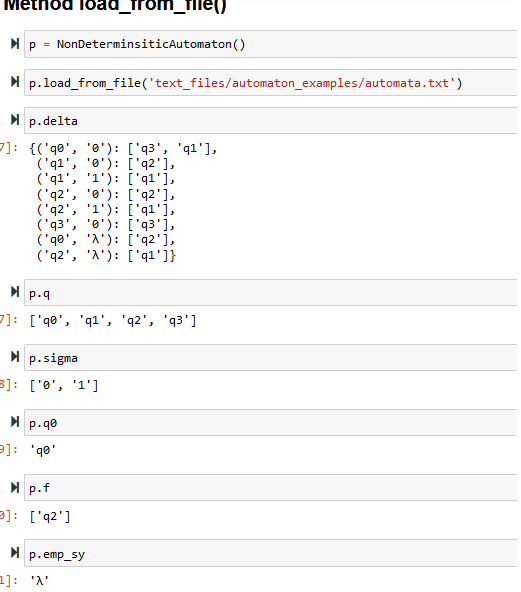
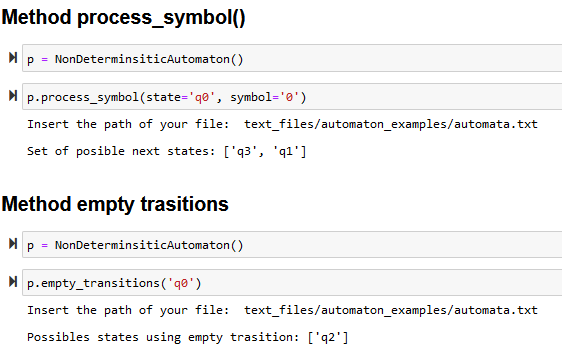
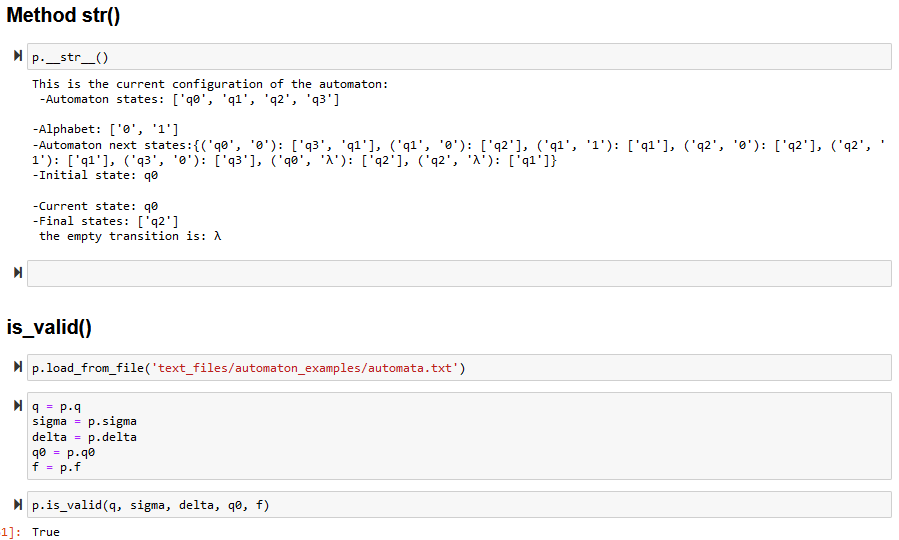
I'm uploading code images just in case. I am using jupyter notebook but of course you can run the code in any other IDE. If there's any question please let me know. I know there's a lot picture of code but there's little of work for this only. Thanks in advance!!!

class dd_list(dict): This class is used, for create the dictionary with all the possible states with a transition. def _missing_(self,k): r = self[k] = [] return r class NonDeterminsiticAutomaton) : This class simulate a NFA automaton. def initialize(self, q=[], sigma = [], delta={}, qo=", f=[], emp_sy=''): This method is in case the user wants to enter his automaton manually, that is, he or she introduces the corresponding parameters and it is stored in the Automaton class, for have a best idea of how to put the parameter you can run this methos an selec the option, for see the correct parameters. Parameters: q: List of strings that represents the states of automata ([90, 91], [50,51], etc). sigma: It represent the list of symbols in the alphabet ([a,b], [1,0], etc). delta: Dictionary that represent the combination in that the automata move (next states). 90: String that represent the initial state of the automata. f: List of the final state of the automata. select = input('Do you want to see how the parameters should go? (y)') if(select 'y'): print('q. --> ["90", "q1", "q2"]') print('sigma --> ["0", "1"]') print('delta --> {("90", "6"): ["93", "91"],("71", ""): ["q2"]}') print('90 --> "90"') print('f --> ["q2"]') print('emp_sy --> "X" or ""') print('emp_sy --> "" or " (state, transtion) the values --> the posible states or states dicc[(new[j][@], new[j][1])].append(new[j][2]) empty = # ejecute the next loop over the dict (dicc) for obtain the empty trasitions for k,v in dicc.items(): if(k[1] 'X' or k[1] ''): empty = k[1] == == empty k[1] # Finally of process all correctly save in the parameters of the class self.q = 9 self.sigma sigma self.delta dicc self.90 90 self.f - f self.cst 90 #self.90 self.emp_sy empty def process_symbol(self, state, symbol): With this method load the state and the symbol as string and returns the set of possibles next states parameter: State: String --> qo symbol: String --> 0 # Replace the states that are Lambda and epsilon for their sign symbol symbol.replace('lambda', '').replace('epsilon', 'a') # Create the list (state, transition] #sy = symbol.split('-) # select the state #state = sy[@] # Select the transition or symbol #symbol sy[1] # Is necessary put the file of the automaton path = input('Insert the path of your file: ') # Call the method Load_from_file self.load_from_file(path) # Create a condition for check if the state and transition are valid if((state, symbol) in self.delta): # Loop over the dictionary (dicc) for k,v in self.delta.items(): # Loop over the dictionary (dicc) for k,v in self.delta.items(): # If the transition is equal to the symbol, print the posible states if(k[1] == symbol): return print(f'Set of posible next states: {v}') # In other case is not valid the state and transition else: print('Not valid') def empty_transitions(self, state): This method receive a string, a state of the automaton, and return the possible states using empty trasitions Parameters: state: A string representing the state of the automaton as 90, 91, etc. 11 # insert the path path input('Insert the path of your file: ') # Call the method Load_from_file self.load_from_file(path) # the state has empty transitions (Lamdba) if((state, 'X') in self.delta): # Loop over the delta (dicc) for k, v in self.delta.items(): # If the state has empty trasitions print the reachable states if(k[@] == state and k[1] == 'X'): # Return the possible states return print(f'Possibles states using empty trasition: {v}') # If the state has epsilon as empty transition elif((state, 'a') in self.delta): # Loop over the delta (dicc) for k, v in self.delta.items(): #If the state has empty trasitions print the reachable states with epsilon if(k[o] state and k[1] ''): == # Return the possibles states return print(f'Possibles states using empty trasition: {v}') # In case that the state don't have any empty transition else: return 'Not valid' def trying(self, word, index = 0, long=1): This method tyr to make a recursion for process the word :( but we have problems, first the depth of the recursion was very heavy, then we have problemas with the index :( #count += @ #print('que u') #print('iniciando') #count = @ for c in word: #for k,v in self.delta.items(): #print(Len(self.delta[self.cst, c]), count) if(len(self.delta[self.cst, c]) > 1): self.cst = self.delta[(self.cst, c)][index] print('primera: ', self.cst) print('index', index) print('long:', long) print('word: ', c) #count = 0 #if(self.delta[(self.cst, c)][index] []): print('empty set') == # if(word[-1] == c and long len (word)): if(self.cst in self.f): return "string accepted".title() else: #count += 1 self.cst = self.90 self.trying(word, index, long=1) long += 1 # 1): long +=1 #elif(self.cst in self.f): return "string accepted".title) elif(len(self.delta[self.cst, c]) == self.cst = self.delta[(self.cst, c)][0] print('llegas?') print(long) print(self.cst) if(self.cst in self.f): return "string accepted".title) #print('count2', count) elif(self.delta[(self.cst, c)][index] == []): print('empty set') elif(word[-1] == c and long == len(word)): if(self.cst in self.f): return "string accepted".title) else: index += 1 self.cst = self.90 #print(self.cst) #break self.trying(word, index, long=1) #else: Long +=1 #continue #else: print('String not valid') # # def process_word(self, word): This method process the word entered parameters: word: A string of characters of number as string ("01010") Return: if the word is accepted o not Return: if the word is accepted o not path input('Insert your file with extension .txt: ') self.load_from_file(path) # Convert the word in strig in case that the user insert # numbers word = str(word) # change the spaces for empty string word.replace("'', '').replace('lambda', 'x').replace('epsilon', 'a') #if the word isn't in the alphabet the word isn't not accepted if(word[C] not in self.sigma): return 'Empty set' else: self.trying(word) # In this part we intend to solve for process the word # with a different approach, but we have a lot of problems count = 0 def trying (word, count=0): count += 0 #print('que u') #print('iniciando') #count = 0 for c in word: #for k,v in self.delta.items(): if(len(self.delta[self.cst, c]) > 1): self.cst = self.delta[(self.cst, c)][count] #count += 1 #if(self.delta[(self.cst, c)][count] == []): # print('empty set') if(word [-1] c): if(self.cst in self.f): return "string accepted".title) == return "string accepted".title) else: count += 1 self.cst = self.90 trying (word) elif(self.cst in self.f): return "string accepted".title) else: self.cst = self.delta[(self.cst, c)][0] if(self.cst in self.f): return "string accepted".title) elif (word[-1] == c): if(self.cst in self.f): return "string accepted".title) else: count += 1 self.cst = self.qo print(self.cst) break trying(word) else: continue #print('que u') trying (word) def str_(self): This method only show the current configuration of the automaton return: A message with te configuration of NFA # The message that the method return message = f"*"This is the current configuration of the automaton: -Automaton states: {self.q} -Alphabet: {self.sigma} -Automaton next states:{self.delta} -Initial state: {self.90} -Alphabet: {self.sigma} -Automaton next states:{self.delta} -Initial state: {self.90} -Current state: {self.cst} -Final states: {self.f} the empty transition is: {self.emp_sy}"*" return print(message) def is_valid(self, q, sigma, delta, 90, f): This method corrobote if the elements of the automaton are correct, in case que all elements are correct then the definition of NFA is valid and return True, on the contrary return the exeption NotValidConfigurationError. parameters: q: List of strings that represents the states of automata ([90, 91], [50, 51], etc). sigma: It represent the list of symbols in the alphabet ([a,b], [1,0], etc). delta: Dictionary that represent the combination in that the automata move (next states). 20: String that represent the initial state of the automata. f: List of the final state of the automata. Return: True en case that the definition of the automaton is correct the exeption NotValidConfigurationError if the definition of the automaton is not valid # create a list for the initial state and we can check # that only there is a initial element lista = [] lista.append(90) # The automaton only have one state initial rules = [len(lista) == 1, # F is a subset of a all(item in q for item in f), # qe belong the set of states (9) qo in q] # Create two counters # Count the states count = 0 # Count the extra states that are in a state with same trasition peso = 6 # Count the states count = 0 # Count the extra states that are in a state with same trasition peso = 0 check_sym [] check_empty_sy=" if all(rules): # Loop over delta for k, v in delta.items(): # Check that every transitions are from and to states of a if(len(delta[k[@], k[1]]) > 1 and delta[k[@], k[1]][count] in q): count += len(delta[k[@], k[1]]) peso += 1 # put the transition different of Lambda and epsilon if(k[1] != 'X' and k[1] != 'a'): check_sym.append(k[1]) # in case that the transition is Lambda or beta else: check_empty_sy = K[1] # in case that the state that the values of a key only have a value like state elif(delta[k[@], k[1]][C] in q): count += 1 # put the transition different of Lambda and epsilon if(k[1] != 'X' and k[1] != 'a'): check_sym.append(k[1]) # In case that the transition is Lambda or beta else: check_empty_sy = k[1] # check that all transitions are from and to states of q and that # the all symbols belong to sigma (alphabet) or that the symbol belongs to the empty string if(count == (len(delta.values() + peso) and all(item in sigma for item in check_sym) and check_empty_sy return True # In case that the automaton don't comply with anything rule else: raise Exception('NotValidConfigurationError') == self.emp_sy) Method initialize() p = NonDeterminsiticAutomaton() p.initialize() Do you want to see how the parameters should go? (y) y 9 --> ["90", "q1", "q2"] sigma --> ["0", "1"] delta --> {("90", "o"): ["93", "q1"],("91", "6"): ["42"]} 90 --> "90" f --> ["42"] empty_sy --> "X" or "2" N 9 ["90", "q1", "2"] sigma ["0", "1"] delta {("90", "o"): ["93", "q1"],("91", "o"): ["92"]} 90 = "90" f = ["q2"] emp_sy = "X" p.initialize(q, sigma, delta, q0, f, emp_sy) Do you want to see how the parameters should go? (y) n print(p.q, p.sigma, p.delta, p.q0, p.f, p.emp_sy) ['qo', 'qi', 'q2'] ['0', '1'] {('qo', '0'): ['q3', 'q1'), ('qi', '0'): ['q2']} 90 ('92'] , Method load p = NonDeterminsiticAutomaton) p.load_from_file('text_files/automaton_examples/automata.txt') p.delta 7]: {('90', '0'): ['93', 'q1'], ('qi', '0'): ['q2'], ('qi', '1'): ['q1'], ('92', '0'): ('92'], ('92', '1'): ['qi'], ('93', '0'): ['q3'], ('q8', 'A'): ['12'], ('92', 'X): ['qi']} p.9 7]: ['qo', 'qi', 'q2', 'q3'] Np.sigma B]: ['e', '1'] p.90 ]: 'qo' p.f ]: ['92'] p.emp_sy 1]: x Method process_symbol() p = NonDeterminsiticAutomaton() p.process_symbol(state='qo', symbol='0') Insert the path of your file: text_files/automaton_examples/automata.txt Set of posible next states: ['93', '41'] Method empty trasitions p = NonDeterminsiticAutomaton) p.empty_transitions('90') Insert the path of your file: text_files/automaton_examples/automata.txt Possibles states using empty trasition: ('92'] Method str() p._str_) This is the current configuration of the automaton: -Automaton states: ['qo', 'q1', 'q2', 'q'] -Alphabet: ['o', '1'] -Automaton next states:{('90', '0'): ['93', '41'], ('91', '0'): ['92'], ('91', '1'): ['91'], ('92', '0'): ['92'], ('92', 1'): ['q1'], ('93', '0'): ['93'), ('90', ''): ['92'], ('92', 'X'): ['q1']} -Initial state: 90 -Current state: 90 -Final states: ['92'] the empty transition is: X is_valido) p.load_from_file('text_files/automaton_examples/automata.txt') Na - p.4 sigma p.sigma delta p.delta 90 = p.90 f = p.f Np.is_valid(q, sigma, delta, 90, f) 1]: True class dd_list(dict): This class is used, for create the dictionary with all the possible states with a transition. def _missing_(self,k): r = self[k] = [] return r class NonDeterminsiticAutomaton) : This class simulate a NFA automaton. def initialize(self, q=[], sigma = [], delta={}, qo=", f=[], emp_sy=''): This method is in case the user wants to enter his automaton manually, that is, he or she introduces the corresponding parameters and it is stored in the Automaton class, for have a best idea of how to put the parameter you can run this methos an selec the option, for see the correct parameters. Parameters: q: List of strings that represents the states of automata ([90, 91], [50,51], etc). sigma: It represent the list of symbols in the alphabet ([a,b], [1,0], etc). delta: Dictionary that represent the combination in that the automata move (next states). 90: String that represent the initial state of the automata. f: List of the final state of the automata. select = input('Do you want to see how the parameters should go? (y)') if(select 'y'): print('q. --> ["90", "q1", "q2"]') print('sigma --> ["0", "1"]') print('delta --> {("90", "6"): ["93", "91"],("71", ""): ["q2"]}') print('90 --> "90"') print('f --> ["q2"]') print('emp_sy --> "X" or ""') print('emp_sy --> "" or " (state, transtion) the values --> the posible states or states dicc[(new[j][@], new[j][1])].append(new[j][2]) empty = # ejecute the next loop over the dict (dicc) for obtain the empty trasitions for k,v in dicc.items(): if(k[1] 'X' or k[1] ''): empty = k[1] == == empty k[1] # Finally of process all correctly save in the parameters of the class self.q = 9 self.sigma sigma self.delta dicc self.90 90 self.f - f self.cst 90 #self.90 self.emp_sy empty def process_symbol(self, state, symbol): With this method load the state and the symbol as string and returns the set of possibles next states parameter: State: String --> qo symbol: String --> 0 # Replace the states that are Lambda and epsilon for their sign symbol symbol.replace('lambda', '').replace('epsilon', 'a') # Create the list (state, transition] #sy = symbol.split('-) # select the state #state = sy[@] # Select the transition or symbol #symbol sy[1] # Is necessary put the file of the automaton path = input('Insert the path of your file: ') # Call the method Load_from_file self.load_from_file(path) # Create a condition for check if the state and transition are valid if((state, symbol) in self.delta): # Loop over the dictionary (dicc) for k,v in self.delta.items(): # Loop over the dictionary (dicc) for k,v in self.delta.items(): # If the transition is equal to the symbol, print the posible states if(k[1] == symbol): return print(f'Set of posible next states: {v}') # In other case is not valid the state and transition else: print('Not valid') def empty_transitions(self, state): This method receive a string, a state of the automaton, and return the possible states using empty trasitions Parameters: state: A string representing the state of the automaton as 90, 91, etc. 11 # insert the path path input('Insert the path of your file: ') # Call the method Load_from_file self.load_from_file(path) # the state has empty transitions (Lamdba) if((state, 'X') in self.delta): # Loop over the delta (dicc) for k, v in self.delta.items(): # If the state has empty trasitions print the reachable states if(k[@] == state and k[1] == 'X'): # Return the possible states return print(f'Possibles states using empty trasition: {v}') # If the state has epsilon as empty transition elif((state, 'a') in self.delta): # Loop over the delta (dicc) for k, v in self.delta.items(): #If the state has empty trasitions print the reachable states with epsilon if(k[o] state and k[1] ''): == # Return the possibles states return print(f'Possibles states using empty trasition: {v}') # In case that the state don't have any empty transition else: return 'Not valid' def trying(self, word, index = 0, long=1): This method tyr to make a recursion for process the word :( but we have problems, first the depth of the recursion was very heavy, then we have problemas with the index :( #count += @ #print('que u') #print('iniciando') #count = @ for c in word: #for k,v in self.delta.items(): #print(Len(self.delta[self.cst, c]), count) if(len(self.delta[self.cst, c]) > 1): self.cst = self.delta[(self.cst, c)][index] print('primera: ', self.cst) print('index', index) print('long:', long) print('word: ', c) #count = 0 #if(self.delta[(self.cst, c)][index] []): print('empty set') == # if(word[-1] == c and long len (word)): if(self.cst in self.f): return "string accepted".title() else: #count += 1 self.cst = self.90 self.trying(word, index, long=1) long += 1 # 1): long +=1 #elif(self.cst in self.f): return "string accepted".title) elif(len(self.delta[self.cst, c]) == self.cst = self.delta[(self.cst, c)][0] print('llegas?') print(long) print(self.cst) if(self.cst in self.f): return "string accepted".title) #print('count2', count) elif(self.delta[(self.cst, c)][index] == []): print('empty set') elif(word[-1] == c and long == len(word)): if(self.cst in self.f): return "string accepted".title) else: index += 1 self.cst = self.90 #print(self.cst) #break self.trying(word, index, long=1) #else: Long +=1 #continue #else: print('String not valid') # # def process_word(self, word): This method process the word entered parameters: word: A string of characters of number as string ("01010") Return: if the word is accepted o not Return: if the word is accepted o not path input('Insert your file with extension .txt: ') self.load_from_file(path) # Convert the word in strig in case that the user insert # numbers word = str(word) # change the spaces for empty string word.replace("'', '').replace('lambda', 'x').replace('epsilon', 'a') #if the word isn't in the alphabet the word isn't not accepted if(word[C] not in self.sigma): return 'Empty set' else: self.trying(word) # In this part we intend to solve for process the word # with a different approach, but we have a lot of problems count = 0 def trying (word, count=0): count += 0 #print('que u') #print('iniciando') #count = 0 for c in word: #for k,v in self.delta.items(): if(len(self.delta[self.cst, c]) > 1): self.cst = self.delta[(self.cst, c)][count] #count += 1 #if(self.delta[(self.cst, c)][count] == []): # print('empty set') if(word [-1] c): if(self.cst in self.f): return "string accepted".title) == return "string accepted".title) else: count += 1 self.cst = self.90 trying (word) elif(self.cst in self.f): return "string accepted".title) else: self.cst = self.delta[(self.cst, c)][0] if(self.cst in self.f): return "string accepted".title) elif (word[-1] == c): if(self.cst in self.f): return "string accepted".title) else: count += 1 self.cst = self.qo print(self.cst) break trying(word) else: continue #print('que u') trying (word) def str_(self): This method only show the current configuration of the automaton return: A message with te configuration of NFA # The message that the method return message = f"*"This is the current configuration of the automaton: -Automaton states: {self.q} -Alphabet: {self.sigma} -Automaton next states:{self.delta} -Initial state: {self.90} -Alphabet: {self.sigma} -Automaton next states:{self.delta} -Initial state: {self.90} -Current state: {self.cst} -Final states: {self.f} the empty transition is: {self.emp_sy}"*" return print(message) def is_valid(self, q, sigma, delta, 90, f): This method corrobote if the elements of the automaton are correct, in case que all elements are correct then the definition of NFA is valid and return True, on the contrary return the exeption NotValidConfigurationError. parameters: q: List of strings that represents the states of automata ([90, 91], [50, 51], etc). sigma: It represent the list of symbols in the alphabet ([a,b], [1,0], etc). delta: Dictionary that represent the combination in that the automata move (next states). 20: String that represent the initial state of the automata. f: List of the final state of the automata. Return: True en case that the definition of the automaton is correct the exeption NotValidConfigurationError if the definition of the automaton is not valid # create a list for the initial state and we can check # that only there is a initial element lista = [] lista.append(90) # The automaton only have one state initial rules = [len(lista) == 1, # F is a subset of a all(item in q for item in f), # qe belong the set of states (9) qo in q] # Create two counters # Count the states count = 0 # Count the extra states that are in a state with same trasition peso = 6 # Count the states count = 0 # Count the extra states that are in a state with same trasition peso = 0 check_sym [] check_empty_sy=" if all(rules): # Loop over delta for k, v in delta.items(): # Check that every transitions are from and to states of a if(len(delta[k[@], k[1]]) > 1 and delta[k[@], k[1]][count] in q): count += len(delta[k[@], k[1]]) peso += 1 # put the transition different of Lambda and epsilon if(k[1] != 'X' and k[1] != 'a'): check_sym.append(k[1]) # in case that the transition is Lambda or beta else: check_empty_sy = K[1] # in case that the state that the values of a key only have a value like state elif(delta[k[@], k[1]][C] in q): count += 1 # put the transition different of Lambda and epsilon if(k[1] != 'X' and k[1] != 'a'): check_sym.append(k[1]) # In case that the transition is Lambda or beta else: check_empty_sy = k[1] # check that all transitions are from and to states of q and that # the all symbols belong to sigma (alphabet) or that the symbol belongs to the empty string if(count == (len(delta.values() + peso) and all(item in sigma for item in check_sym) and check_empty_sy return True # In case that the automaton don't comply with anything rule else: raise Exception('NotValidConfigurationError') == self.emp_sy) Method initialize() p = NonDeterminsiticAutomaton() p.initialize() Do you want to see how the parameters should go? (y) y 9 --> ["90", "q1", "q2"] sigma --> ["0", "1"] delta --> {("90", "o"): ["93", "q1"],("91", "6"): ["42"]} 90 --> "90" f --> ["42"] empty_sy --> "X" or "2" N 9 ["90", "q1", "2"] sigma ["0", "1"] delta {("90", "o"): ["93", "q1"],("91", "o"): ["92"]} 90 = "90" f = ["q2"] emp_sy = "X" p.initialize(q, sigma, delta, q0, f, emp_sy) Do you want to see how the parameters should go? (y) n print(p.q, p.sigma, p.delta, p.q0, p.f, p.emp_sy) ['qo', 'qi', 'q2'] ['0', '1'] {('qo', '0'): ['q3', 'q1'), ('qi', '0'): ['q2']} 90 ('92'] , Method load p = NonDeterminsiticAutomaton) p.load_from_file('text_files/automaton_examples/automata.txt') p.delta 7]: {('90', '0'): ['93', 'q1'], ('qi', '0'): ['q2'], ('qi', '1'): ['q1'], ('92', '0'): ('92'], ('92', '1'): ['qi'], ('93', '0'): ['q3'], ('q8', 'A'): ['12'], ('92', 'X): ['qi']} p.9 7]: ['qo', 'qi', 'q2', 'q3'] Np.sigma B]: ['e', '1'] p.90 ]: 'qo' p.f ]: ['92'] p.emp_sy 1]: x Method process_symbol() p = NonDeterminsiticAutomaton() p.process_symbol(state='qo', symbol='0') Insert the path of your file: text_files/automaton_examples/automata.txt Set of posible next states: ['93', '41'] Method empty trasitions p = NonDeterminsiticAutomaton) p.empty_transitions('90') Insert the path of your file: text_files/automaton_examples/automata.txt Possibles states using empty trasition: ('92'] Method str() p._str_) This is the current configuration of the automaton: -Automaton states: ['qo', 'q1', 'q2', 'q'] -Alphabet: ['o', '1'] -Automaton next states:{('90', '0'): ['93', '41'], ('91', '0'): ['92'], ('91', '1'): ['91'], ('92', '0'): ['92'], ('92', 1'): ['q1'], ('93', '0'): ['93'), ('90', ''): ['92'], ('92', 'X'): ['q1']} -Initial state: 90 -Current state: 90 -Final states: ['92'] the empty transition is: X is_valido) p.load_from_file('text_files/automaton_examples/automata.txt') Na - p.4 sigma p.sigma delta p.delta 90 = p.90 f = p.f Np.is_valid(q, sigma, delta, 90, f) 1]: True