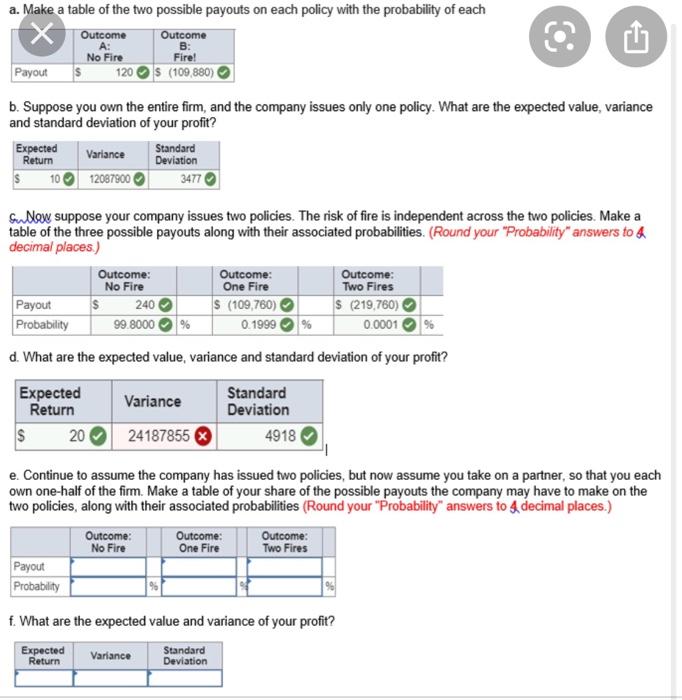
B: a. Make a table of the two possible payouts on each policy with the probability of each x Outcome Outcome No Fire Fire! Payout 120S (109,880) b. Suppose you own the entire firm, and the company issues only one policy. What are the expected value, variance and standard deviation of your profit? Expected Return Variance Standard Deviation $ 1012087900 3477 Sudlow suppose your company issues two policies. The risk of fire is independent across the two policies. Make a table of the three possible payouts along with their associated probabilities. (Round your "Probability" answers to 4 decimal places.) Outcome: Outcome: Outcome: No Fire One Fire Two Fires Payout $ 240 S (109,760) $ (219,760) Probability 99.8000 % 0.1999 0.0001 d. What are the expected value, variance and standard deviation of your profit? Expected Standard Return Variance Deviation $ 20 24187855 4918 e Continue to assume the company has issued two policies, but now assume you take on a partner, so that you each own one-half of the firm. Make a table of your share of the possible payouts the company may have to make on the two policies, along with their associated probabilities (Round your "Probability" answers to a decimal places.) Outcome: Outcome: Outcome: No Fire One Fire Two Fires Payout Probability f. What are the expected value and variance of your profit? Expected Standard Return Variance Deviation B: a. Make a table of the two possible payouts on each policy with the probability of each x Outcome Outcome No Fire Fire! Payout 120S (109,880) b. Suppose you own the entire firm, and the company issues only one policy. What are the expected value, variance and standard deviation of your profit? Expected Return Variance Standard Deviation $ 1012087900 3477 Sudlow suppose your company issues two policies. The risk of fire is independent across the two policies. Make a table of the three possible payouts along with their associated probabilities. (Round your "Probability" answers to 4 decimal places.) Outcome: Outcome: Outcome: No Fire One Fire Two Fires Payout $ 240 S (109,760) $ (219,760) Probability 99.8000 % 0.1999 0.0001 d. What are the expected value, variance and standard deviation of your profit? Expected Standard Return Variance Deviation $ 20 24187855 4918 e Continue to assume the company has issued two policies, but now assume you take on a partner, so that you each own one-half of the firm. Make a table of your share of the possible payouts the company may have to make on the two policies, along with their associated probabilities (Round your "Probability" answers to a decimal places.) Outcome: Outcome: Outcome: No Fire One Fire Two Fires Payout Probability f. What are the expected value and variance of your profit? Expected Standard Return Variance Deviation