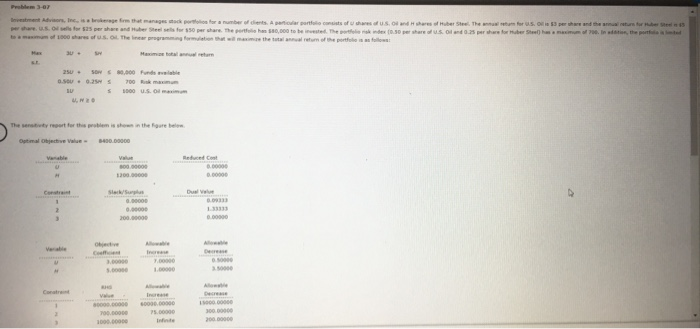
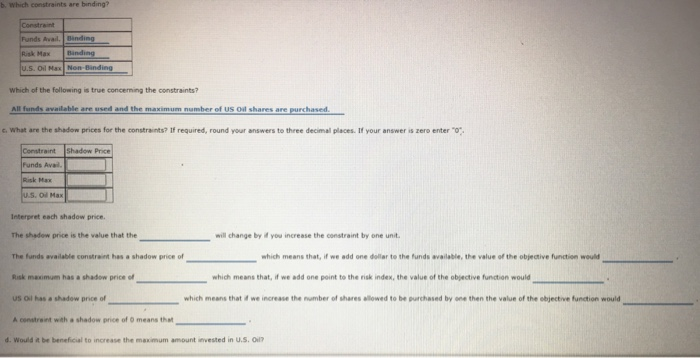
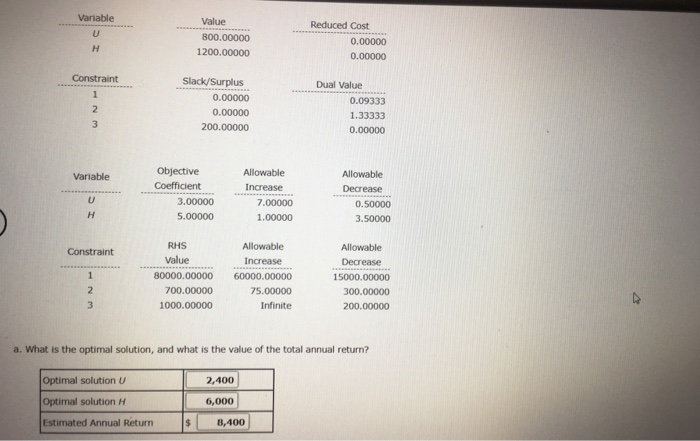
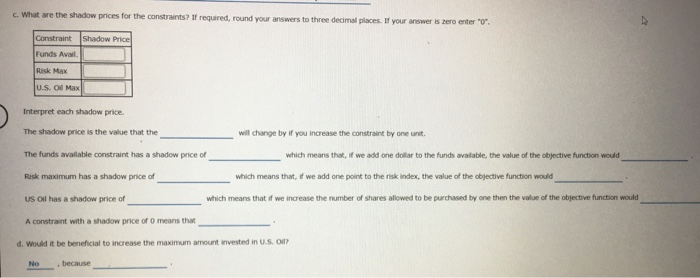
b. which constraints are binding? Funds Avail. Binding Risk Max U.S. O NaNon-Binding Which of the following is true concerning the constraints? All funds available are used and the maximum number of us oil shares are purchased c. What are the shadow prices for the constraints? If required, round your answers to three decimal places. If your answer is zero enter" Constraint shadow Price Funds Ave lu s Max Interpret each shadow price. The shadow price is the value that the will change by you increase the constraint by one unit The funds available contrast has a shadow price of which means that, if we add one dollar to the funds available, the value of the objective function would Risk maximum has a shadow price of which means that, if we add one point to the risk index, the value of the objective function would US ol has a shadow price of which means that we increase the number of shares allowed to be purchased by one then the value of the objective function would A constraint with a shadow price of means that d. Would it be beneficial to increase the maximum amount invested in U.S. Oil? Problem 3-0 Investment Advisors, Inc. is a brokerage firm that mange stock portfolios for a number of dients. A partir porto consists of shares of us. O d shares of Huber Steel The return for US. O $3 per share and the annual return for Huber Steel is $5 per share. U.S. ol sells for $25 per share and Huber Steelsells for $50 per share. The portfolio has 580,000 to be invested. The portfolio nisk index (0.50 per share of U.S. Oil and 0.25 per share for Huber Steel) has a maximum of 700. In addition, the portfolio is limited to a maximum of 1000 shares of US. Oil. The linear programming formation that will maximize the total annual return of the portfolio is as follows: Max 3U + SH Maximize total annual return 250. SOK 30,000 Funds table O SOU + 0.25HS 700 Risk mamm S 1000 US. O maximum UHO The sensitivity report for this problem is shown in the fure below. Optima Objective Value - 400.00000 Reduced cost 6000 SD 00000 1200.00000 Dual Value Slack/Surplus 0.00000 0.00000 200.00000 1. 11 0.00000 Objective A Variable Value 800.00000 1200.00000 Reduced Cost 0.00000 0.00000 Constraint Slack/Surplus 0.00000 0.00000 200.00000 Dual Value 0.09333 1.33333 0.00000 Variable Objective Coefficient 3.00000 5.00000 Allowable Increase 7.00000 1.00000 Allowable Decrease 0.50000 3.50000 Constraint RHS Value 80000.00000 700.00000 1000.00000 Allowable Increase 60000.00000 75.00000 Infinite Allowable Decrease 15000.00000 300.00000 200.00000 a. What is the optimal solution, and what is the value of the total annual return? Optimal solution U 2,400 Optimal solution H 6,000 Estimated Annual Return 8,400 b. which constraints are binding? Funds Avail. Binding Risk Max U.S. O NaNon-Binding Which of the following is true concerning the constraints? All funds available are used and the maximum number of us oil shares are purchased c. What are the shadow prices for the constraints? If required, round your answers to three decimal places. If your answer is zero enter" Constraint shadow Price Funds Ave lu s Max Interpret each shadow price. The shadow price is the value that the will change by you increase the constraint by one unit The funds available contrast has a shadow price of which means that, if we add one dollar to the funds available, the value of the objective function would Risk maximum has a shadow price of which means that, if we add one point to the risk index, the value of the objective function would US ol has a shadow price of which means that we increase the number of shares allowed to be purchased by one then the value of the objective function would A constraint with a shadow price of means that d. Would it be beneficial to increase the maximum amount invested in U.S. Oil? Problem 3-0 Investment Advisors, Inc. is a brokerage firm that mange stock portfolios for a number of dients. A partir porto consists of shares of us. O d shares of Huber Steel The return for US. O $3 per share and the annual return for Huber Steel is $5 per share. U.S. ol sells for $25 per share and Huber Steelsells for $50 per share. The portfolio has 580,000 to be invested. The portfolio nisk index (0.50 per share of U.S. Oil and 0.25 per share for Huber Steel) has a maximum of 700. In addition, the portfolio is limited to a maximum of 1000 shares of US. Oil. The linear programming formation that will maximize the total annual return of the portfolio is as follows: Max 3U + SH Maximize total annual return 250. SOK 30,000 Funds table O SOU + 0.25HS 700 Risk mamm S 1000 US. O maximum UHO The sensitivity report for this problem is shown in the fure below. Optima Objective Value - 400.00000 Reduced cost 6000 SD 00000 1200.00000 Dual Value Slack/Surplus 0.00000 0.00000 200.00000 1. 11 0.00000 Objective A Variable Value 800.00000 1200.00000 Reduced Cost 0.00000 0.00000 Constraint Slack/Surplus 0.00000 0.00000 200.00000 Dual Value 0.09333 1.33333 0.00000 Variable Objective Coefficient 3.00000 5.00000 Allowable Increase 7.00000 1.00000 Allowable Decrease 0.50000 3.50000 Constraint RHS Value 80000.00000 700.00000 1000.00000 Allowable Increase 60000.00000 75.00000 Infinite Allowable Decrease 15000.00000 300.00000 200.00000 a. What is the optimal solution, and what is the value of the total annual return? Optimal solution U 2,400 Optimal solution H 6,000 Estimated Annual Return 8,400