Background

In this assignment you will practice predicting and verifying the impact of data "nature" on the run-time of sorting algorithms. As we have seen with algorithms like insertion sort, the runtime (even worse case like Big-Oh) can be impacted by the nature of the input.

To do this, we will create three different types of input data, that may give different results when sorted. Two sorting algorithms(selection sort and insertion sort) will then be benchmarked on these three types of data. Each algorithm will be run twice, for different dataset sizes, in order to get times that we can use to apply the doubling formula. (See slide 23 (Modeling Small Datasets) in the Analysis of Algorithms slide deck for details on the doubling

formula.) The doubling formula is 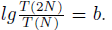.If we compute the formula, then we will be able to figure out the algorithm's Big-Oh for a particular type of input data, since they will be O(n^b).

Requirements

For this assignment you will be writing code to generate test data, as well as benchmark sorting algorithms on it (edited from Sedgewick and Wayne: 2.1.36). First, write a series of methods that generate test data that is non-uniform:

Half the data is 0s, half 1s.

Half the data is 0s, half the remainder is 1s, half the reminder is 2s, and so forth.

Half the data is 0s, half random int values (can use nextInt() from Java's Random package) .

Each of these three techniques should be implemented as a static method that takes an integer representing the size of a dataset and returns an integer array containing that number of elements generated with the corresponding rule. Randomize (shuffle) the contents of the array after you populate it.

Using the three methods you implement, develop and test hypotheses about the effect of input on the performance of two of the algorithms (your choice) we have covered. (Get their source code from BlackBoard.)

The program should contain your hypotheses (3 per algorithm) as comments: describe what you think the running time will look like (O(n)? O(n²)? O(n³)?) on each data set and explain briefly why you think that. As long as your ideas make sense, you will receive full credit on the hypotheses

For each of the two sorting algorithms, you should run them on the three types of test data. Test them with datasets size of 2048 and 4096. Time each of these twelve tests with the Stopwatch class given in class. (If your system is so fast you don't get good results, you may increase the dataset size.)

Display the result of applying the doubling formula to the run times from the 2048 and 4096 test pairs to get the power (b) for that algorithm on that type of input.

Testing

The main functionality to test is the methods that generate test data. You will want to run them multiple times, on different sizes, and display their output. Check that the output matches the patterns required above. There isn't much else to test for this homework. The algorithms you are benchmarking have already been tested for correctness. Optionally, you may want to try giving an input that is pure random numbers to each of the algorithms and checking if your doubling formula code gives the algorithms expected Big-Oh.

The Stopwatch Class is given:

public class Stopwatch {

private final long start;

public Stopwatch() {

start = System.currentTimeMillis();

}

public double elapsedTime() {

long now = System.currentTimeMillis();

return (now - start) / 1000.0;

}

}

lg > T(N) lg > T(N)