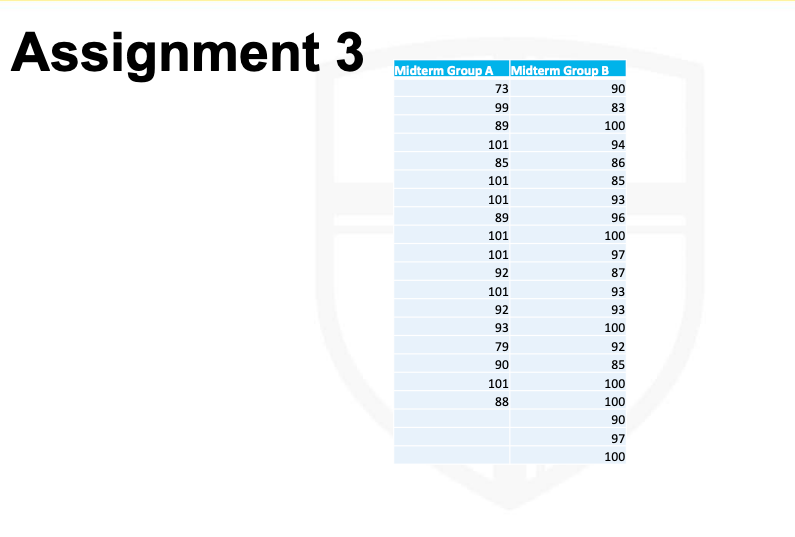
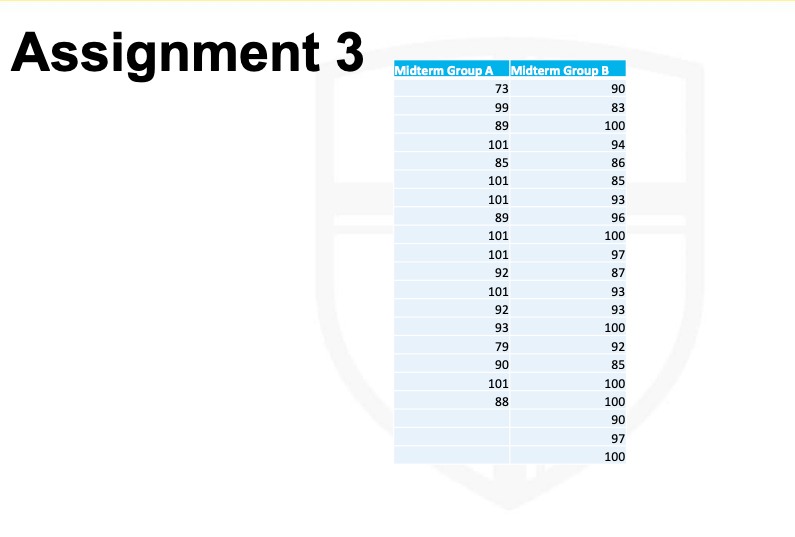
Background Information to help solve the problem: In many instances, it is necessary to compare numeric data from two groups to see which one is greater than the other. How do we know that random chance did not cause the apparent difference between groups if one group had a mean score of 79 and the other produced an average score of 81? In this instance, I am thinking about continuous data, means, and normal curves, whether skewed or not. Such a situation calls for a t-test. Before we go further, it is important to point out the situational differences between a paired samples (aka, matched pairs, repeated measures, or correlated samples) and independent samples t-test. An independent samples t-test is used to compare data from two groups when there is no direct connection between the two groups (i.e., males and females). A paired samples t-test is used in a pre- and post-test scenario or if members of two groups share a common trait such as being twins. Another example would be data on freshmen infractions as compared to the same students' infractions tallied during their sophomore year. If you were comparing different groups of freshmen to sophomores, then it would require an independent samples t-test.

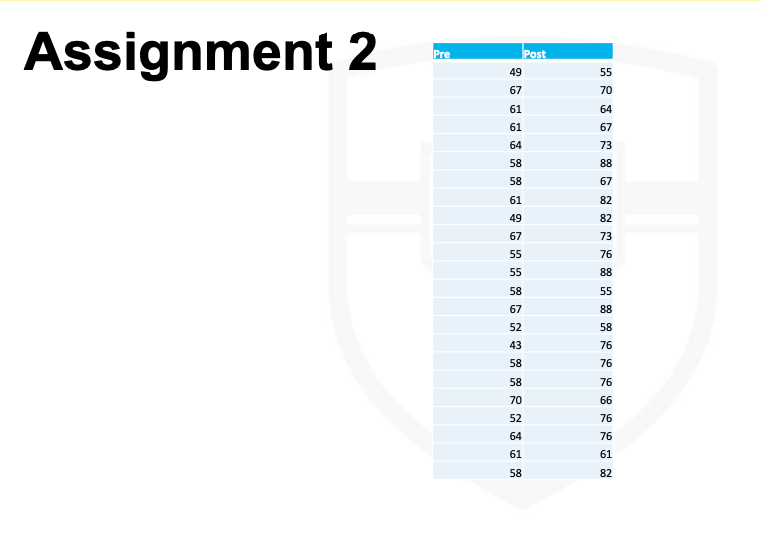
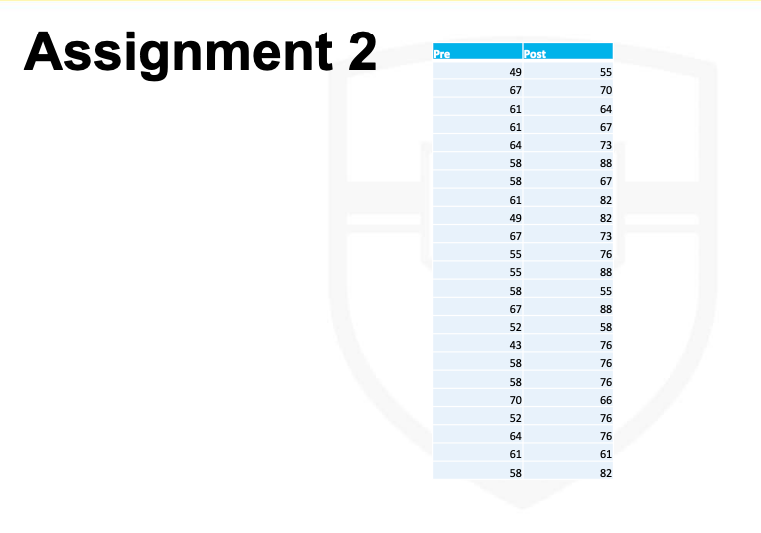
In assignment 2, you will find actual student data in an academic program. In exercise 2, data are pre and post-test Composite Test Scores. Here is the question, "Did students who finished the program have a significantly different score at the end of their respective programs? Why?