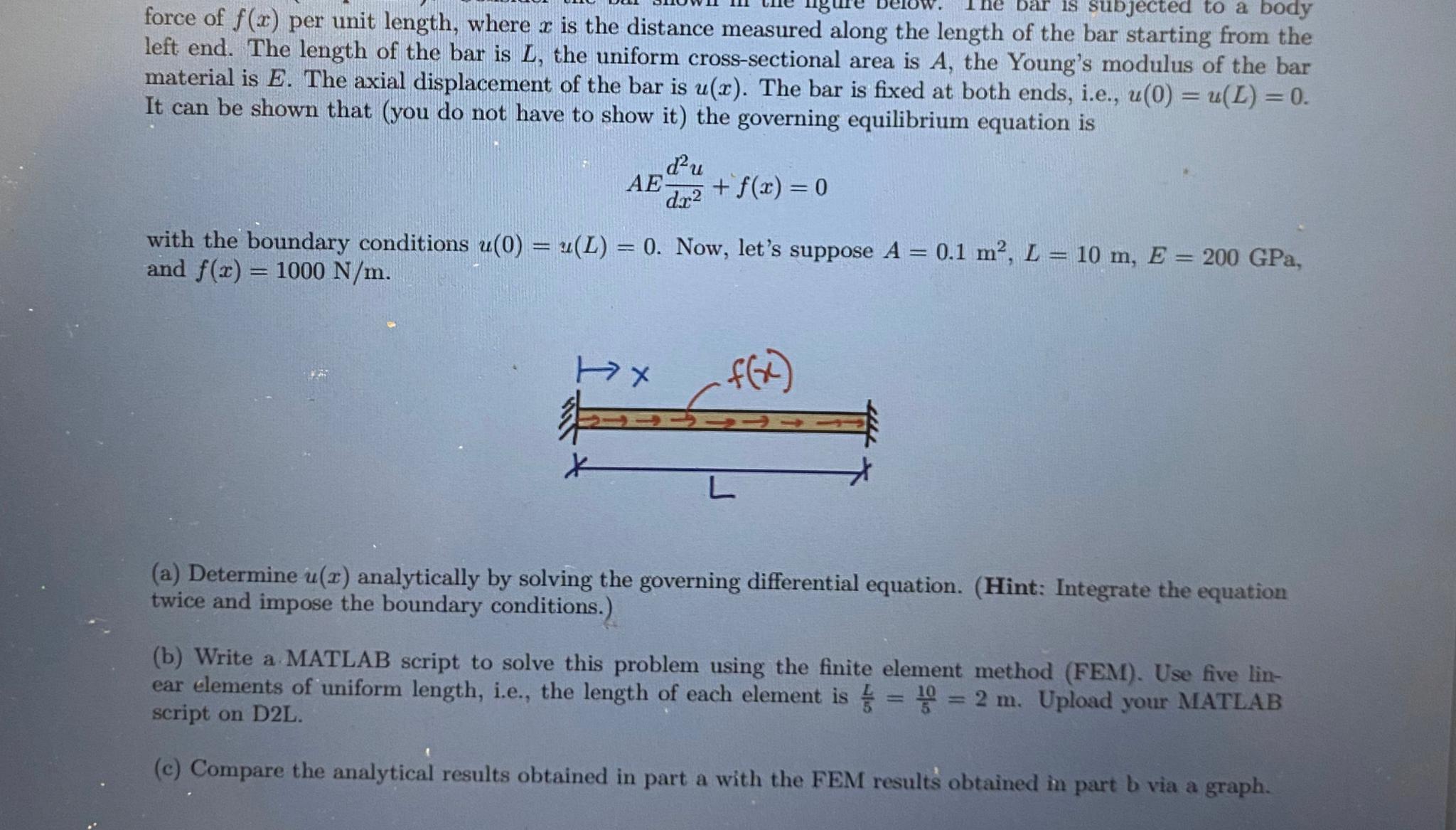
bar is subjected to a body force of f(x) per unit length, where x is the distance measured along the length of the bar starting from the left end. The length of the bar is L, the uniform cross-sectional area is A, the Young's modulus of the bar material is E. The axial displacement of the bar is u(x). The bar is fixed at both ends, i.e., u(0) = u(L) = 0. It can be shown that (you do not have to show it) the governing equilibrium equation is AE du dx2 +f(x) = 0 - with the boundary conditions u(0) = (L) = 0. Now, let's suppose A = 0.1 m, L = 10 m, E = 200 GPa, and f(x) = 1000 N/m. Hx f(x) L (a) Determine u(x) analytically by solving the governing differential equation. (Hint: Integrate the equation twice and impose the boundary conditions.) (b) Write a MATLAB script to solve this problem using the finite element method (FEM). Use five lin- ear elements of uniform length, i.e., the length of each element is = 10 = 2 m. Upload your MATLAB script on D2L. (c) Compare the analytical results obtained in part a with the FEM results obtained in part b via a graph.