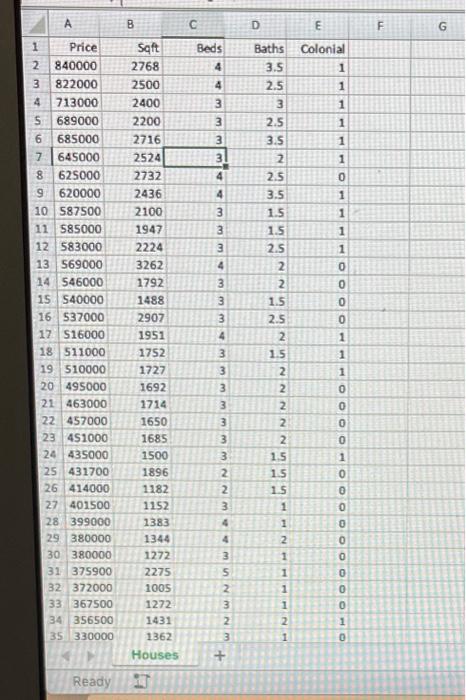
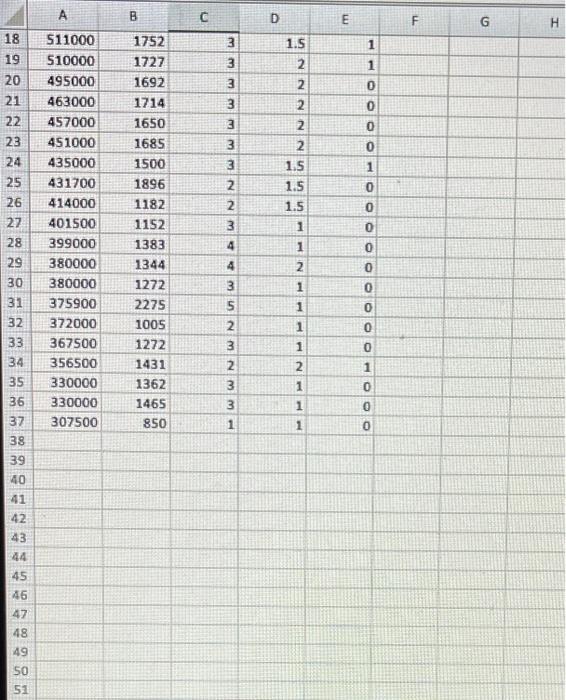
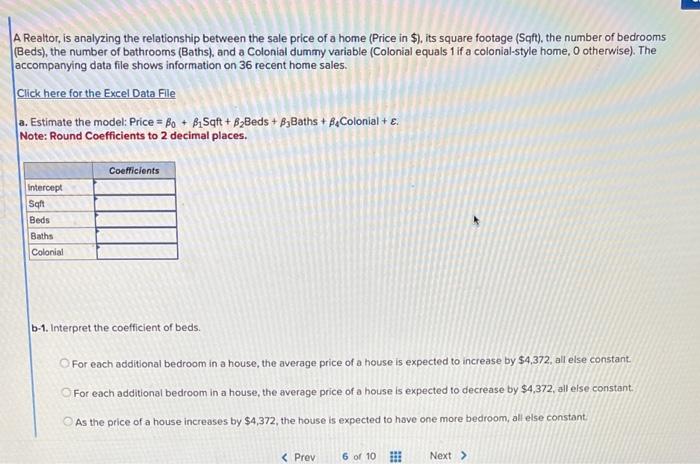
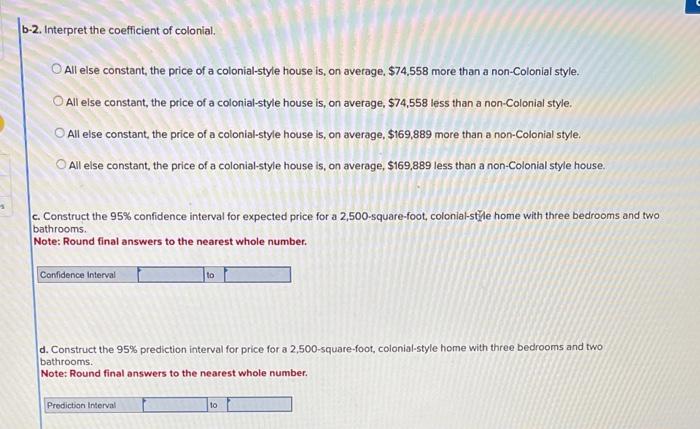
\begin{tabular}{|l|l|r|r|r|r|r|} \hline & \multicolumn{1}{|l|}{ A } & & & & \end{tabular} A Realtor, is analyzing the relationship between the sale price of a home (Price in \$). its square footage (Sqft), the number of bedrooms (Beds), the number of bathrooms (Baths), and a Colonial dummy variable (Colonial equals 1 if a colonial-style home, 0 otherwise). The accompanying data file shows information on 36 recent home sales. Click here for the Excel Data File a. Estimate the model: Price =0+1Sqft+2Beds+3 Baths +4 Colonial +. Note: Round Coefficients to 2 decimal places. b-1. Interpret the coefficient of beds. For each additional bedroom in a house, the average price of a house is expected to increase by $4,372, all else constant: For each additional bedroom in a house, the average price of a house is expected to decrease by $4,372, all else constant. As the price of a house increases by $4,372, the house is expected to hove one more bedroom, all else constant. b-2. Interpret the coefficient of colonial. All else constant, the price of a colonial-style house is, on average, $74,558 more than a non-Colonial style. All else constant, the price of a colonial-style house is, on average, $74,558 less than a non-Colonial style. All else constant, the price of a colonial-style house is, on average, $169,889 more than a non-Colonial style. All else constant, the price of a colonial-style house is, on average, $169,889 less than a non-Colonial style house. c. Construct the 95% confidence interval for expected price for a 2,500-square-foot, colonial-sthle home with three bedrooms and two bathrooms. Note: Round final answers to the nearest whole number. d. Construct the 95% prediction interval for price for a 2,500-square-foot, colonial-style home with three bedrooms and two bathrooms. Note: Round final answers to the nearest whole number. \begin{tabular}{|l|l|r|r|r|r|r|} \hline & \multicolumn{1}{|l|}{ A } & & & & \end{tabular} A Realtor, is analyzing the relationship between the sale price of a home (Price in \$). its square footage (Sqft), the number of bedrooms (Beds), the number of bathrooms (Baths), and a Colonial dummy variable (Colonial equals 1 if a colonial-style home, 0 otherwise). The accompanying data file shows information on 36 recent home sales. Click here for the Excel Data File a. Estimate the model: Price =0+1Sqft+2Beds+3 Baths +4 Colonial +. Note: Round Coefficients to 2 decimal places. b-1. Interpret the coefficient of beds. For each additional bedroom in a house, the average price of a house is expected to increase by $4,372, all else constant: For each additional bedroom in a house, the average price of a house is expected to decrease by $4,372, all else constant. As the price of a house increases by $4,372, the house is expected to hove one more bedroom, all else constant. b-2. Interpret the coefficient of colonial. All else constant, the price of a colonial-style house is, on average, $74,558 more than a non-Colonial style. All else constant, the price of a colonial-style house is, on average, $74,558 less than a non-Colonial style. All else constant, the price of a colonial-style house is, on average, $169,889 more than a non-Colonial style. All else constant, the price of a colonial-style house is, on average, $169,889 less than a non-Colonial style house. c. Construct the 95% confidence interval for expected price for a 2,500-square-foot, colonial-sthle home with three bedrooms and two bathrooms. Note: Round final answers to the nearest whole number. d. Construct the 95% prediction interval for price for a 2,500-square-foot, colonial-style home with three bedrooms and two bathrooms. Note: Round final answers to the nearest whole number