Below is some useful material.

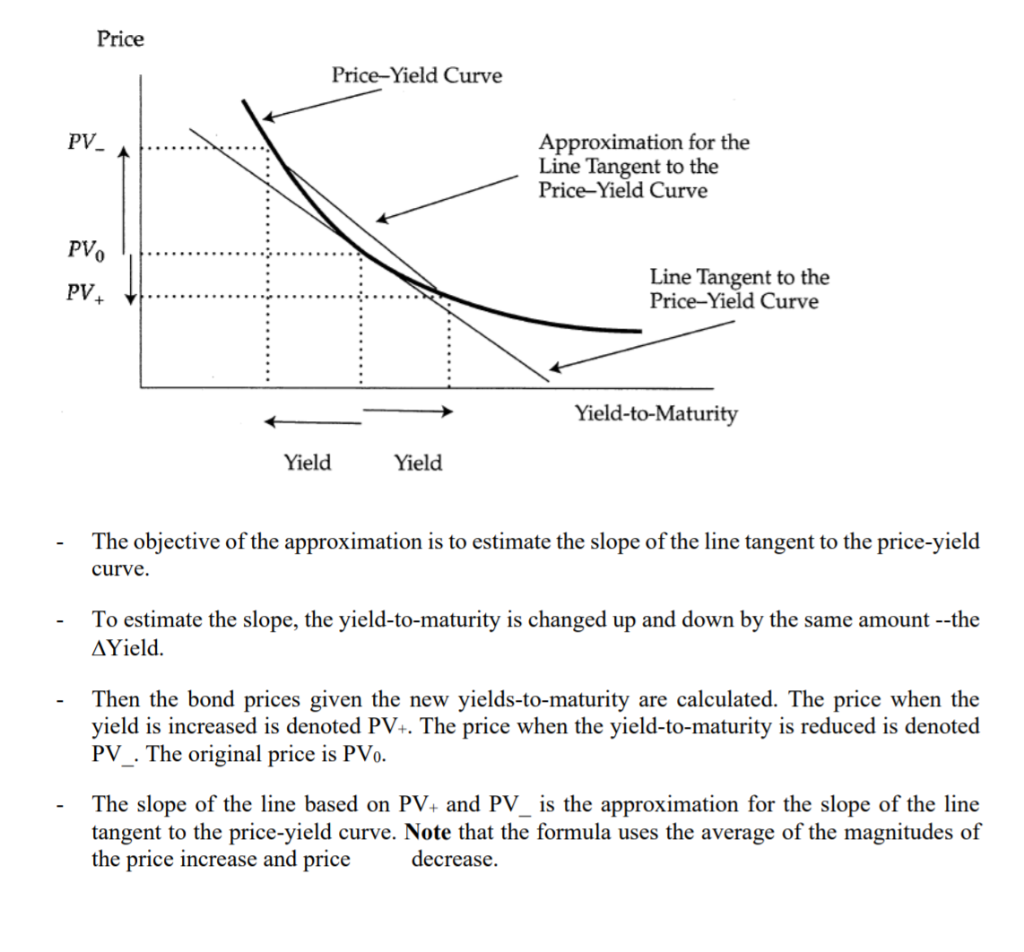
A portfolio manager wants to estimate the interest rate risk of a bond using duration. The current price of the bond is 82. A valuation model found that if interest rates decline 30 basis points, the price will increase to 83.50 and if interest rates increase by 30 basis points, the price will decline to 80.75. What is the duration of this bond? [Read Attachment #1 before attempting.) Macaulay, Modified and Approximate Modified Durations Macaulay duration (MacDur) is named after Frederick Macaulay, the Canadian economist who first wrote about the statistic in a book published in 1938. Macaulay duration is an estimate of a bond's interest rate risk (price sensitivity to interest rate change) based on time, in periods, to receipt of the bond's promised payments. It can be converted to annual duration by dividing by the number of periods in the year. It is a weighted average of the time to receipt of the bond's promised payments, where the weights are the shares of the full price that correspond to each of the bond's promised future payments. -------------------------------- - Modified duration (ModDur) is the Macaulay duration statistic divided by one plus the yield per period (ModDur=MacDur/ (1 + YTM)). Although modified duration might seem to be just a Macaulay duration with minor adjustments, it has an important application in risk measurement: Modified duration provides an estimate of the percentage price change for a bond given a change in its yield-to-maturity. The modified duration statistic for a fixed-rate bond is easily obtained if the Macaulay duration is already known. An alternative approach is to approximate modified duration directly. (PV-)-(PV) ApproxModDur = - 2 (AYield) * (PV) where - PV+ is the price when the yield is increased - PV is the price when the yield-to-maturity is reduced PVo is the original price Price Price-Yield Curve Approximation for the Line Tangent to the Price-Yield Curve Line Tangent to the Price-Yield Curve Yield-to-Maturity Yield Yield The objective of the approximation is to estimate the slope of the line tangent to the price-yield curve. To estimate the slope, the yield-to-maturity is changed up and down by the same amount --the AYield. Then the bond prices given the new yields-to-maturity are calculated. The price when the yield is increased is denoted PV+. The price when the yield-to-maturity is reduced is denoted PV_. The original price is PVO. The slope of the line based on PV+ and PV is the approximation for the slope of the line tangent to the price-yield curve. Note that the formula uses the average of the magnitudes of the price increase and price decrease