Question
Below is the prompt for my code and the code below that. I am getting errors when I try to run on Linux. If you
Below is the prompt for my code and the code below that. I am getting errors when I try to run on Linux. If you could help me solve my errors using my code, thatd be great. Thank you 
test_complex.cpp
#include
int main() { //complex_number c1(2.3, 4.8),c2(8,1); //cout
assert (c1.get_real_part() == 2.3);
assert (c1.get_imag_part() == 4.8);
complex_number c2 (2.6);
assert (c2.get_real_part() == 2.6);
assert (c2.get_imag_part() == 0.0);
complex_number c3;
assert (c3.get_real_part() == 0.0);
assert (c3.get_imag_part() == 0.0);
assert (conjugate(c1).get_real_part() == 2.3);
assert (conjugate(c1).get_imag_part() == -4.8);
assert (abs (complex_modulus (c1) - 5.322593353)
complex_number c4 (2.3, 4.8);
assert (c1 == c4);
assert (c1 != c2);
complex_number c5 (1.3, -4.1);
complex_number c6 = c4 + c5;
assert (abs (c6.get_real_part() - 3.6)
assert (abs (c6.get_imag_part() - 0.7)
complex_number c7 = c4 - c5;
assert (abs (c7.get_real_part() - 1.0)
assert (abs (c7.get_imag_part() - 8.9)
complex_number c8 = c4 * c5;
assert (abs (c8.get_real_part() - 22.67)
assert (abs (c8.get_imag_part() + 3.19)
complex_number c9 = c4 / c5;
cout
return EXIT_SUCCESS; }
Complex_number.cpp
#include
#include "complex_number.h"
complex_number::complex_number(double r, double i) { real_part = r;
imag_part = i; } double complex_number::get_real_part () const { return real_part; } double complex_number::get_imag_part () const { return imag_part; } complex_number operator + (const complex_number& c1, const complex_number& c2) { complex_number ob; ob.real_part=c1.real_part+c2.real_part; ob.imag_part=c1.imag_part+c2.imag_part;
return(ob); } std::ostream& operator
{ output
return(output);
}
complex_number operator - (const complex_number& c1, const complex_number& c2)
{ complex_number ob;
ob.real_part=c1.real_part-c2.real_part;
ob.imag_part=c1.imag_part-c2.imag_part;
return(ob);
} complex_number operator * (const complex_number& c1, const complex_number& c2)
{
complex_number ob;
ob.real_part=(c1.real_part*c2.real_part)+(0-(c1.imag_part*c2.imag_part));
ob.imag_part=(c1.real_part*c2.imag_part)+(c1.imag_part*c2.real_part);
return(ob);
} complex_number operator / (const complex_number& c1, const complex_number& c2)
{
complex_number ob;
double den=c2.real_part*c2.real_part+c2.imag_part+c2.imag_part;
ob.real_part=(c1.real_part*c2.real_part+c1.imag_part*c2.imag_part)/den;
ob.imag_part=((c1.imag_part*c2.real_part)-(c1.real_part*c2.imag_part))/den;
return(ob);
} complex_number conjugate (const complex_number& c)
{ complex_number ob;
ob.real_part=c.real_part;
ob.imag_part=0-c.imag_part;
return(ob);
} double complex_modulus (const complex_number& c)
{ return(sqrt(c.real_part*c.real_part+c.imag_part*c.imag_part));
}
bool operator == (const complex_number& c1, const complex_number& c2)
{
if(c1.real_part==c2.real_part&&c1.imag_part==c2.imag_part) return(true);
return(false);
}
bool operator != (const complex_number& c1, const complex_number& c2)
{
if(c1.real_part==c2.real_part&&c1.imag_part==c2.imag_part) return(false);
return(true);
}
complex_number.h
#include
using namespace std;
#ifndef COMPLEX_NUMBER_H
#define COMPLEX_NUMBER_H
class complex_number
{
private:
double real_part;
double imag_part;
public:
complex_number(double r = 0.0, double i = 0.0);
// postcondition: complex with given components has been created
double get_real_part () const;
// returned: real part of complex number
double get_imag_part () const;
// returned: imaginary part of complex number
friend complex_number operator + (const complex_number& c1, const complex_number& c2);
friend std::ostream& operator
// returned: sum of c1 and c2
friend complex_number operator - (const complex_number& c1, const complex_number& c2);
// returned: difference of c1 and c2
friend complex_number operator * (const complex_number& c1, const complex_number& c2);
// returned: product of c1 and c2
friend complex_number operator / (const complex_number& c1, const complex_number& c2);
// precondition: c2 is not the zero of complex numbers
// returned: quotient of c1 and c2
friend complex_number conjugate (const complex_number& c);
// returned: conjugate of c
friend double complex_modulus (const complex_number& c);
// returned: modulus of c
friend bool operator == (const complex_number& c1, const complex_number& c2);
// returned whether c1 and c2 are equal to each other
friend bool operator != (const complex_number& c1, const complex_number& c2);
// returned whether c1 and c2 are not equal to each other
// postcondition: c has been put on the output stream output
// returned: modified output stream output
};
#endif // COMPLEX_NUMBER_H
Errors.

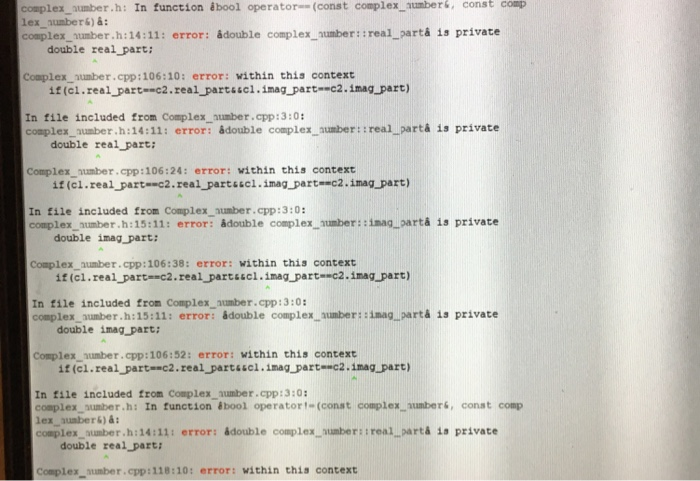
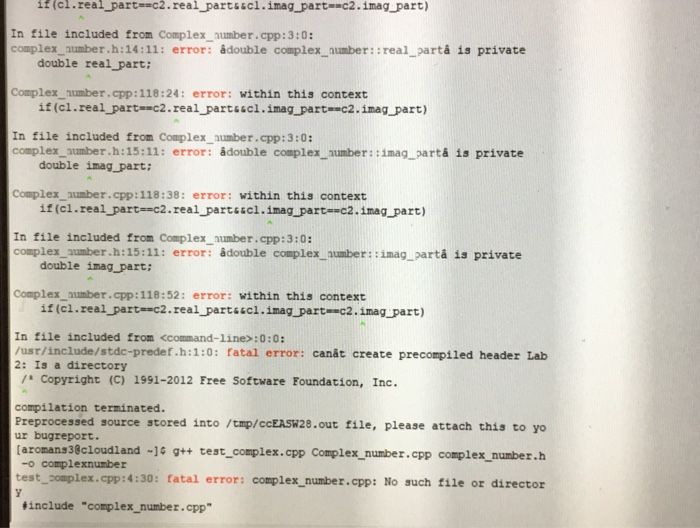
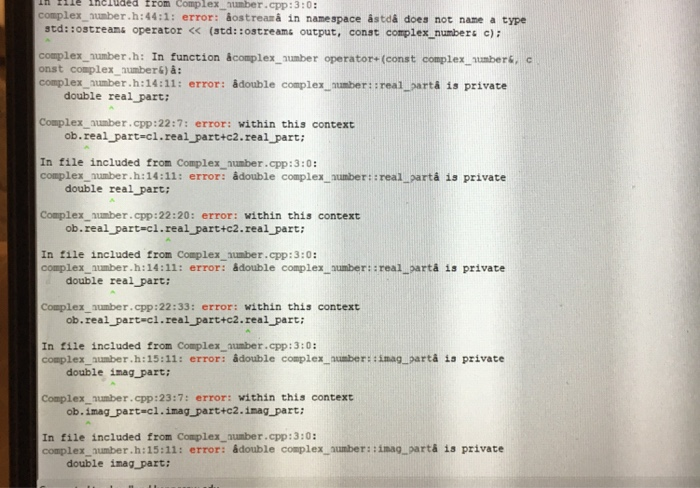
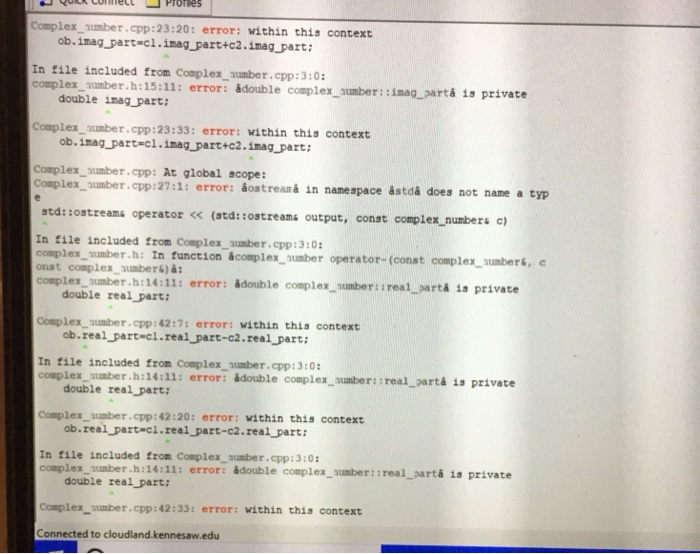
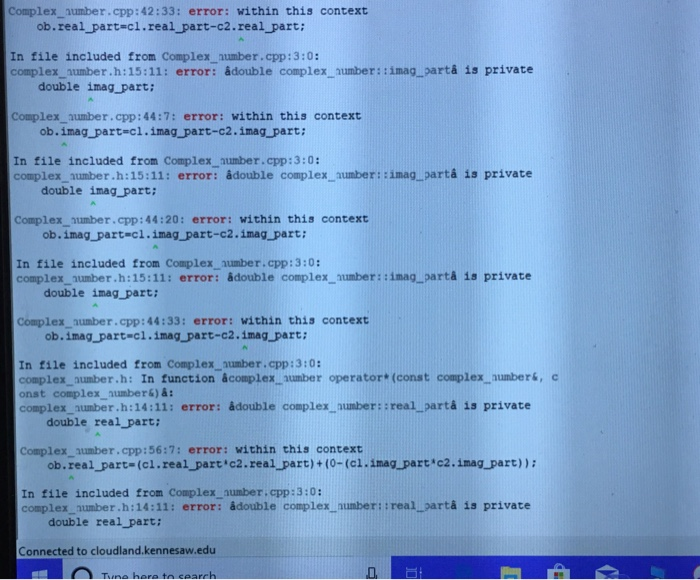


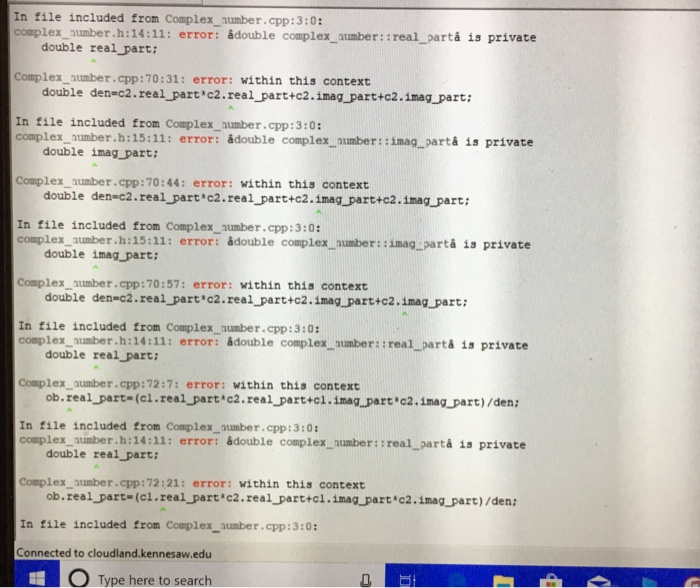
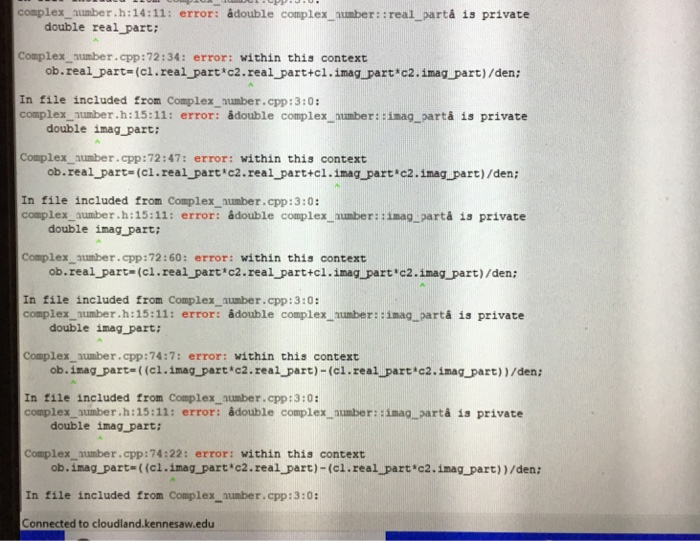

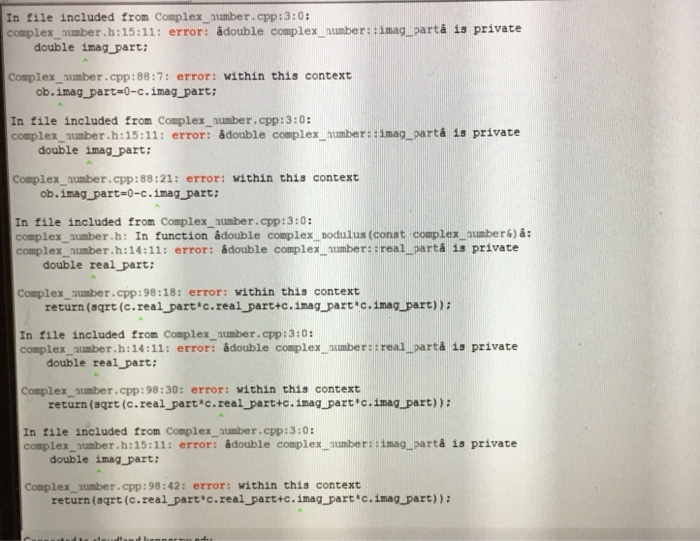
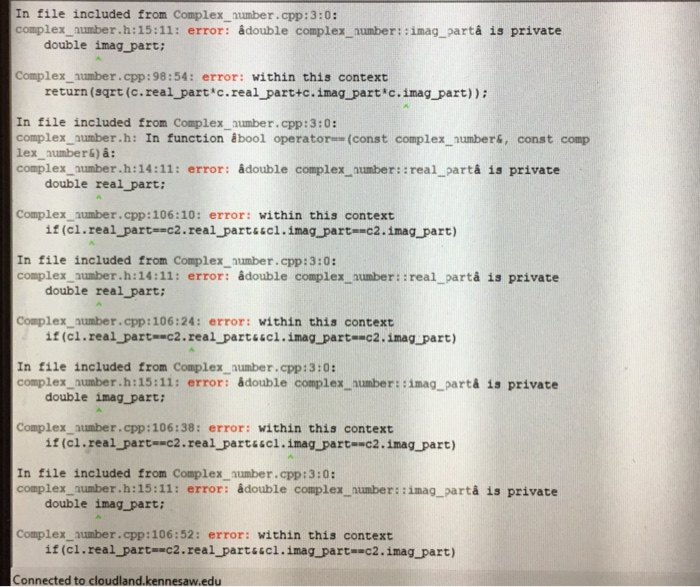
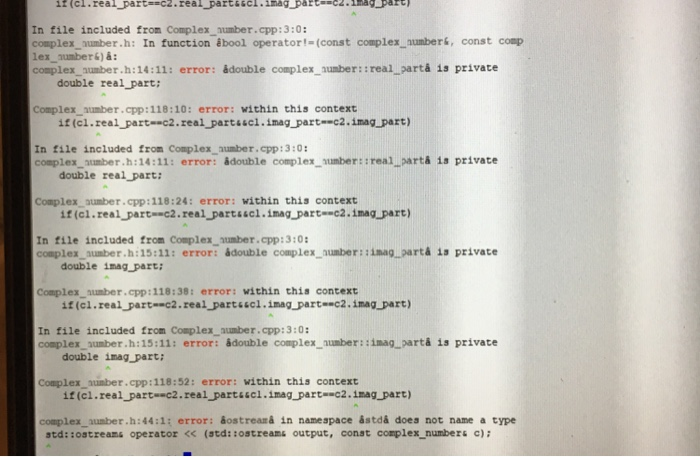
Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


