Beta distributor

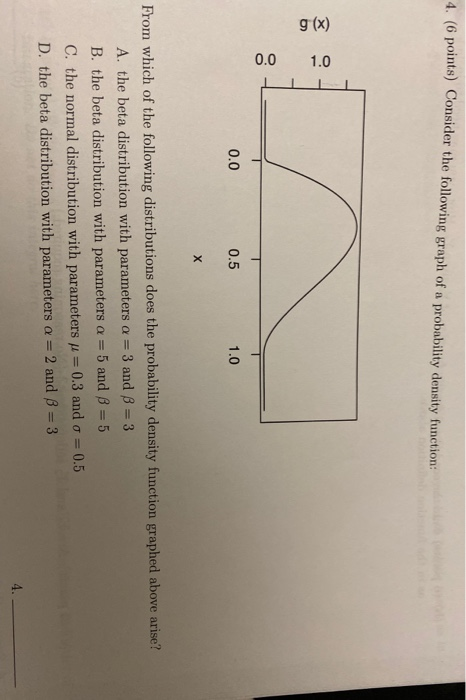
1. Let {N1(t],t 33 0} he a Poisson Process with rate A. Can Z[t) = aN1(t) + 6N2(t] ever be a Poisson Process, where 0: and 3 are some non-zero constants. In other words, are there any values of o, ,8, and N2(t) such that {Z (t): 2 0} is a Poisson Process. Please note that {N2[t),t 2 U} is not allowed to be either a Poisson Process, and is also not allowed to be a trivial random process (eg.1 it is not a constant over all time). Carefully prove or disprove. Question# 1: Customers arrive at the neighborhood bookstore according to a Poisson process with an average rate of 7 customers per hour. If the amount of money that each customer paid is uniformly distributed between $80 and $200. What is the mean and variance of the total amount of money that the customers pay out in a one-hour period spend in the bookstore? Question# 2: Complete the following sentences: 1) If the random process X(t) represents the total number of events occurred in the interval [0, t) then, the X(t) is called a - 2) The Interarrival times for the Poisson process are identical independent --------- distributed. 3) Poisson Process has an ----- ---- and increments. 4) X(t) - X(s) in a Poisson Process represent that the number of events occurred in the interval is 5 events. 5) Poisson process {X(t)|t 2 0} is a counting process which X(t) are ------- and ------ Values.The beta distribution with shape parameters a > 0 and f > 0 has pdf fx (x) = - B(a,B) for x E [0,1] where r(a)r(B) B(a. P) =T(a + 8) a) Show that the beta distribution exhibits mirror symmetry: if X -Beta(a, 8) then 1 - X-Beta (8, a) b) If X-Beta(a, 1) show that - In X ~Exp(a) c) If X~Beta(1,1) show that X-U(0,1) d) Show that the beta distribution Beta(a, () has mode XE 2-a-B4. (6 points) Consider the following graph of a probability density function: 1.0 (x) 6 0'0 0.0 0.5 From which of the following distributions does the probability density function graphed above arise? A. the beta distribution with parameters o = 3 and 3 = 3 B. the beta distribution with parameters o = 5 and 3 = 5 C. the normal distribution with parameters / = 0.3 and o = 0.5 D. the beta distribution with parameters o = 2 and 3 = 3