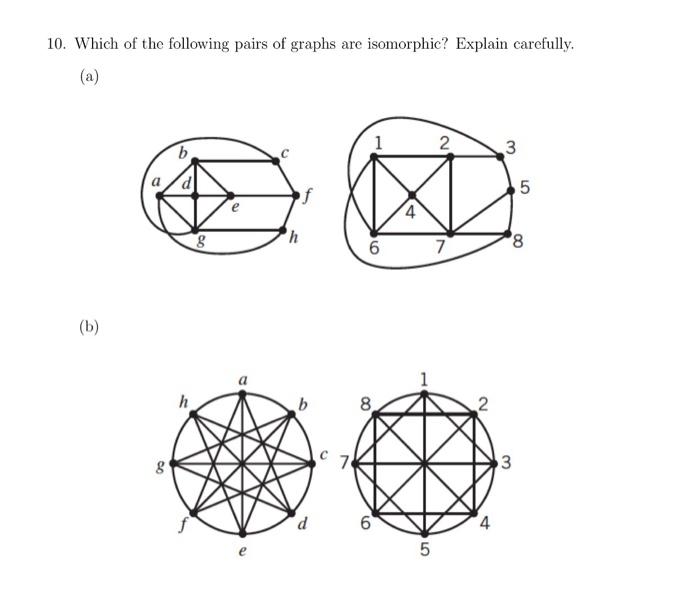
2. If the simple graph G has n vertices and m edges, how many edges does G have? 3. Suppose that graph G is isomorphic to graph G. Show that if G contains a cycle of length k so does G'. 4. Prove that, if two different cycles of a graph G each contain an edge e, then G has a cycle that doesn't contain e. 5. Show that two graphs G and H are isomorphic if and only if their complements G and H are isomorphic. 6. Let G be a k-regular bipartite graph (k21), show that the two partitions have the same size. 7. A bridge of a connected graph G is an edge e such that G-e is disconnected. Prove that if e is a bridge, then e doesn't lie of any cycle in G. 8. Let G be a graph where all vertices have degree at least 8, for some 82 2. Prove that G contains a cycle of length at least 8 + 1. 9. A simple graph that is isomorphic to its complement is called self-complementary. Prove that, if the graph G is self-complementary, then G has 4k or 4k+1 vertices, where k is an integer. 10. Which of the following pairs of graphs are isomorphic? Explain carefully. (a) (b) g g a h d 6 8 4 5 2 7 4 3 LO 3 5 8