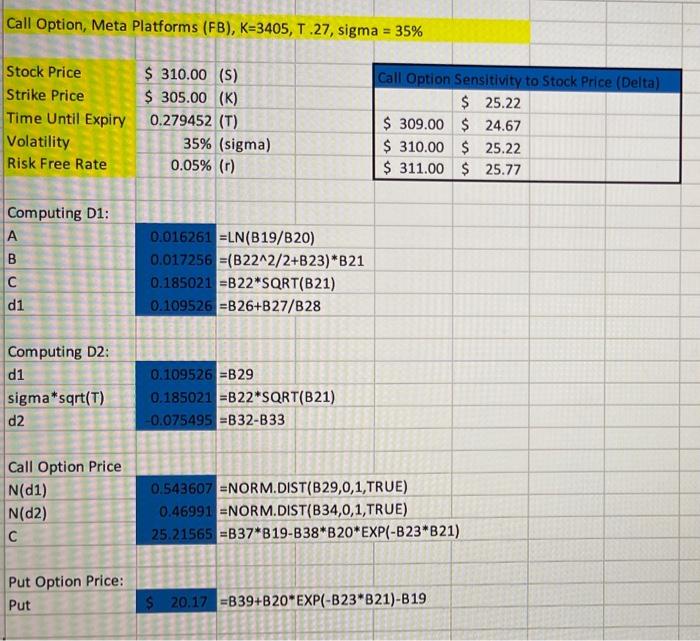
Build a Black-Scholes option pricing calculator and use it to price a call option on Meta Platforms
(FB) stock with a strike of $305, expiring on March 18, 2022. Use implied volatility of 35%, a
current stock price of $310, a current date of 12/06/2021 and a risk-free rate of .05% to show the Black-Scholes option price is approximately $25.70. Use data tables to compute the delta, vega, and theta of this call option and answer the following questions:
1) If the FB stock price increases by $1, how will the value of the call option change? How do call
option prices respond to changes in time to expiry, volatility, and strike price? Explain your
answers.
2 What is the corresponding put option price? How do put option prices respond to changes in
the current stock price, time to expiry, volatility, and strike price? Explain your responses.

Build a Black-Scholes option pricing calculator and use it to price a call option on Meta Platforms (FB) stock with a strike of $305, expiring on March 18, 2022. Use implied volatility of 35%, a current stock price of $310, a current date of 12/06/2021 and a risk-free rate of .05% to show the Black-Scholes option price is approximately $25.70. Use data tables to compute the delta, vega, and theta of this call option and answer the following questions: 1) If the FB stock price increases by $1, how will the value of the call option change? How do call option prices respond to changes in time to expiry, volatility, and strike price? Explain your answers. 2) What is the corresponding put option price? How do put option prices respond to changes in the current stock price, time to expiry, volatility, and strike price? Explain your responses. Call Option, Meta Platforms (FB), K=3405, T.27, sigma = 35% Stock Price Strike Price Time Until Expiry Volatility Risk Free Rate $ 310.00 (5) $ 305.00 (K) 0.279452 (T) 35% (sigma) 0.05% (0) Call Option Sensitivity to Stock Price (Delta) $ 25.22 $ 309.00 $ 24.67 $ 310.00 $ 25.22 $ 311.00 $ 25.77 Computing D1: B d1 0.016261 ELN(B19/B20) 0.017256 =(B2212/2+B23)*B21 0.185021 =B22*SQRT(B21) 0.109526 =B26+B27/B28 Computing D2: d1 sigma*sqrt(T) d2 0.109526 =B29 0.185021 =B22*SQRT(321) -0.075495 =B32-B33 Call Option Price N(dl) N(d2) 0.543607 ENORM.DIST(B29,0,1,TRUE) 0.46991 ENORM.DIST(B34,0,1,TRUE) 25.21565 =B37*819-838*B20*EXP(-B 23*B21) Put Option Price: Put $ 20.17 =B39+B20*EXP(-B23*B21)-B19 w a Call Option Sensitivity To Strike Price Call Option Sensitivity to Time (Theta) 25.21565 0.276712 25.1044 0.279452 25.21565 0.282192 25.32636 Build a Black-Scholes option pricing calculator and use it to price a call option on Meta Platforms (FB) stock with a strike of $305, expiring on March 18, 2022. Use implied volatility of 35%, a current stock price of $310, a current date of 12/06/2021 and a risk-free rate of .05% to show the Black-Scholes option price is approximately $25.70. Use data tables to compute the delta, vega, and theta of this call option and answer the following questions: 1) If the FB stock price increases by $1, how will the value of the call option change? How do call option prices respond to changes in time to expiry, volatility, and strike price? Explain your answers. 2) What is the corresponding put option price? How do put option prices respond to changes in the current stock price, time to expiry, volatility, and strike price? Explain your responses. Call Option, Meta Platforms (FB), K=3405, T.27, sigma = 35% Stock Price Strike Price Time Until Expiry Volatility Risk Free Rate $ 310.00 (5) $ 305.00 (K) 0.279452 (T) 35% (sigma) 0.05% (0) Call Option Sensitivity to Stock Price (Delta) $ 25.22 $ 309.00 $ 24.67 $ 310.00 $ 25.22 $ 311.00 $ 25.77 Computing D1: B d1 0.016261 ELN(B19/B20) 0.017256 =(B2212/2+B23)*B21 0.185021 =B22*SQRT(B21) 0.109526 =B26+B27/B28 Computing D2: d1 sigma*sqrt(T) d2 0.109526 =B29 0.185021 =B22*SQRT(321) -0.075495 =B32-B33 Call Option Price N(dl) N(d2) 0.543607 ENORM.DIST(B29,0,1,TRUE) 0.46991 ENORM.DIST(B34,0,1,TRUE) 25.21565 =B37*819-838*B20*EXP(-B 23*B21) Put Option Price: Put $ 20.17 =B39+B20*EXP(-B23*B21)-B19 w a Call Option Sensitivity To Strike Price Call Option Sensitivity to Time (Theta) 25.21565 0.276712 25.1044 0.279452 25.21565 0.282192 25.32636