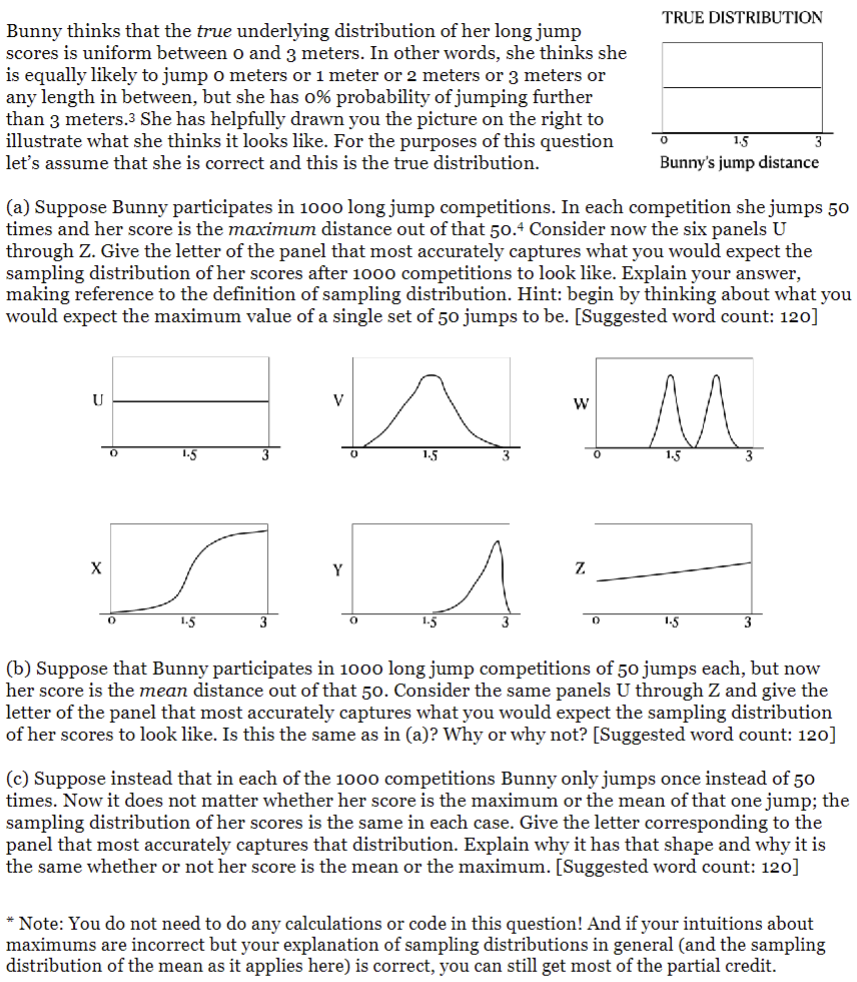
Bunny thinks that the true underlying distribution of her long jump scores is uniform between 0 and 3 meters. In other words, she thinks she is equally likely to jump o meters or 1 meter or 2 meters or 3 meters or any length in between, but she has 0% probability of jumping further than 3 meters.3 She has helpfully drawn you the picture on the right to illustrate what she thinks it looks like. For the purposes of this question let's assume that she is correct and this is the true distribution. 0 TRUE DISTRIBUTION 1.5 Bunny's jump distance (a) Suppose Bunny participates in 1000 long jump competitions. In each competition she jumps 50 times and her score is the maximum distance out of that 50.4 Consider now the six panels U through Z. Give the letter of the panel that most accurately captures what you would expect the sampling distribution of her scores after 1000 competitions to look like. Explain your answer, making reference to the definition of sampling distribution. Hint: begin by thinking about what you would expect the maximum value of a single set of 50 jumps to be. [Suggested word count: 120] U W H A M 1.5 X 1.5 Y 1.5 Z 1.5 3 (b) Suppose that Bunny participates in 1000 long jump competitions of 50 jumps each, but now her score is the mean distance out of that 50. Consider the same panels U through Z and give the letter of the panel that most accurately captures what you would expect the sampling distribution of her scores to look like. Is this the same as in (a)? Why or why not? [Suggested word count: 120] (c) Suppose instead that in each of the 1000 competitions Bunny only jumps once instead of 50 times. Now it does not matter whether her score is the maximum or the mean of that one jump; the sampling distribution of her scores is the same in each case. Give the letter corresponding to the panel that most accurately captures that distribution. Explain why it has that shape and why it is the same whether or not her score is the mean or the maximum. [Suggested word count: 120] *Note: You do not need to do any calculations or code in this question! And if your intuitions about maximums are incorrect but your explanation of sampling distributions in general (and the sampling distribution of the mean as it applies here) is correct, you can still get most of the partial credit. Q10 [14% of total mark] The long jump is an unusual event because a person is evaluated based on their best attempt out of several. In sprinting, like most events, there is only one attempt and the winner is the person who runs fastest in it. By contrast, in long jump people are given a number of jumps and their score is the maximum distance out of all of the attempts. To illustrate, suppose Bunny had the following three attempts: 1.9 meters, 0.32 meters (she tripped), and 2.05 meters. Her score would be the maximum of all of them: 2.05 meters. This is the same score she'd get if her three jumps were 2.01, 2.03, and 2.05. However, if her score were the mean of the three attempts, these two situations would result in very different scores: in the first it would be 1.42 and in the second it would be 2.03. Now, remember that one can have sampling distributions of any kind of statistic. We've spent a lot of time talking about the sampling distribution of the mean, but we could also think about the sampling distribution of the maximum, which applies when thinking about long jump scores. In this problem you will reason about this situation, by direct analogy and extrapolation from what you've learned about the sampling distribution of the mean.