Busy Sally Socialite has trouble remembering people's birthdays, so she has organised her friends into what she calls a Birthday Support Team, or BST. Each friend needs only to keep track of three items of information: their own birthday (which of course they do not need to write down), the name of someone whose birthday comes earlier in the year than their own (which they write on a card and keep in their left pocket), and the name of someone whose birthday comes later in the year (which they write on a card and keep in their right pocket).

Whenever Sally makes a new friend, she calls her best friend, who is currently Harry, and initiates an Install New Support Enquiry Response Tag procedure (INSERT for short). If the new friend's birthday is before Harry's own birthday, then he relays the INSERT call to the person whose name is on the card in his left pocket. If the new friend's birthday is instead after Harry's, then he relays the call to the person on the card in his right pocket. However, if the appropriate pocket is currently empty, Harry writes the name on a new card and puts the card in the empty pocket. Of course, the person to whom Harry relays the INSERT does the same thing, which means that collectively the BST ends up remembering the new friend's birthday.

The first thing Sally needs to do every morning is to find out whose birthday it is that day, and the BST again swings into action. Sally calls Harry and initiates the Sudden Enquiry Activity Requiring Collective Help procedure (SEARCH for short). If the day in question happens to be Harry's own birthday, he tells Sally the happy news and hangs up. Otherwise, he will need to consult with his friends. If Harry has not yet celebrated his own birthday this year, he calls the person on the card in his left pocket to ask whose birthday it is, then relays the answer back to Sally. If Harry's birthday has already passed, he calls his right-pocket friend instead. In either case, if the appropriate pocket is empty, he can tell Sally that it is nobody's birthday. Of course, whoever Harry calls will follow the same procedure so that, collectively, the BST will either provide the name of the birthday celebrant or discover that nobody is celebrating a birthday that day.

For example, if Sally calls Harry on 30 June and asks ‘Whose birthday is it today?’, Harry would reach into his right pocket then put Sally on hold and call Marge. Marge would find John's name in her left pocket then put Harry on hold and call John. Finally, John would report that it is his birthday, which Marge would relay back to Harry, who in turn would report to Sally. Of course, Sally would then call John to wish him ‘Happy Birthday’.

Further explanation Of course, a “Birthday Support Team” is really just a thinly disguised Binary Search Tree, when we look at the details of how it works. Each friend in the “Team” can be represented by a node in a Binary Search Tree, and the left and right “pockets” correspond to left and right branches from that node to other nodes. The ordering of friends that is imposed by the Binary Search Tree is according to the order of the days of the year, with birthdays that occur earlier in the year going to the left subtree below a particular node, and birthdays that occur later in the year going to the right subtree. All of the questions in this Report pertain to a Binary Search Tree solution for the problem.

Task

1. The main problem is that as Sally's circle of friends grows, it sometimes takes a long time to get a response to SEARCH calls, which is using up valuable talk-time on Sally’s mobile phone plan.

• Explain the circumstances that would result in unnecessarily long SEARCH calls and what can be done to minimise the problem.

• If on average a SEARCH call takes one minute — deciding who to call, placing the call, and reporting its outcome — what is the maximum time that a SEARCH might take if Sally added all 180 of her friends to her BST?

• If the problem could be fixed, how much time would a typical SEARCH take?

Further Explanation: This question has to do with the performance of a binary search tree, i.e. the time that it takes to perform specific operations. Explain under what circumstances the long waiting times for search operations would occur, and how these waiting times can be reduced. Explain the maximum waiting time if the problem has not been fixed, and the typical waiting time if the problem can be fixed in the way you have described. You will receive a better mark if you don’t just state the numeric answer, but also explain your reasoning.

2. Knowing that Sally's BST could become inefficient, you have devised a Repair Over-Time Acknowledgement To Enquiries procedure (ROTATE for short), which Sally can use to rearrange friends in the BST. The procedure comes in two variations: ROTATE-L and ROTATE-R.

You have drafted the following email, which Sally can send to people who need to use the ROTATE-L procedure to change one of their friends. If she needs someone to use the mirror-image ROTATE-R procedure, she would substitute the words in bold with the words in parenthesis.

Dear
My BST needs reorganisation, and I need your help. Please call the friend I have asked you to change and pass on the following instructions:

‘Call your right-pocket (left-pocket) friend, ask them the name of their current left-pocket (right-pocket) friend, and tell them to replace that name with yours. Then tell me your friend's name and replace their name on the card in your pocket with the one they reported to you.’

When you have finished the call to your friend, replace their name on the card in your pocket with the name they reported.

Sally has sent you a record of the order in which she INSERT-ed friends into her BST. (Note that in this case, Hananah starts out being the best friend, as she is added first. The best friend will not necessarily be the same person throughout the lifetime of the BST.)

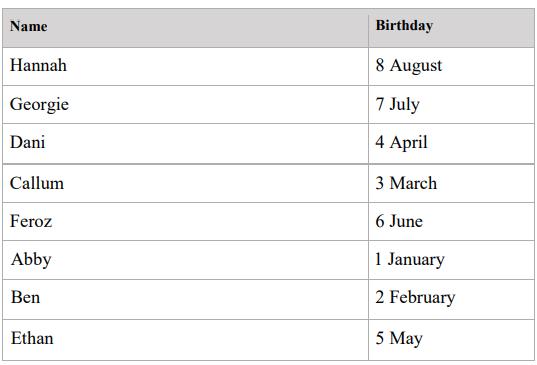
Draw a diagram of Sally's current BST and compile a list of the sequence of ROTATE emails Sally would need to send in order to reorganise the BST so that subsequent SEARCH times are minimised. You don’t need to include the full text of the emails, but your list should indicate who to send the email to, which friend needs to be changed, and which form of ROTATE to use. Include intermediate diagrams showing the effect of each rotation on the BST. Note that it may be necessary for Sally herself to change her best friend using a ROTATE.

Further Explanation: These operations correspond to the standard rotate operations that are defined for a binary search tree. For this question and also the next one, you are asked to create diagrams to illustrate what happens as the tree is rotated. These diagrams do not need to be created with software; images/photos of neat hand-drawn diagrams are fine.

Name Hannah Georgie Dani Callum Feroz Abby Ben Ethan Birthday 8 August 7 July 4 April 3 March 6 June 1 January 2 February 5 May