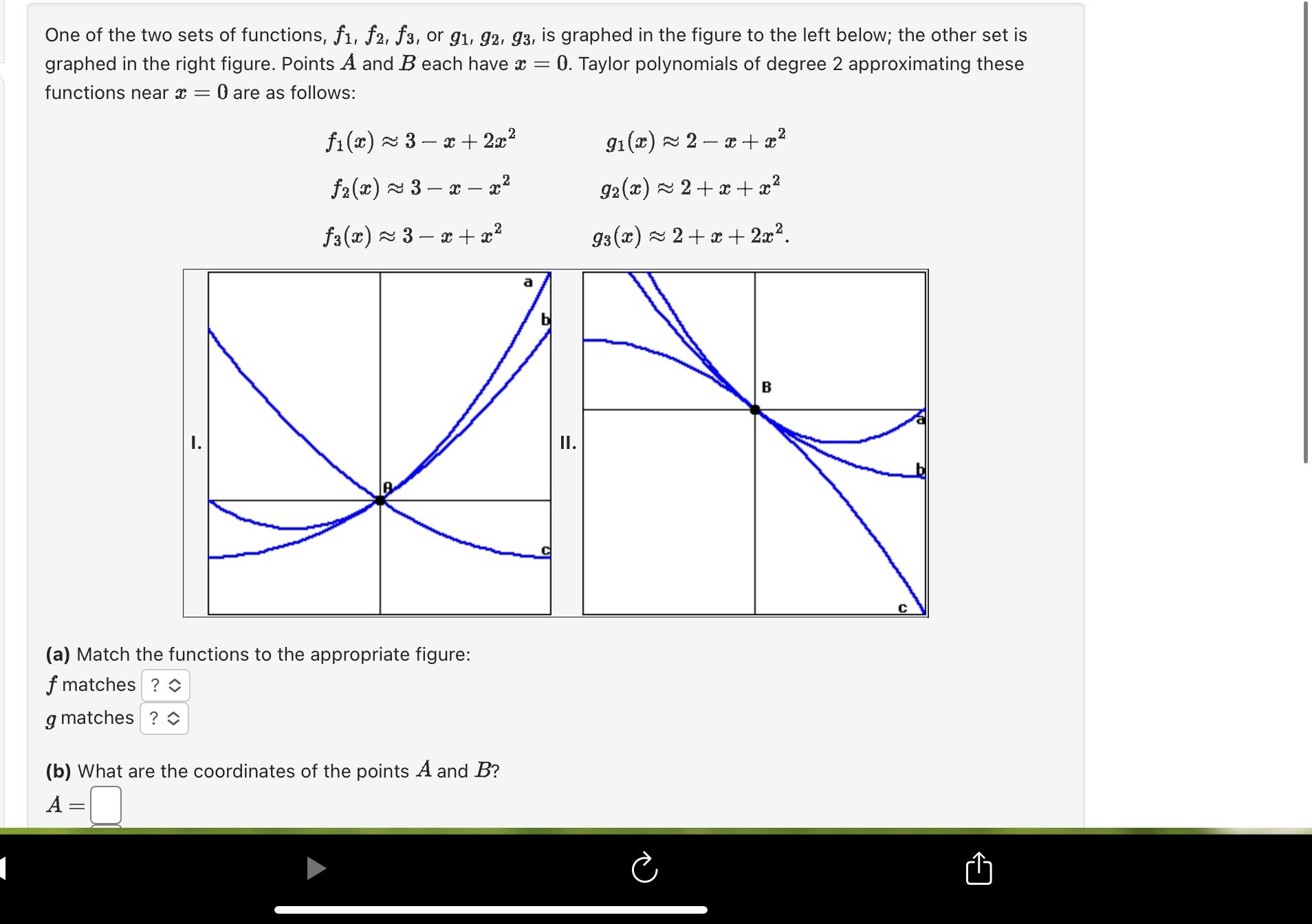
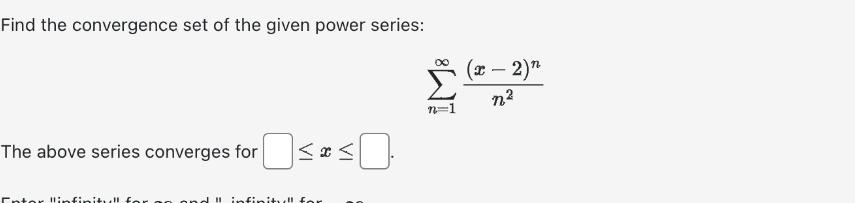
By recognizing each series below as a Taylor series evaluated at a particular value of x, find the sum of each convergent series. A. 1 + + ( ) 2 + () + () + + () + : B. 1+7+ + Find the interval of convergence for the given power series. The series is convergent from x = to x = left end included (enter Y or N): right end included (enter Y or N): n=1 (x - 10)" n(-9)n Suppose that you are told that the Taylor series of f(x) = x ex about x = 0 is Find each of the following: () dx d" da7 (*) 2=0 = x3 + + + + x 11 + 2! 3! 4! Let Coc(ra) + c (x a) + ... + Cn(x - a)" be the Taylor series of the function f(x) = x sin(x). - For a 0 determine the value of C3. C3= Find all the values of x such that the given series would converge. (-1)"x" 3" (n+8) The series is convergent from x to x = left end included (enter Y or N): , right end included (enter Y or N): One of the two sets of functions, f1, f2, f3, or 91, 92, 93, is graphed in the figure to the left below; the other set is graphed in the right figure. Points A and B each have x = = 0. Taylor polynomials of degree 2 approximating these functions near x = 0 are as follows: f1(x) 3 - x+2x 91(x) 2 -x+x 2 f2(x) 3 x x 92(x) 2+x+x f(x) 3-x+x 2 93(x) 2+x+2x. I. II. (a) Match the functions to the appropriate figure: f matches ? g matches? (b) What are the coordinates of the points A and B? A B Find the convergence set of the given power series: The above series converges for x Enter infinityll for on "infinitu!! for 0 (x - 2)" n2