By showing (a) through (c), prove EX( )2 2(p + 1). Prove the following statements: (a) For covariates x1,...,xN , if we obtain

By showing (a) through (c), prove EX(β˜ − β)2 ≥ σ2(p + 1).

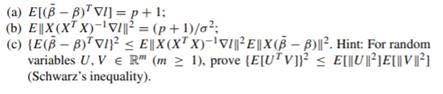
Prove the following statements:

(a) For covariates x1,...,xN , if we obtain the responses z1,...,zN , then the likelihood

of the parameter γ ∈ Rp+1 is

for an arbitrary β ∈ Rp+1

(b) If we take the expectation of (a) w.r.t. z1,...,zN , it is

(c) If we estimate β and choose an estimate γ of β, the minimum value of (b) on average is

and the minimum value is realized by the least squares method.

(d) Instead of choosing all the p covariates, we choose 0 ≤ k ≤ p covariates from p. Minimizing

w.r.t. k is equivalent to minimizing N log σ2 k + k w.r.t. k, where σ2 k is the minimum variance when we choose k covariates.

(a) E[(8-8)TVI] = p + 1: (b) EX(X7 X)-V/ = (p+1)/0; (c) (E(B-B) VI variables U. V (Schwarz's inequality). EX(XX)-VIE ||X (B-B). Hint: For random R (m 1), prove (E[UTV] E[U]E[V]