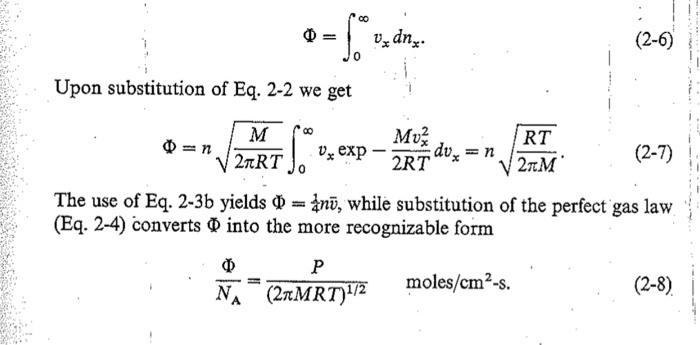c. In terms of deposition of films, we are often concerned about the flux of atoms colliding with the surface, as given by equations 2-7 to 2-9. i. Is equation 2-7 or 2-8 composed of purely extensive measurements? ii. Explain why the measurements in 2-7 or 2-8 easier to make. iii. Rewrite equation 2-9 in terms of atmospheres iv. Using the above rewrite equation 2-11 in terms of atmospheres So , V dne (2-6) Upon substitution of Eq. 2-2 we get M 270RT vx exp Muz 2RT dux =n RT 21M (2-7) The use of Eq. 2-3b yields 0 = 4n7, while substitution of the perfect gas law (Eq. 2-4) converts into the more recognizable form P NA (2MRT)12 moles/cma-s. (2-8) A useful variant of this formula is P 0 = 3.513 x 1022 molecules/cma-s (2-9) (MT)1/2 when P is expressed in torr. As an application of the preceding development, consider the problem of gas escaping the vessel through a hole of area A into a region where the gas concentration is zero. The rate at which molecules leave is given by A and this corresponds to a volume flow per second () given by A cm/s. Upon substitution of Eqs. 2-4 and 2-9, we have V = 3.64 x 10%(T/M)*2 A cm/s. (2-10) For air at 298 K this corresponds to 11.7A liters/s, where A has units of cm? In essence we have just calculated what is known as the conductance of a circular aperture, a quantity that will be utilized later because of its significance in pumping gases. As a second application, consider the question of how long it takes for a surface to be coated by a monolayer of gas molecules. This is an issue of great importance when attempting to deposit or grow films under extremely clean conditions. The same concern arises during surface analysis of films, which is performed at very low pressures in order to minimize surface contamination arising from the vacuum chamber environment. Here one must make certain that the analysis time is shorter than that required for impurities to accumulate. This characteristic contamination time, te, is essentially the inverse of the impingement flux. Thus, for complete mono- layer coverage of a surface containing some 1015 atoms/cm, the use of Eq. 2-9 yields 1045 (MT)/2_2.85 x 10-8 t. (MT)/2 s, (2-11) 3.513 x 1022P P with P measured in torr. In air at atmospheric pressure and ambient temperature a surface will acquire a monolayer of gas in 3.49 X x 10-s assuming all impinging atoms stick. On the other hand, at 10-10 torr a surface will stay clean for about 7.3 h. Surface exposure to gases is measured in Langmuir (L) units of pressure-time, e.g., torr-s. The conversion is 1L = 10-6 torr-s, which means gas exposure could occur at 10- torr for 1s, at 10-7 torr for 10 s, etc. Therefore, since a monolayer typically forms after 7.3h (26,280 s) at 10-10 torr (or 2.63 L), 1 Langmuir corresponds to about 0.38 monolayer